統計や機械学習でよく使うデータ分析手法５選【初心者必見】

データ分析初学者の方で、データ分析の学習を進めていくと

と思っている方が多いのではないでしょうか。今回はそんな方に向け、データ分析手法で押さえておくべき手法5選を紹介していきます。

なお、本記事はデータ分析手法をこれから学ぶ方に向けて書いていますので、分析方法とその考え方を紹介し、細かい計算等は省きます。

データ分析手法とは

実務で扱うデータは統計的にどのような特徴を持っているかは全く不明です。しかも、場合によってはまったく意味のないデータが紛れていることもあります。このデータを様々な手法でどのようなものかを分析していくにあたり、よく使用する手法を紹介します。

以下の記事では機械学習を実施する前にデータの素性を調べることの重要性を紹介しています。

【１分でわかる】特徴量エンジニアリングの進め方機械学習でモデル精度を上げようとすると突き当たる特徴量エンジニアリング。重要であることは理解できるけどなんで？またどうしたらいいの？という疑問に答えていきたいと思います。...

データ分析手法５選

今回紹介する手法は以下の５つです。「分散分析」など重要な考え方もありますが、上の項目から順番に学習していくと使用範囲も多いのでよいでしょう。

手法	概要と使用シーン
相関分析	二つのデータ間の関係性を分析します。二変数間の関係性を確認することにより説明変数を採用するのか、加工しないといけないのかを検証します。
回帰分析	データの関係を「y=ax+b」などの式の形で表現できないかを検討します。関係性を分析できると未知の情報に対しても答えを予測することができるようになります。
主成分分析	データが持っている情報を最もよく表している軸を探すことにより、データが持っている情報を探し出したり次元を削減することができます。
クラスター分析	データの塊を検証することにより、データの塊具合を検証します。これによりデータの特性や、層別の必要性を検証できます。
分散分析	「データのばらつき＝変動の大きさ」を検証することにより有効な説明変数を検証します。

データの関係性を確認「相関分析」

相関分析とは

2つの変数間の統計的な関連性を指します。これは、一方の変数が変化するときに、「他方の変数がどのように変化するか」と「関連性がどの程度あるか」を示します。

この関連性の度合いを「相関係数」と呼び、ー１から１の数値で表します。相関係数は下記のような状態を示します。

なお、これは数値的に相関があるだけで、因果関係があるかどうかはわかりませんので注意が必要です。

なぜ相関分析を行うのか

この相関分析によって、「目的変数と関連の大きそうな説明変数を見つけたり」、「説明変数間の関連性や、項目間の関連性がどの程度あるかを確認したり」することが可能です。

説明変数同士の相関が高いと解析結果が不安定になるため、必ず実施すべき分析の一つです。

このような理由で結果が正しくでない、不安定になる場合は、説明変数を削減したり必要に応じて説明変数をまとめて新たに説明変数を作成する必要があります。

データをモデル化「回帰分析」

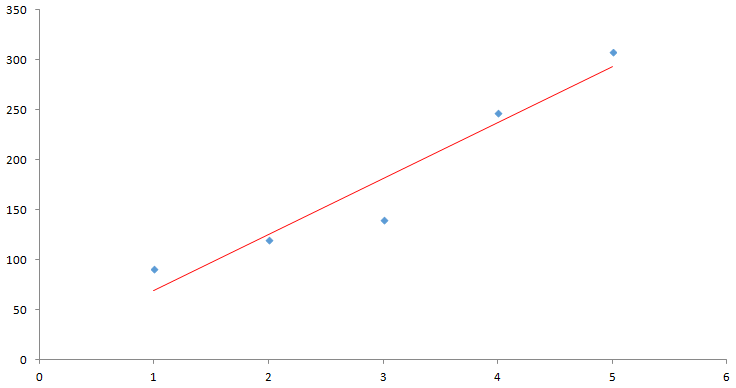
回帰分析とは

回帰分析はデータの入力に対して関係をモデル化し、その結果を予測する方法です。上図では、赤い線のような「y=ax+b」の形で予測する単回帰分析を行っています。

回帰分析は上図のように単純な単回帰分析、複数の項目から結果を予測する重回帰分析、結果をロジット変換してわかりやすくするロジスティック回帰、そのほかリッジ回帰などがあります。

以下の記事ではロジスティック回帰について解説しています。

【1分でわかる】ロジスティック回帰とは？理論や算出方法をわかりやすく解説！ロジスティック解析とはよく聞く名前ですが、いったいどういうものか、何をしているのかを統計がわかっていないかたへもわかりやすく解説していこうと思います。オッズ比や重回帰分析、確率の算出を行います。実際にコードを示しながら進めているので、一緒に手を動かしながら学べます！...

なぜ回帰分析を行うのか

回帰分析で解決できる問題は式に当てはめることで結果がわかるように、非常に説明性が高く、非常に扱いやすいくなります。また、結果に対する原因の影響力の大きさがわかるため、結果を改善したい場合の対策が見えやすいという長所があります。

データを要約「主成分分析」

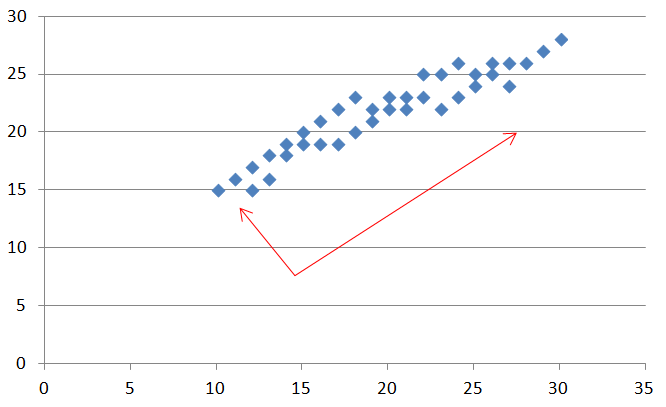
主成分分析とは

主成分分析は既存の軸から新たな軸を探し出すことにより、

ことが可能です。主成分分析の意味や実施方法については以下の記事を参照してください。

【1分で理解】Pythonでの主成分分析の方法を解説！グラフ化で特徴把握PythonのSklearnを使用して、主成分分析を行って情報を二次元グラフに落とし込んで画像で見えるようにします。寄与率に関しても確認方法を見ていきましょう。...

なぜ主成分分析を行うのか

主成分分析は主に次元を削減するために使用します。次元の削減とは、説明変数の数を減らすことにより少ない変数で目的変数を説明することです。次元を減らすことで、計算時間短縮や、人が理解しやすい２次元の散布図にしてデータ全体の傾向を把握したりするために使用します。

特にデータ解析の手始めに、次元削減をして全体のイメージをつかむことはデータ分析の取り掛かりとして非常に有用な方法になります。

データの散らばりを確認「クラスター分析」

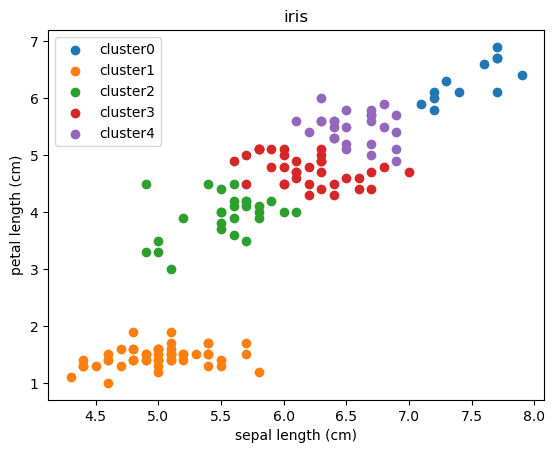
クラスター分析とは

クラスターとは「群、集団、塊」などを示す語で、データの塊を指します。クラスター分析は、その名の通りデータをクラスターに分割します。具体的な手法には、K-meansや階層的クラスタリングがあります。

以下の記事ではクラスター分析について解説しています。

クラスタリングをPythonで！K-meansの解説から実装までクラスタリングといえばK-meansを思い浮かべることも多いと思います。K-meansってなに？という内容から、K-measnsの実装・手法、そのほかのクラスタリング（階層的クラスタリング・非階層的クラスタリング）までわかりやすく解説しています。...

なぜクラスター分析を行うのか

意味のあるデータのかたまりを見つけ出すために、まずはクラスター分析をしてクラスターを見つけ出すことはよく行われます。

データを分析する際、違う特性に従っているデータが混ざっているとそこに意味を見出せなくなります。したがって層別することは非常に重要な作業になります。

その層別のまとまりを見つけるための手がかりとしてまずはクラスター分析を行い、そもそも層別する必要があるのか、どのように層別するのかを検討します。

基本となる考え方「分散分析」

ここまでいくつかの分析方法を紹介しましたが、分析手法の多くで元となっている考え方「分散分析」を見ていきましょう。細かく確認すると理解しにくい部分もあるので、ここでは考え方のイメージをつかんでください。

分散分析とは

群間の母平均の差を検定する分析です。「各群の母平均は等しい」かどうかをF検定を行って検定します。F値が閾値以上の場合、先ほどの「母平均は等しい」ということを否定し、それぞれの群に意味がある、つまり先ほど考えた要因は誤差と違うものなので意味があるものだ、ということを考えます。

分散分析で行っていること

ある点を測定した場合、その点がどのような法則に従って現れるかを考えてみます。今回はわかりやすく１点で考えていますが、実際には複数点を取って解析します。まずはイメージをつかんでください。

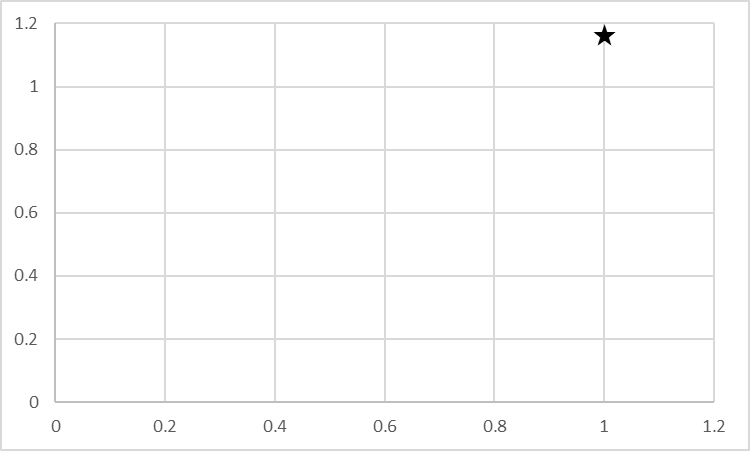
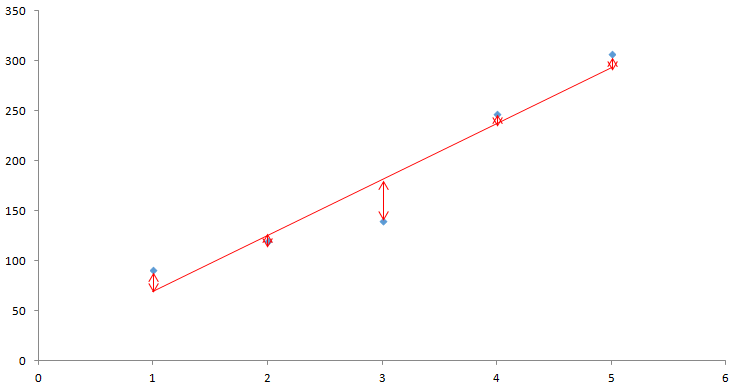
ある１点を上記の星印で観測したとします。

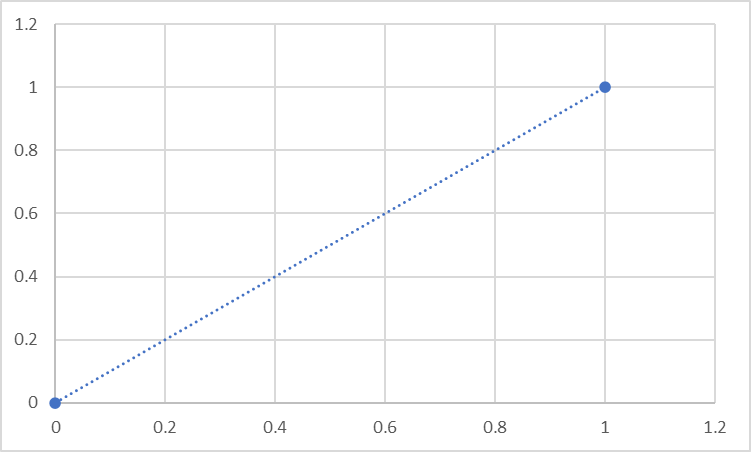
これが上記のような式、この場合ｙ＝ｘに従っているとします。

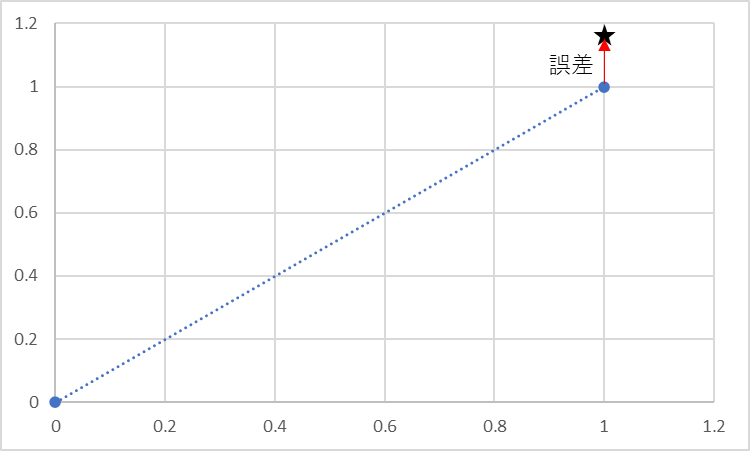
しかし、実際に測定する際にはｙ＝ｘの直線上で観測されることは少なく、そこには測定誤差や環境による誤差、そのほかいろいろな誤差が含まれています。上の図で見ると、本来出てくる点に誤差を加えたものが実際の測定点となるわけです。

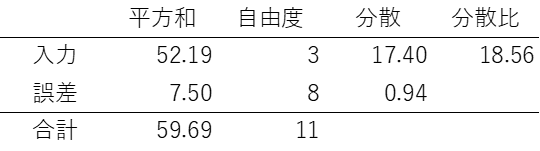
では、実際の分析です。実際の分析では上のような平方和、自由度、分散を表にしたものを使用します。これは、入力による分散と誤差による分散、すなわち入力によって動くデータの量と誤差によって動くデータの量を比較し統計的に「平均は誤差と同じか？」を分析するものです。

この分散比がF値より大きければ「誤差と同じである可能性は低いよね」つまり誤差と同じではないので影響がある、という考え方です。

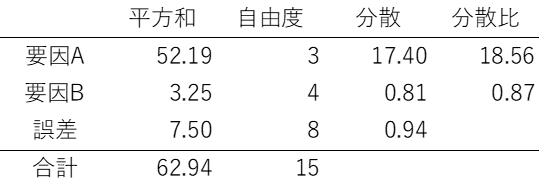
これと同じようにいくつかの要因がある場合にも、それぞれの要因が誤差なのか、意味のある要因なのかを分析することが可能です。

【コラム】誤差と同じかどうか、ということ

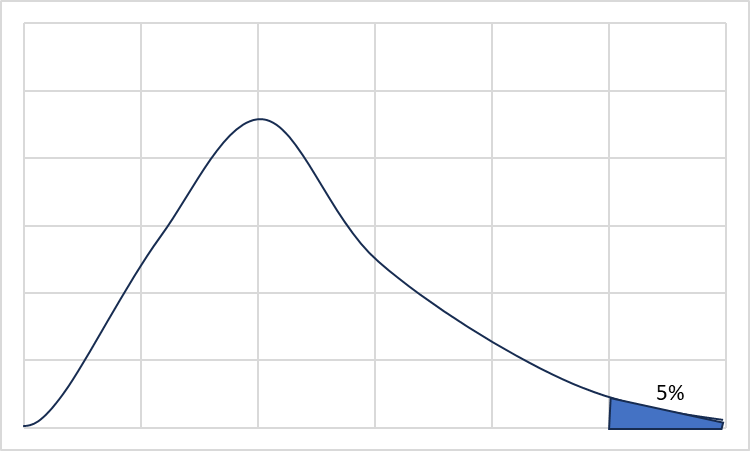
先ほど「F値より大きければ誤差とは別もの」と簡単に書きましたが、分散分析で最終的に行っていることは誤差とのF検定です。

冒頭にも書きましたが、「母平均は同じものである」というところを出発点にし、F検定によって「同じである確率は５％以下だから統計的にべつものだ」という考え方をしています。

以下の記事では「分散分析」と同様の考え方で、本来の数式を求める方法として最小二乗法を解説しています。

１からわかる！最小二乗法とエクセルlinest関数を理解するエクセルで最小二乗法を使用して単回帰分析したい方へ、その方法をわかりやすく解説します。関数で解決するためのlinest関数の使い方、そして関数を使わない簡単な方法も考えてみます。...

その他確認すべき分析方法

決定木分析

木構造でデータを分析していく方法。わかりやすさと精度の高さ、計算の速さで非常に扱いやすい分析手法です。

以下の記事で決定木のやり方について解説しています。合わせて参照してください。

【1分でわかる】初心者でも簡単にPythonで決定木の実装ができるやり方を学ぶ！機械学習の基礎である決定木を、概要の解説からPythonで初心者でも簡単に実装する方法、結果の表示のやり方までわかりやすく解説していきます。また、graphvizで表示する方法まで合わせて解説しています。本記事により適切に決定木を用いてデータの分析に役立てていただければと思います。...

まとめ

今回は統計解析や機械学習で使用されるデータ分析手法を解説しました。どのようなものがあるかを理解しておくことで、分析時の武器が増えますので一通り理解しておきましょう。詳細な使用方法はその都度確認すればよいので、まずはどのようなものがあるかを理解しておくことが重要です。