連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第6章では、「代表的な確率分布」について解説します。
分布の形からそれぞれの分布の期待値など詳細に解説しているので、ぜひご覧ください。
また、以下の記事ではエクセルで確率分布を使用する方法を紹介しています。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章：平均・分散などの基本統計量
2章：相関関係
3章：確率の基本
4章：条件付き確率・ベイズの定理
5章：期待値
6章：代表的な確率分布
7章：母集団と標本
8章：標本平均・不偏分散
9章：中心極限定理
10章：母平均の推定(分散既知)
11章：母平均の推定(分散未知)
12章：仮説検定
13章：正規分布を用いた検定
14章：【t検定】母平均を検定
15章：【F検定】分散に差があるか？
16章：ウェルチの検定
17章：カイ2乗検定
18章：分散分析
19章：回帰分析
本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。
確率分布とは
確率分布について紹介する前に、「確率変数」という言葉について確認しておきましょう。
変数Xがとりうる各値に対して確率が与えられている時、Xを確率変数と言います。
例えば、サイコロの確率変数Xは「1から6までの整数の値を取る変数」となります。
次に確率分布の定義を説明します。
確率分布とは、確率変数のそれぞれの値の確率を関数として表したものです。
本記事の「確率分布」は、確率変数に対して確率を対応させる関数である確率密度関数を表しています。
確率変数がある値以下を取る確率を示す関数である累積分布関数とは異なるので注意しましょう。
例として、サイコロの出る目の確率はそれぞれ「1/6」なので確率分布は以下のように表せます。
$$
f(X = x) = \frac{\scriptsize 1}{\scriptsize 6} \quad(x = 1,2,3,4,5,6)
$$
また、この確率分布のグラフは次のようになります。
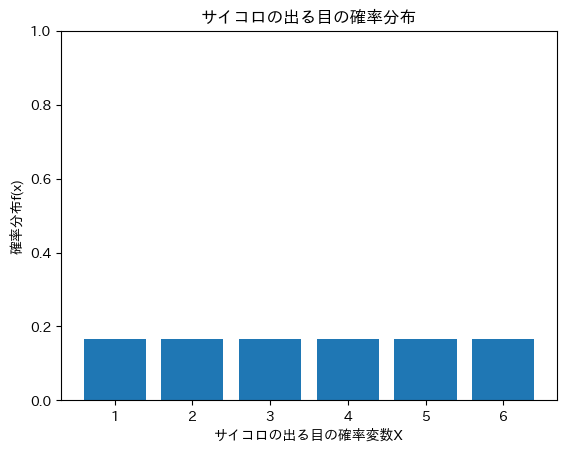
離散型確率分布
離散型確率分布とは、確率変数Xが離散型である場合の確率分布のことを指します。
離散型というのは、飛び飛びの値を取ることを意味します。
例えば、サイコロの目は、「1」、「2」、…というように飛び飛びの値を取ります。
それでは、代表的な離散型確率分布について紹介していきます。
一様分布
一様分布とは、N個の事象が等確率で起こる場合の分布です。
一様分布の確率分布の式は一般に次のように書けます。
$$
f(X = x) = \frac{\scriptsize 1}{N} \quad(x = 1,2,3,…,N)
$$
上記で紹介した「サイコロの出る目の確率分布」は一様分布に該当します。
また、期待値と分散も確認しておきましょう。
期待値について詳しく知りたい方は下記の記事をご覧ください。
分散について詳しく知りたい方は下記の記事をご覧ください。
期待値
$$ E(X) = \frac{N+\scriptsize 1}{\scriptsize 2} $$
分散
$$ V(X) = \frac{N^{\scriptsize 2} – \scriptsize 1}{\scriptsize 12} $$
二項分布
次に「二項分布」という確率分布を紹介しますが、二項分布を理解するために「ベルヌーイ試行」について解説します。
ベルヌーイ試行
ベルヌーイ試行とは、「成功」と「失敗」のように、「事象A」と「その余事象」の2つの事象しか持たない試行を指します。
ベルヌーイ試行の例として、以下のような場面があります。
- コインを投げて「表」が出るか、「裏」が出るか
- サイコロの出目が「偶数」か「奇数」か
- 野球において、「出塁する」か、「アウトになる」か
また、成功をx = 1、失敗をx = 0とし、各々の確率を「p」,「1−p」と定義する場合が多いです。
例えば、コインを投げる場合
- 表が出る → 成功 →「 x = 1」
- 裏が出る → 失敗 →「 x = 0」
という風に設定します。
もちろん、「成功」と「失敗」を逆に定義しても構いません。
ベルヌーイ試行において、期待値と分散は以下のようになります。
期待値
$$ E(X) = p $$
分散
$$ V(X) = p({\scriptsize 1}-p) $$
二項分布
次に本題の二項分布について解説していきます。
二項分布とは、n回のベルヌーイ試行を繰り返したとき、事象Aの起こった回数Xが従う確率分布です。
例えば「コインをn回振って、x回表が出る確率」などを考えると、この二項分布が現れます。
ここで、二項分布で登場した文字について確認しておきます。
| p | 事象Aが起こる(成功する)確率 |
|---|---|
| n | 試行回数 |
| x | 事象Aの起こった(成功した)回数 |
二項分布の確率分布の式は一般に次のように書けます。
$$ f(X = x) = {}_n C_k \cdot p^x \cdot ({\scriptsize 1} – p)^{n-x} \quad (x = 1,2,\ldots, N) $$
「確率の計算の仕方」や「C」について詳しく知りたい方は下記の記事をご覧ください。
また、試行回数が「n回」、事象Aが起こる(成功する)確率が「p」の二項分布は
$$ Bi(n,p) $$
と表します。
したがって、ベルヌーイ試行は
$$ Bi({\scriptsize 1},p) $$
と書けます。
試行回数が100回(n=100)、事象Aが起こる確率(成功確率)が0.3(p=0.3)の場合、二項分布のグラフは下記のようになります。
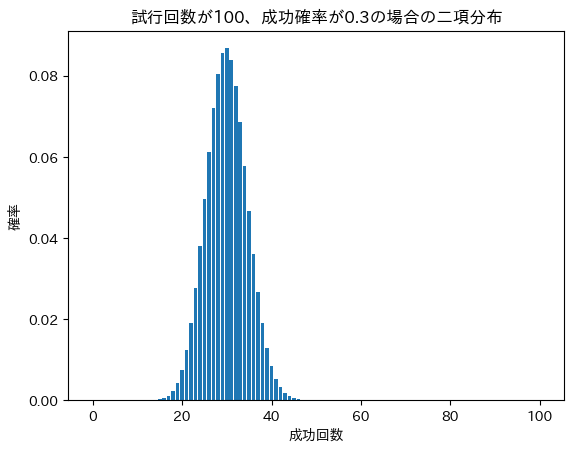
グラフより「成功する確率が30回に近いほど高い」と読み取れます。
二項分布において、期待値と分散は以下のようになります。
期待値
$$ E(X) = np $$
分散
$$ V(X) = np({\scriptsize 1}-p) $$
ポアソン分布
ポアソン分布は、単位時間あたり平均u回起こる事象がx回起こる確率を表します。
ポアソン分布の確率分布の式は次のように書けます。
$$
f(X = x) = \frac{u^x \cdot e^{-u}}{x!} \quad(x = 1,2,3,…,N)
$$
なお、「e」はネイピア数と呼ばれ、
e = 2.71828182845904523536……
と無限に続く値をもちます。
ポアソン分布の具体例について確認しましょう。
具体例
1時間に平均5回の電話の着信があるとします。
このとき、ある1時間で電話の着信が10回ある確率を求めましょう。
ポアソン分布の定義と照らし合わせると
$$
\begin{align*}
u &= \scriptsize 5\\
x &= \scriptsize 10
\end{align*}
$$
となります。
よって、
$$
\begin{align*}
f(X = {\scriptsize10}) &= \frac{\scriptsize 5^{\scriptsize 10} \cdot e^{\scriptsize -5}}{{\scriptsize 10}!}\\
&\simeq \scriptsize 0.018
\end{align*}
$$
ポアソン分布のグラフの形は以下のようになります。
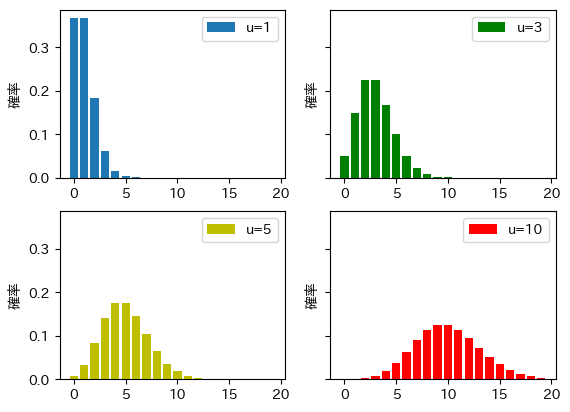
2項分布において、平均値「μ=np」を固定して「n→♾️」、「p→0」のときの分布を考えるとポアソン分布を導出することができます。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
連続型確率分布
連続型確率分布とは、確率変数Xが連続型である場合の確率分布のことを指します。
離散確率分布はf(x)が「xが起こる確率そのもの」を表しているのに対して、連続確率分布はf(x)の積分により「xが積分範囲内の値である確率」を表しています。
例えば、「身長」や「温度」といった確率変数を考えると連続型確率分布になります。
連続型確率分布のグラフの概形について確認しましょう。
下記の図のように、確率変数Xが連続の値をとります。
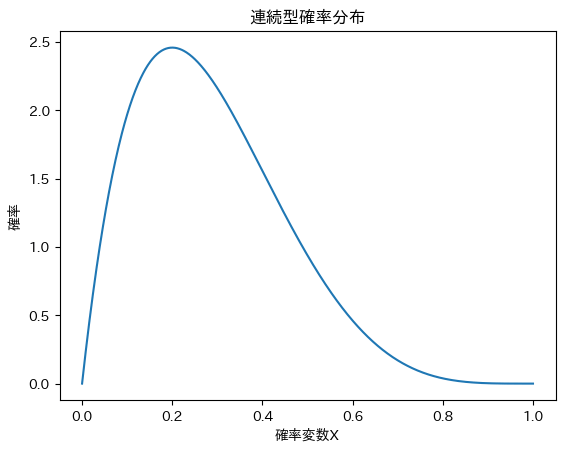
それでは、代表的な連続型確率分布について紹介していきます。
正規分布
正規分布は、その形状が左右対称で、中央部分が高く、両側に裾が広がっている特徴的なベル型の曲線で表されます
また、正規分布はガウス分布と呼ばれることもあるので注意しましょう。
正規分布は確率・統計において最も頻出し、重要である確率分布なので、その特徴をしっかりと理解しましょう。
正規分布の確率分布の式は次のように書けます。
$$
f(X = x) = \frac{\scriptsize 1}{\sqrt{{\scriptsize 2}\pi \sigma^{\scriptsize 2}}} \cdot e^{-\frac{(x – u)^2}{{2\sigma^2}}}
$$
ポアソン分布と同様に、
e = 2.71828182845904523536……
を表します。
また、\(e^x\)を\(\scriptsize \exp(x)\)と表すことも多いです。
$$
f(X = x) = \frac{\scriptsize 1}{\sqrt{{\scriptsize 2}\pi \sigma^{\scriptsize 2}}} \cdot \exp{({-\frac{(x – u)^2}{{{\scriptsize 2}\sigma^{\scriptsize 2}}})}}
$$
- uは平均値
- σは分散
を表します。
また、
正規分布のグラフの形は以下のようになります。
(u = 0, σ = 1)
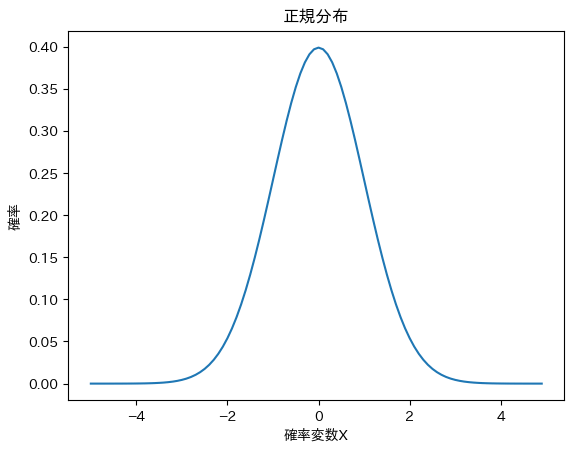
正規分布の特徴として主に以下の2つが挙げれれます。
- 平均値、最頻値、中央値が一致する。
- 母集団の分布が、例外を除いてどんな分布であっても、標本の大きさを大きくしたとき、標本平均の分布は近似的に正規分布に従う。(中心極限定理)
中心極限定理は、基本的に母集団がいかなる分布に従っていても使うことができる汎用性が高い定理のため、統計学では正規分布がとても重要な役割を果たしています。
平均値や最頻値などの基本統計量について詳しく知りたい方は以下の記事をご覧ください。
また、中心極限定理は第10章で詳しく解説しているのでそちらもご覧ください。
中心極限定理のイメージやメリット、さらに中心極限定理が成り立たない例外の分布まで詳しく解説しています。
正規分布において、期待値と分散について確認しておきましょう。
期待値
$$ E(X) = u $$
分散
$$ V(X) = \sigma^{\scriptsize 2}$$
指数分布
指数分布とは、単位時間あたり平均λ回起こる事象の発生間隔がx単位時間である確率密度を表しています。
指数分布の式は次のように書けます。
$$ f(X = x) = x \cdot e^{- \lambda x} $$
少し表現が難しいと思うので具体的な例で確認しましょう。
具体例
Aさんの携帯には、1日で平均2回のメールが入ってくるとします。
この時「メールが入ってくる」という事象の起こる間隔がx日である確率を指数分布は表しています。(単位時間は「日」)
すなわち、3日ちょうどでメールが入ってくる確率密度は
$$ f(X = \scriptsize 2) = {\scriptsize 3} \cdot e^{- \scriptsize 2 \times \scriptsize 2 } $$
多くの場合はx単位時間以内に事象が起こる確率を知りたいと思います。
x単位時間以内で事象が起こる確率は積分により求めます。
$$
\begin{align*}
F(X) &= \int_{\scriptsize 0}^{x} f(x) dx \\
&= \lambda \int_{\scriptsize 0}^{x} e^{- \lambda x} dx\\
&= \scriptsize 1 – e^{- \lambda x}
\end{align*}
$$
したがって、「具体例」において3日以内にメールが来る確率は
$$ \scriptsize 1 – e^{- \scriptsize 2 \times \scriptsize 3} \simeq \scriptsize 0.998 $$
と求められます。
指数分布の形は以下のようになります。
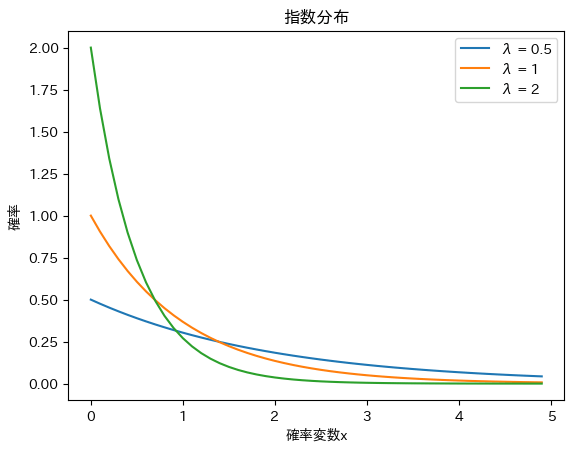
指数分布において、期待値と分散について確認しておきましょう。
期待値
$$ E(X) = \frac{\scriptsize 1}{\lambda} $$
分散
$$ V(X) = \frac{\scriptsize 1}{\lambda ^{\scriptsize 2}}$$
