連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第8章では、「母平均・母分散の点推定」について解説します。
平均・分散の点推定や「標本分散」と「不偏分散」の違いなどを分かりやすく解説しているので、ぜひご覧ください。
本格的な統計学の内容に入っていくので、「母集団」や「標本」などの基本用語を確認したい方はこちらの記事をご確認ください。

本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章:平均・分散などの基本統計量
2章:相関関係
3章:確率の基本
4章:条件付き確率・ベイズの定理
5章:期待値
6章:代表的な確率分布
7章:母集団と標本
8章:標本平均・不偏分散
9章:中心極限定理
10章:母平均の推定(分散既知)
11章:母平均の推定(分散未知)
12章:仮説検定
13章:正規分布を用いた検定
14章:【t検定】母平均を検定
15章:【F検定】分散に差があるか?
16章:ウェルチの検定
17章:カイ2乗検定
18章:分散分析
19章:回帰分析
復習:平均と分散
まず「平均」について確認しましょう。
「全てのデータの値を足し合わせた合計を、データの個数で割って算出される平均値」を算術平均と言います。
n個のデータがあるとき、算術平均は以下のような式で定義されています。
\begin{align*}
\bar{x} &= \frac{x_1 + x_2 + \ldots + x_n}{n} \\
&= \frac{\scriptsize 1}{n} \sum_{i=1}^n x_i
\end{align*}
次に「分散」について確認します。
分散は「データの散らばり具合を表す値」です。
分散は、データの値と平均値の差の二乗の平均で求めることができます。
n個のデータがあるとき、分散は以下のような式で定義されています。
$$ s^2 = \frac{\scriptsize 1}{n} \sum_{i=1}^n (x_i – \bar{x})^2 $$
「平均」や「分散」、その他の統計量の詳しい解説は以下の記事で解説しているのでぜひご覧ください。

復習:点推定とは
点推定とは、母数「\(\theta \)」をただ一つの値「\(\widehat{\theta} \)」で推定する手法を指します。
詳しくはこちらの記事をご覧ください。

点推定には「ベイズ推定」や「最尤推定」など計算が複雑な計算をする推定法もありますが、今回は母平均・母分散を推定するので簡単でイメージしやすい内容となっています。
母平均の点推定
標本平均の定義
標本平均とは、標本データから算出される平均を表します。
標本とは、母集団から分析のために選び出された要素の集団を意味します。
確率変数Xの標本平均\(\bar{X}\)は、通常の算術平均と変わらず
\begin{align*}
\bar{X} &= \frac{X_1 + X_2 + \ldots + X_n}{n} \\
&= \frac{\scriptsize 1}{n} \sum_{i=1}^n X_i
\end{align*}
と求めることができます。
そして、「母平均の推定値」は「標本平均の値」となります。
標本平均のXはどうして大文字なの?
と疑問に思った方に向けて、算術平均と標本平均の間で「小文字」と「大文字」とを使い分けている理由を解説します。
算術平均は、一般にデータ全体の平均(母平均)を求めています。
一方、標本平均は、データから取得された一部のサンプル(標本)の平均を求めています。
そのため、標本平均の値は、母集団からデータを抽出するたびに変わる可能性があり、確率的に値が決まります。
統計学は確率的に決まる値は「大文字」で表し、実数値は「小文字」で表す慣習があります。
母平均の推定例
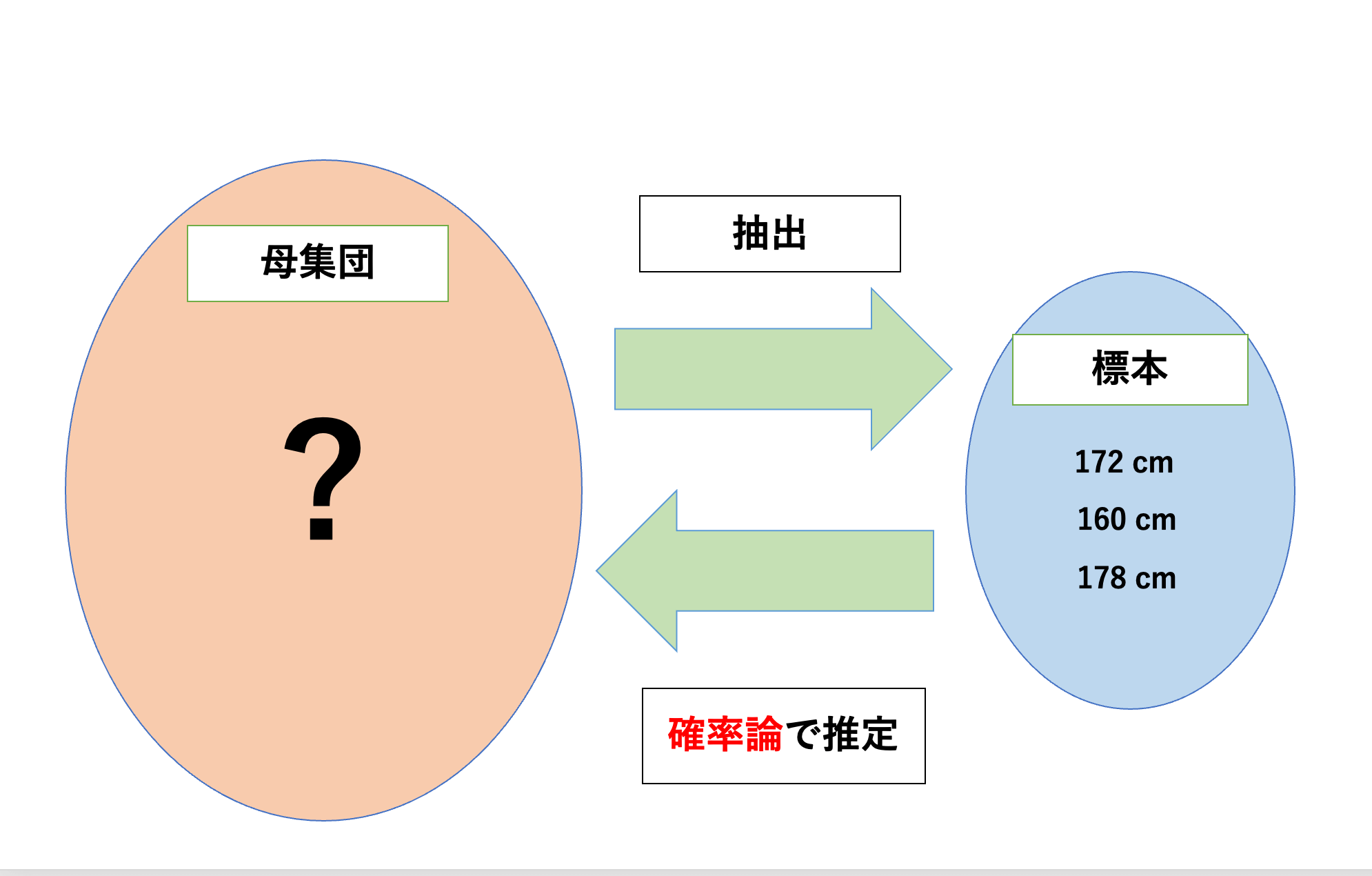
図のように、身長のデータにおいて、母集団から抽出した標本のデータは「170cm」、「160cm」、「178cn」であったとします。
この時、標本平均\(\bar{X}\)は、
\begin{align*}
\bar{X} &= \frac{X_1 + X_2 + \ldots + X_n}{n} \\
&= \frac{\scriptsize 170 + 160 + 178}{\scriptsize 3} \\
&= \scriptsize 170
\end{align*}
と計算できます。
母平均の推定値は標本平均の値なので、母平均の推定値は「170cm」となります。
標本の平均を計算することで、母平均を点推定できるので、母平均の点推定は簡単に行うことができます。
分散の点推定
標本分散とは
標本分散とは、標本データから算出れる分散を表します。
確率変数Xの標本分散\({S^2}\)は、通常の分散と変わらず
$$ S^2 = \frac{\scriptsize 1}{n} \sum_{i=1}^n (X_i – \bar{X})^2 $$
と求めることができます。
母平均の推定とは異なり、母分散の推定値として「標本分散」は不適切とされています。
母分散を推定する際は、次に紹介する「不偏分散」を利用します。
不偏分散とは
不偏分散とは、標本の偏りを除いて母分散をより正確に推定するために用いる分散です。
標本平均は標本の大きさ「n」で割って求めていましたが、不偏分散では標本の大きさ「n」から1を引いた「で割ることで求められます。
すなわち、不偏分散\({U^2}\)は以下の式で求められます。
$$ U^2 = \frac{\scriptsize 1}{n – \scriptsize1} \sum_{i=1}^n (X_i – \bar{X})^2 $$
母分散を推定するときは、この不偏分散を用います。
母分散の推定例

先程と同様に身長のデータにおいて、母集団から抽出した標本のデータは「170cm」、「160cm」、「178cn」であったとします。
母分散の推定値は不偏分散と一致するため、推定値\(\sigma^2\)は
\begin{align*}
\sigma^2 &= \frac{\scriptsize 1}{n – \scriptsize1} \sum_{i=1}^n (X_i – \bar{X})^2\\
&= \frac{\scriptsize(170 – 170)^2 + (160 – 170)^2 + (178 – 170)^2}{\scriptsize 2} \\
&= \scriptsize 84
\end{align*}
データ数が「3」なので、割る数は「2」であることに注意しましょう
不偏分散のn-1で割る理由をゆるく解説
母分散を推定するときは「不偏分散」を用い、不偏分散では割る数が「n-1」であることを学習しました。
なぜ「n-1」で割った不偏分散が推定するのに適切なの?
と疑問に思った方も多いのではいでしょうか。
ここでは「n-1」で割る理由をイメージで理解して、次の見出しで厳密に解説していきたいと思います。
発展的な内容ですが、興味がある方はぜひご覧ください。
簡単のため、母集団の分布は正規分布に従うとします。
正規分布について詳しく知りたい方は下記の記事をご覧ください。
代表的な確率分布を一通り解説しています。

母集団は図の青線の正規分布に従い、母集団から4つのデータをランダムに抽出して赤点でプロットしました。
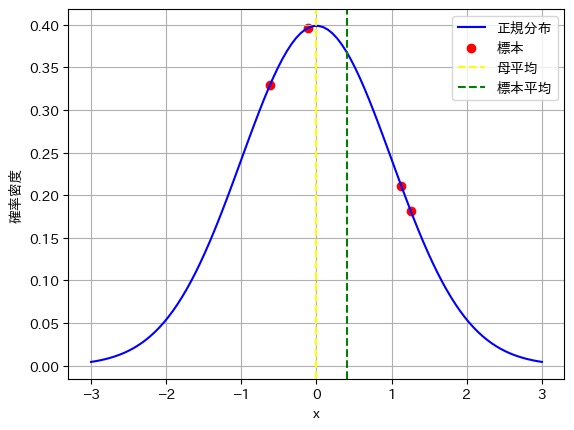
母集団は正規分布なので、母平均はグラフの中心(黄色い線)となります。
4つのプロットしたデータの標本平均は緑色の線で表しています。
分散は「平均からの散らばり具合」を意味し、母分散は「母平均からの散らばり具合」を表します。
しかし、実際のデータでは母平均を求めらるとは限らず、標本平均を使わなくてはならないことが多いです。
「標本平均から各標本データの距離」は「母平均から各標本データの距離」より小さくなってしまうため、標本平均では散らばり具合が小さく見積もれてしまいます。
この過小評価分を補正するために不偏分散では「n」ではなく「n-1」で割っています。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
推定量の評価 〜 不偏分散のn-1で割る理由を解説
不偏分散の「n-1」で割る理由をゆるく解説して、標本平均では分散が過小評価されてしまうことを学習しました。
この章では、不偏分散についてより厳密に解説していきます。
推定量の評価
推定量の良さを評価するための指標として「一致性」、「不偏性」、「有効性」があります。
一致性
一致性は、標本の大きさ𝑛が大きくなるに従い、推定量が真の母数に近づく性質を意味します。
この一致性は、「標本平均」、「標本分散」、「不偏分散」全てにおいて成立します。
一致性の証明は難しいので証明は割愛しますが、標本を限りなく多く集めると標本平均と母平均が近づくイメージは持ちやすいと思います。
また、標本分散と不偏分散の式より、nを限りなく大きくすると、この二つの値も一致することが分かります。
不偏性
不偏性は、推定量\(\hat{\theta}\) の期待値が真の母数\(\theta\)となる性質を意味します。
また、不偏性を満たす推定量を不偏推定量と言います。
期待値について詳しく知りたい方は下記の記事をご覧ください。

不偏性は、「標本平均」、「不偏分散」では成り立ちますが、「標本平均」では成り立ちません。
この不偏性が、分散の推定量として標本分散ではなく不偏分散を用いる根拠となっています。
以下では実際に期待値を計算して、確かめていきます。
標本平均の期待値
標本平均の期待値\(E[\bar{X}]\)は、母平均uを使って表すと
\begin{align*}
E[\bar{X}] &= E[\frac{\scriptsize 1}{n} \sum_{i=1}^n x_i] \\
&=\frac{\scriptsize1}{n} \sum_{i=1}^n E[x_i] \\
&= \frac{\scriptsize1}{n} \sum_{i=1}^n u \\
&= u
\end{align*}
標本平均\(\bar{X}\)は母平均𝜇の不偏推定量であることが分かります。
標本分散の期待値
標本分散の期待値\(E[S^2]\)を母平均\( \sigma^2\)を使って表すと
\begin{align*}
E[S^2] &= E[\frac{\scriptsize 1}{n} \sum_{i=1}^n (X_i – \bar{X})^2]\\
&= \frac{n-\scriptsize 1}{n} \times \sigma^2
\end{align*}
となります。(細かい計算は割愛)
したがって、標本分散は母分散\( \sigma^2\)の不偏推定量でないことが分かります。
不偏分散の期待値
不偏分散の期待値\(E[U^2]\)を母平均\(\sigma^2\)を使って表すと、
\begin{align*}
E[U^2] &= E[\frac{n}{n-\scriptsize 1} S^2]\\
&= \frac{n}{n-\scriptsize 1} \times \frac{n-\scriptsize 1}{n} \sigma^2 \\
&= {\sigma}^2
\end{align*}
標本分散は母分散\( \sigma^2\)の不偏推定量でないことが分かります。
したがって、母分散の推定値として、標本分散より不偏分散が適切であるということが不偏推定量より示せました。
有効性
「不偏性」と「一致性」を備えた2つの推定量を比較する際に用いて、最も分散の小さい不偏推定量であることを意味します。











