連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第12章では、「仮説検定」について解説します。
検定で登場する「帰無仮説」や「対立仮説」「有意水準」などの用語や検定の手順を具体例を用いながら解説しています。
初学者も理解しやすいように丁寧に解説しているので、ぜひ最後までご覧ください。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章:平均・分散などの基本統計量
2章:相関関係
3章:確率の基本
4章:条件付き確率・ベイズの定理
5章:期待値
6章:代表的な確率分布
7章:母集団と標本
8章:標本平均・不偏分散
9章:中心極限定理
10章:母平均の推定(分散既知)
11章:母平均の推定(分散未知)
12章:仮説検定
13章:正規分布を用いた検定
14章:【t検定】母平均を検定
15章:【F検定】分散に差があるか?
16章:ウェルチの検定
17章:カイ2乗検定
18章:分散分析
19章:回帰分析
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
仮説検定の基本用語
「仮説検定とは何か」そして、仮説検定で登場する基本的な用語について解説します。
仮説検定
仮説検定とは、母集団についての仮説を標本に基づいて検証することを意味します。
仮説検定は、単に「検定」と呼ぶこともあるので注意しましょう。
具体例を見て、仮説検定のイメージを掴みましょう。
仮説検定の例
あるコインAを1回投げたとき、表が出る確率を「p」とします。
コインAを10回投げたとき、9回表が出ました。
この事実から「コインAには歪みがある(p ≠ 0.5)」という仮説は立てました。
この仮説が正しいか数学的手法を用いて検証します。
感覚的には、
コインを10回投げたとき、9回表が出たらそのコインは歪んでいる
と判断するでしょう。
しかし、理論上「コインは歪んでいないが、偶然10回中9回表が出た」という可能性もあり得ます。
仮説検定では、確率論を用いて「コインAに歪みがあるか」を判断します。
実際に、この例題で仮説検定を簡単に行なってみましょう。
「コインが歪んでいない(p = 0.5)」と仮定したとき、コインが10回中9回表の出る確率\(f(\scriptsize 9)\)は
$$
f(\scriptsize 9) = {}_{10} C_9 \times ({\scriptsize 0.5})^{{\scriptsize 9}}({\scriptsize 0.5})^{{\scriptsize 1}} = {\scriptsize 0.0098}
$$
より極端な事象であるコインが10回中10回表の出る確率\(f(\scriptsize 10)\)は
$$
f(\scriptsize 10) = (\scriptsize 0.5)^{\scriptsize 10} = 0.0009
$$
と計算できます。
よって、コインを10回投げたとき、9回あるいは10回表が出る確率Pは
$$
P = f({\scriptsize 9}) + f({\scriptsize 10}) = \scriptsize 0.0107
$$
となります。
すなわち、「コインが歪んでいない(p = 0.5)」と仮定した場合、コインを10回投げたとき、9回あるいは10回表が出る確率は「約1%」です。
「1%」を起こり得る確率と判断すれば「コインは歪んでいるとは言えない」と判断します。
逆に、「1%」が非常に稀であり現実的に起こり得ないと判断すれば「コインは歪んでいる」と判断します。
この基準の設定については「有意水準」という用語の紹介で説明します。
帰無仮説
帰無仮説は、間違っていることを証明したい(棄却したい)仮説を指します。
先ほどの問題の場合、「コインが歪んでいる(p≠ 0.5)」と証明しようとしているので、帰無仮説は「コインが歪んでいない(p = 0.5)」とします。
対立仮説
対立仮説は、帰無仮説に対立する仮説であり、本来証明したい仮説です。
先ほどの問題の場合、対立仮説は「コインが歪んでいる(p≠ 0.5)」とします。
なぜ帰無仮説が必要なのか?
と疑問に思った方も多いのではないでしょうか。
これは、一般に科学的エビデンスを得る際に「〇〇ではない」という仮説を棄却することで理論を構築することが由来しています。
例えば、「水は100度で沸騰する」という仮説を立てたとします。
平地のどんな場所でも、水が100度で沸騰するという実験結果が得られるでしょう。
しかし、富士山(標高が高い場所)で実験を行うと、「88度で沸騰する」という実験結果が得られます。
この実験結果から「水は100度で沸騰する」という仮説は棄却され、新たに「気圧によって水の沸点が変化する」といった仮説を立てるでしょう。
このように、科学的エビデンスは実験結果に応じて当初の仮説を棄却し、新たな仮説を立ててそれを証明しようとすることで構築されていきます。
仮説を支持するためのデータはいくらあってもキリがないですが、仮説を棄却するデータは一つで十分です。
これを踏まえて、仮説検定では「帰無仮説(証明したい仮説でない)を棄却する」というダブルネガティブな手法を取ります。
参考:https://www.amed.go.jp/content/000034155.pdf
p値
p値とは、母集団において帰無仮説が正しいと仮定した場合に、標本データで観測された事象とそれ以上に仮説から外れた事象が起こる確率の実現値を表します。
p値は、確率を表す英単語「Probability」に由来しています。
「仮説検定の例」でp値について確認してみましょう。
標本データは、「コインAを10回投げたとき、9回表が出た」という結果が得られました。
しかし、コインが歪んでいない(p = 0.5)のであれば、表が出る回数は10回中5回程度になるはずです。
したがって、実際に観測された「10回中9回表が出る事象」と仮説からさらに外れた「10回中10回表が出る事象」が起こる確率Pをp値として計算しました。
有意水準
有意水準とは、 帰無仮説を棄却する基準となる確率を表します。
言い換えると、標本データから得られるp値が「ある確率」以下の時、確率的にあり得ない状態とみなし、「ある確率」が有意水準にあたります。
有意水準は「α」で表されることが多く、1%, 5%, 10%が主流となっています。
有意水準「α = 0.05」と設定した場合は、p値が0.05を下回った時、確率的にあり得ない状態とみなし、帰無仮説を棄却します。
逆に、p値が0.05を上回った時、確率的に起こり得る事象だと考え、帰無仮説を受容します。
有意水準は多くの場合「α = 0.05」と設定しますが、データが十分に集まったり、間違いが許されなかったりする場面ではより小さい値を設定します。
有意水準は検定を行う前に事前に設定しなければなりません
第一種の誤りと第二種の誤り
仮説検定は標本データから確率的に採択・棄却が決まるため、誤った結論を導く可能性があります
この「誤り」の種類が2種類あるため確認しておきましょう。
第一種の誤り
1パターン目の誤りは、「第一種の誤り」です。
「第二種の過誤」と呼ばれることもあります。
第一種の誤りは、帰無仮説が正しいが、正しくないと判断(棄却)されてしまうケースです。
「例」:容疑者Aは犯人ではないが、有罪と判定
第二種の誤り
2パターン目の誤りは、「第二種の誤り」です。
「第二種の過誤」と呼ばれることもあります。
第二種の誤りは、帰無仮説が正しくないが、正しいと判断(採択)されてしまうケースです。
「例」:容疑者Aは犯人だが、無罪と判定
仮説検定の手順
仮説検定の詳細な手順を説明します。
仮説検定の手順
- 帰無仮説\(H_0\)、対立仮説\(H_1\)を設定する
- 帰無仮説\(H_0\)を真として、統計量の分布を求める
- 有意水準を決める
- 有意水準と統計量の分布から、棄却域を設定する
- 標本から得られた結果が確率的に起こり得るなら、帰無仮説\(H_0\)を受容・対立仮説\(H_1\)を棄却
- 標本から得られた結果が確率的に起こり得ないなら、帰無仮説\(H_0\)を棄却・対立仮説\(H_1\)を採択
「帰無仮説を真とする」気持ちは
帰無仮説は間違っていると思うけど、その仮説を一旦認めて計算してみるね
→(帰無仮説を棄却し)、やっぱり対立仮説が正しかったね
という展開を狙っています。
次の章で「正規分布を用いた検定」を実際に行います。
練習問題を解いて、仮説検定をさらに理解しましょう。

両側検定/片側検定
仮説検定には、「両側検定」と「片側検定」の2種類の検定があります。
両側検定と片側検定の違いについて理解しましょう。
両側検定
両側検定は、得られた値が目標値と等しいかどうかを調べる際に利用します。
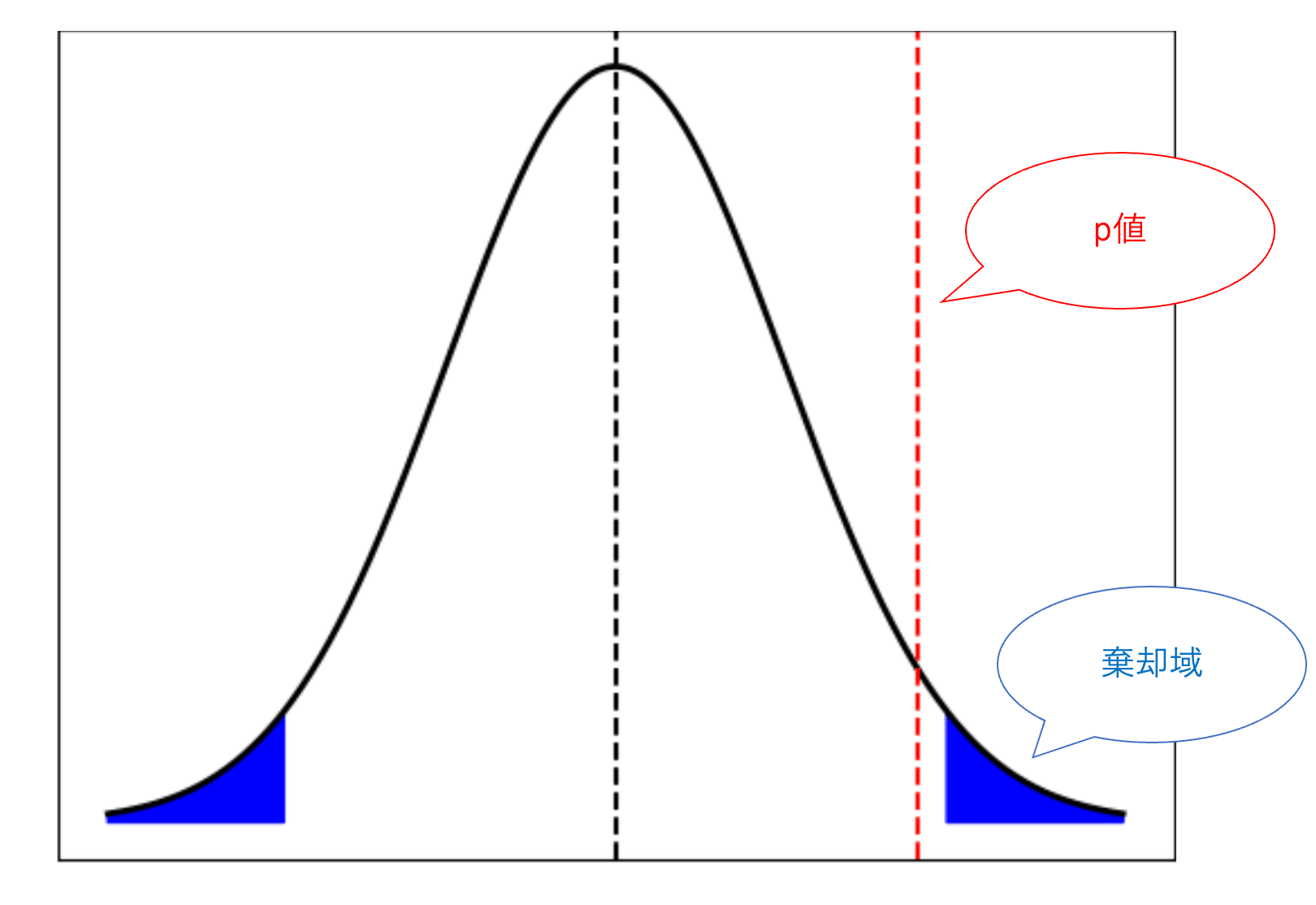
「仮説検定の例」では、「コインAには歪みがある(p ≠ 0.5)」か「コインAには歪みがないか(p = 0.5)」を検定しました。
したがって、表の出る確率が目標値0.5と一致しているかを調査しているため、両側検定を行なっていたことが分かります。

片側検定
片側検定は、得られた値が比較値よりも大きい(小さい)かどうかを調べる際に利用します。
「仮説検定の例」で片側検定について考えてみましょう。
「仮説検定の例」では、コインAを10回投げたとき、9回表が出ました。
この標本データから「コインAは表が出やすくなっている」と考え、対立仮説を「p > 0.5」と設定した場合は片側検定をすることになります。
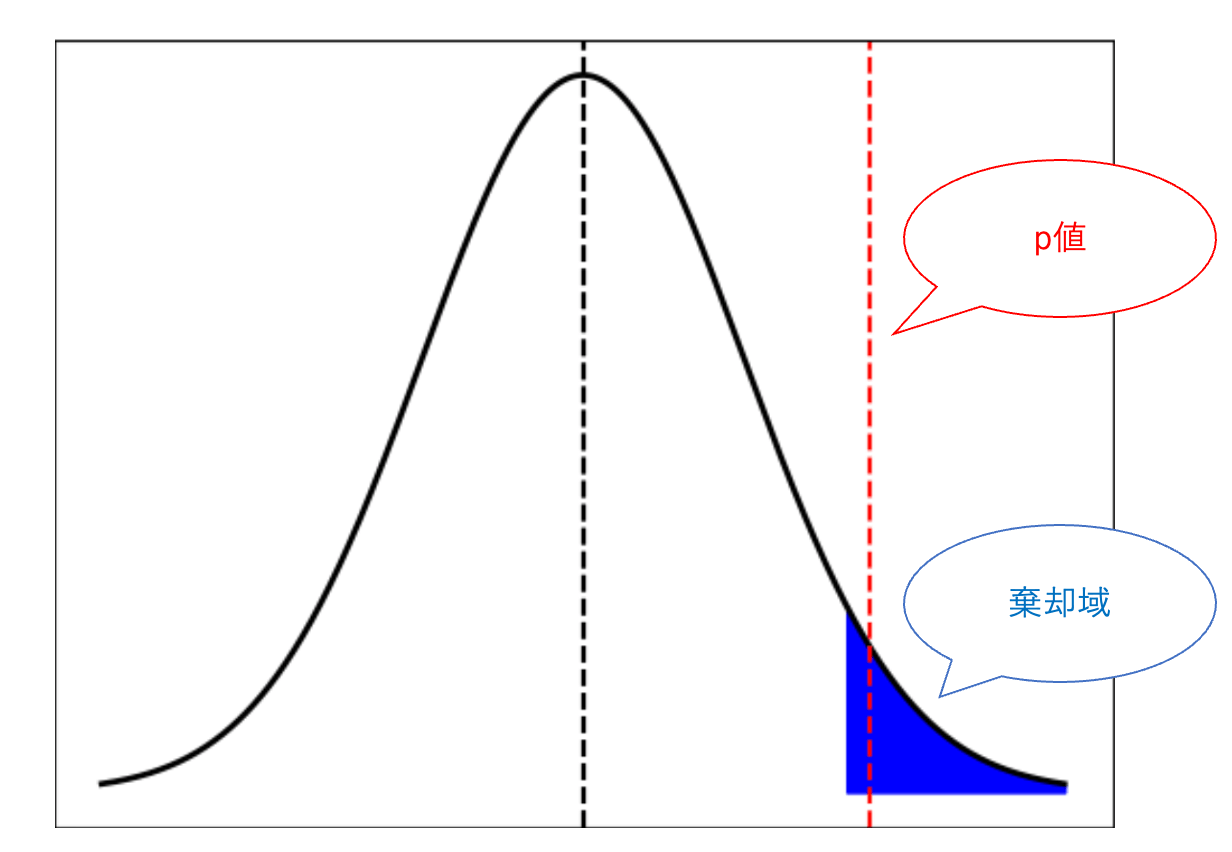
「両側検定」と「片側検定」のどちらの検定を用いるかによって、同一の有意水準を使った場合でも棄却域が異なるため、結果が異なり場合があります。
次章以降では、正規分布やt分布を用いた検定を解説していきます。










