第9章では、仮説検定として、z検定とt検定について解説していきます!
これらは、母平均と母比率の推定・仮説検定に用いる手法です。
前章の復習にもなるので、その気持ちで頑張っていきましょう!
また、本章で用いるExcelファイルは以下からダウンロードして下さい!
本連載講座【Excelによる統計解析講座】では、Excel未経験の方、自身の無い方でも順を追って学習でき、基礎からデータ分析に必要なスキルまでを身に付ける事が出来ます。
画像が多く、ビジュアルで理解しやすくなっておりますので、読み物が得意ではないという方も大丈夫です!
また、第7章からは、統計学の分野も扱う為、様々な方に役立つ講座となっております。
そのため、
- Excelを仕事で使う可能性のある方
- Excelに自信のない方
- データ分析をExcelでやりたい方
等は是非、TechTeacherが運営する【Excelによる統計解析講座】を使って学習していって下さい!
〈目次〉
第1章:【テーブル】Excelのテーブル(フィルター)を解説!
第2章:【SUM,AVERAGE】Excelの基本的な関数を解説!
第3章:【XLOOKUP,COUNTIF】データ分析の為のExcel関数を解説!
第4章:【棒,折れ線,散布図】Excelの基本的なグラフを解説!
第5章:【ピボットテーブル】Excelの便利機能”ピボットテーブル”を紹介!
第6章:【プレゼン資料】Excelグラフの体裁の整え方について解説!
第7章:【相関分析】相関係数と共分散をExcelを用いて解説!
第8章:【確率変数・正規分布】確率変数や正規分布をExcelで解説!
第9章:【t検定・z検定】母平均と母分散の仮説検定について解説!
第10章:【t検定・z検定】2つの集団の母平均・母比率の仮説検定を解説!
第11章:【仮説検定】カイ二乗検定とF検定をExcelで一瞬で解く!
t分布とは
これから行うz検定とt検定の違いは、検定に使用する分布曲線の違いです。
z検定では標準正規分布を、t検定では、t分布を使います。
標準正規分布については、前章の【確率変数・正規分布】確率変数や正規分布をExcelで解説!で学習したので、今回はt分布について説明します。
t分布とは
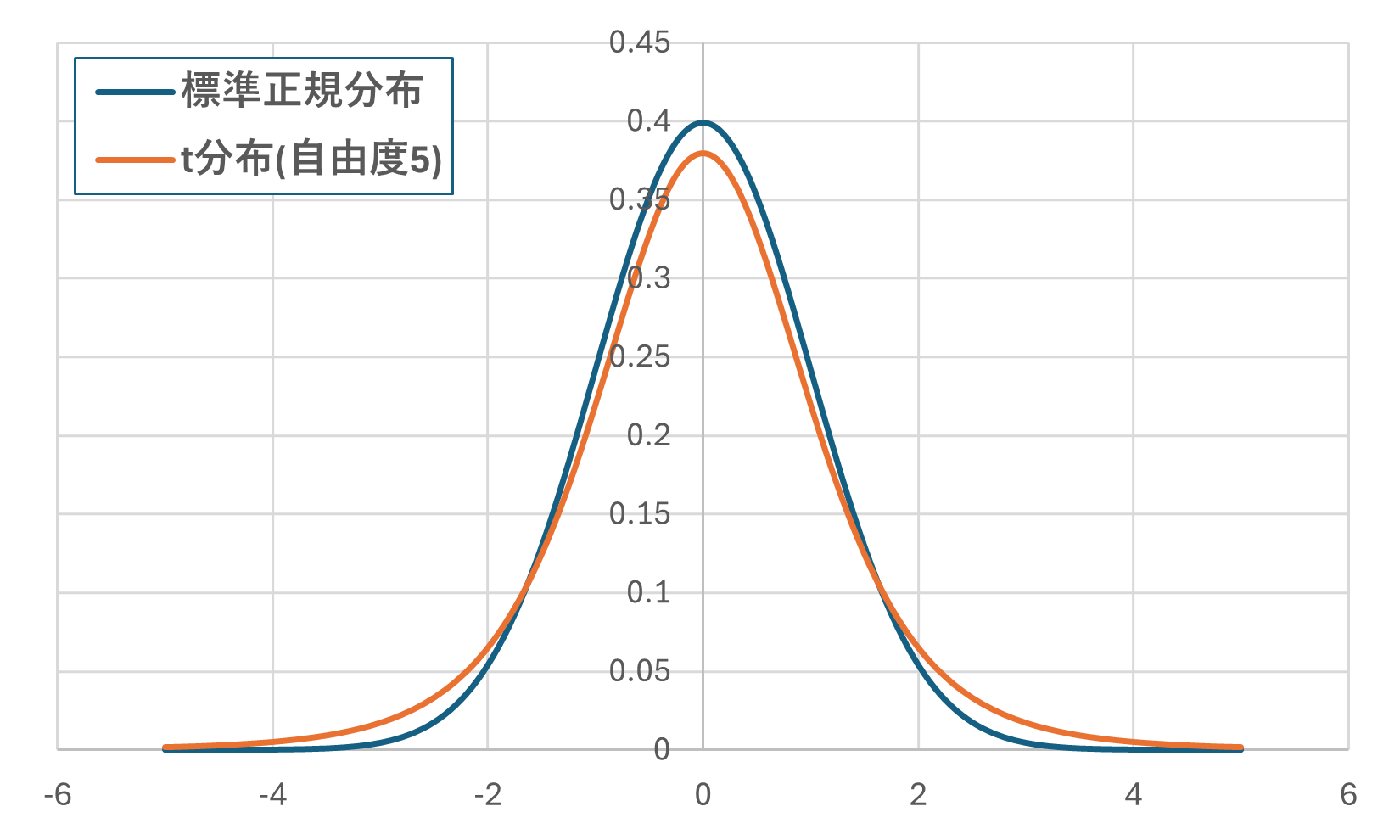
t分布は、自由度といった、いくつの変数が自由に決められるかの値で決まり、自由度が大きい程、t分布は標準正規分布に近づきます。
※自由度に関しては、母平均の推定の例題等を行っていくうちに分かってきますので、現時点では分からなくても大丈夫です!
実際に、t分布は以下の様になりますが、ここでは、「自由度が小さい程、標準正規分布より緩やかになる分布曲線がt分布」と覚えていただければ大丈夫です!
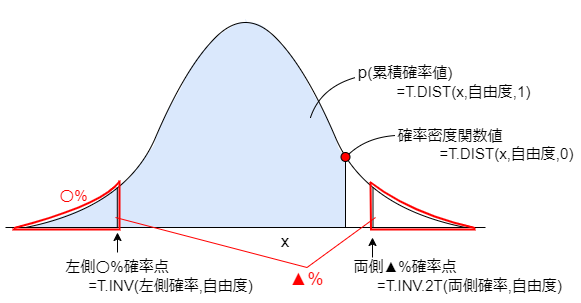
Excel関数によるt分布の値の算出方法
t分布に関するExcel関数は次の様になっています。
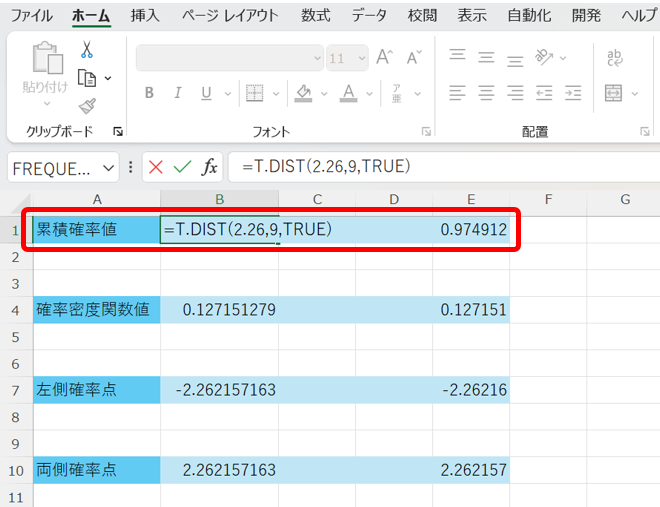
まず、任意データxに対する累積確率値は、以下の関数で算出できます。
=T.DIST(x,自由度,TRUE)
なお、TRUEの部分は1でも大丈夫です。
これを行うと、以下の様になります。
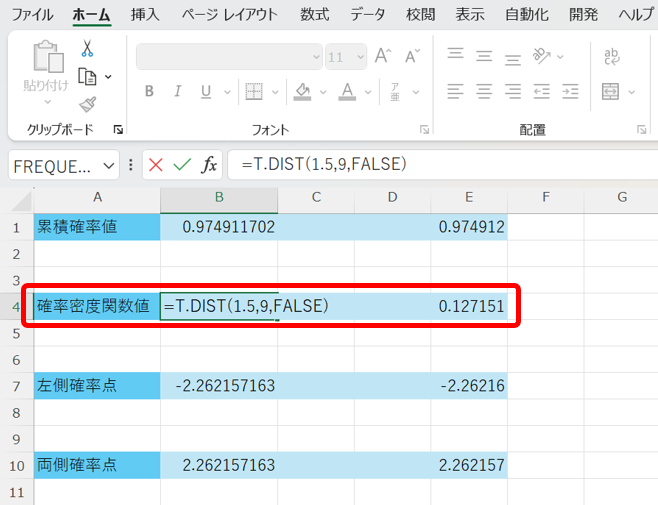
次に、確率密度関数値とは、前章の応用問題2で少し触れましたが、任意データxの時の分布曲線の縦軸の値です。
任意データxに対する確率密度関数値は、以下の関数で算出できます。
=T.DIST(x,自由度,FALSE)
なお、FALSEの部分は0でも大丈夫です。
これを行うと、以下の様になります。
続いて、左側確率点とは、左側から数えて、累積確率が〇%になる時のxの値です。
任意の確率に対する左側確率点は、以下の関数で算出できます。
=T.INV(左側確率,自由度)
これを行うと、以下の様になります。
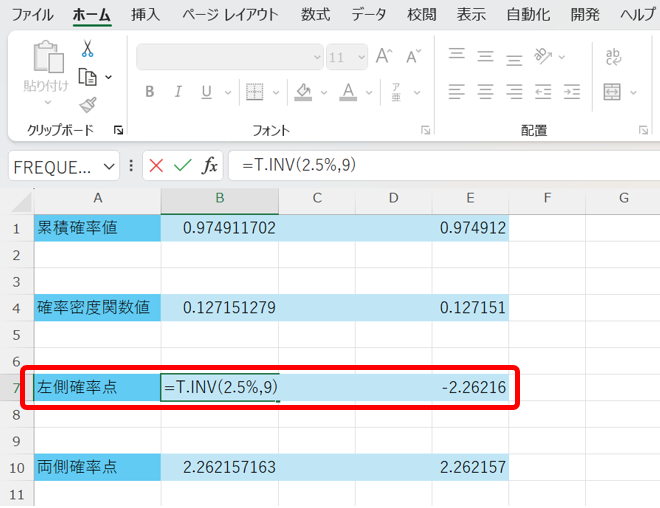
t分布も、標準正規分布と同様に、左右対称なので、〇%左側確率点の値のマイナスを取ると、〇%右側確率点になります。
最後に、両側確率点とは、両端から数えた累積確率の合計が▲%になる時のxの値の絶対値です。
任意の確率に対する両側確率点は、以下の関数で算出できます。
=T.INV.2T(両側確率,自由度)
これを行うと、以下の様になります。
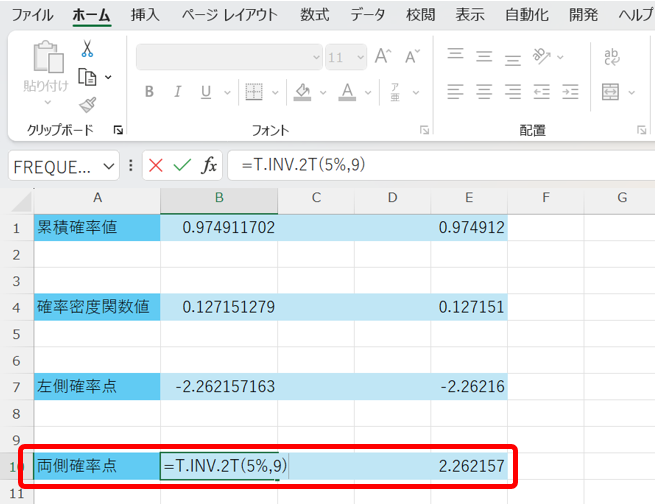
この結果からも分かりますが、両側確率点では、両側の累積確率を等しくしている為、▲%両側確率点と\(\frac{\text{▲}}{2}\) %左側確率点の絶対値は同じになります。
つまり、5%両側確率点は2.5%左側確率点と等しくなります。
仮説検定とは
帰無仮説と対立仮説
仮説検定とは、ある仮説に対して、それが正しいかどうかを検定する事です。
仮説検定の際には、棄却したい仮説(=帰無仮説)と採択したい仮説(=対立仮説)を立てます。
例えば、
仮説検定の例
C会社が、販売している空気清浄機Hの効果を検定したい。
100個の加湿器Hの使用前と後について、部屋の中の湿度を検証し、その結果から加湿器Hの効果があるかどうかについて検定する。
この時、
帰無仮説:「湿度は変化しなかった(湿度の上昇幅の母平均µはµ=0)」
対立仮説:「湿度は変化した(µ≠0)」or「湿度は上がった(µ>0)」
などとします。
この時、帰無仮説を棄却する事で、対立仮説を採択する事が出来ます。
両側検定と片側検定
では、どのようにして検定を行っていくのかといった点に関して、両側検定と片側検定といった方法が存在します。
対立仮説が「湿度は変化した(µ≠0)」である時、標本平均から予測された母平均が十分離れていれば帰無仮説を棄却する事が出来ます。
この時、両側検定を用いる事で、母平均が標本平均を上回っても、下回っても棄却する範囲(=棄却域)を設ける事が出来ます。
これに対し、対立仮説が「湿度は上がった(µ>0)」である時、母平均の検定量が標本平均の検定量を上回る可能性のみを棄却したいので、片側検定(この場合は右側検定)を行います。
なお検定量とは、仮説検定を行う際に、用いる統計量です。
これらの内容をまとめると、以下の様になります。
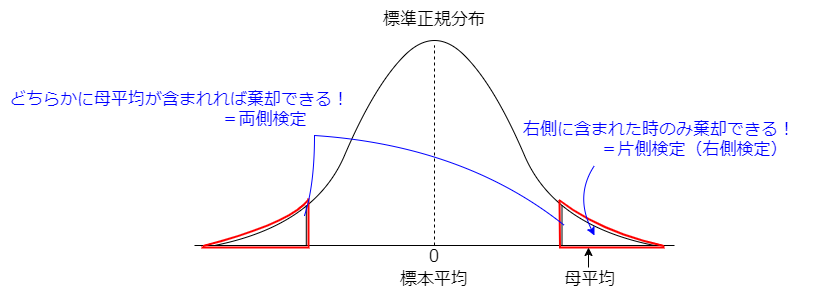
片側検定で棄却域にするのは左側じゃないの?と思った鋭い方々へ
片側検定の説明において、「母平均の検定量が標本平均の検定量を上回る可能性のみを棄却したい時に右側検定をする」とありました。
私がこの分野を始めて学習した時、「母平均が大きいことを証明したいのだから、上側を棄却しちゃだめじゃないか」と思いました。
これについて、詳しく説明していきたいと思います。
まず、母平均の「検定量」が右側検定で棄却された場合について考えてみましょう。
この時、母平均の「検定量」は、標準正規分布において、より左側にあると考えられます。
ここで、前章の標準化の方法について思い出してみましょう。
「正規分布の個々のデータから平均値を引き、標準偏差で割る」事によって、基準化が出来、これを計算式で表すと、検定量Zは以下の様になります。
\[Z=\frac{\text{標本平均}-\text{母平均}}{\text{標準偏差}}\]
これを踏まえて、母平均の検定量Zについて、右側検定を行って棄却出来た場合、検定量Zはより小さくある必要があります。
つまり、母平均がより大きい値である必要がある訳です。
その為、対立仮説に母平均が大きい事を設定した場合、右側検定をする必要があります。
標準誤差
統計に用いられる、データの基本的な特性を表すものを、基本統計量と言います。
標準誤差とは、平均値と標準偏差に並んで、基本統計量に含まれる統計量で、仮説検定に用います。
この標準偏差はSEで表され、以下の式で計算できます。
\[ \text{SE} = \frac{\text{σ}}{\sqrt{n}} \]
この式から、SEはデータがばらついている(=標準偏差が大きい)程大きくなり、データ数が大きい程小さくなります。
仮説検定の手順
では、以下に仮説検定をどのようにして行っていくのかについて説明したいと思います。
- 帰無仮説と対立仮説を立てる。
- 基本統計量(平均値、標準偏差、標準誤差)を算出する。
- 検定統計量(p値、T値、信頼区間)を算出する。
- 有意差判定を行う。
有意差判定とは、帰無仮説が棄却できるかを判断するといった事であり、その方法は用いる検定統計量によって違います。
また、その検定統計量について、仮説検定では、p値、T値、信頼区間を用いた、3つの方法があります。
しかし、全て導き出される結果は同じになります。
そのため本講座では、最も簡単なT値を用いた検定に絞って説明します。
T値による仮説検定
T値とは、比較する平均値の差分を標準誤差で割った値で、以下の式で計算できます。
\[ \text{T値}=\frac{\text{標本平均}-\text{比較値}}{\text{SE}} \]
今回の場合、標本平均は湿度の変化量の平均、比較値は帰無仮説より0になります。
またこのT値は、データ数に依存して、標準正規分布もしくはt分布に従う事が分かっています。
更に、T値を用いて帰無仮説を棄却する際の基準となる指標を棄却限界値と言います。
この棄却限界値は、信頼度によって決まります。
更に、100%から信頼度を引いた値を有意水準と言います。
例えば、信頼度95%の時の有意水準は5%であり、有意水準5%の棄却限界値よりもT値が大きくなった時、帰無仮説を棄却できます。
以下の図で、これらの言葉について、イメージで理解しておきましょう。
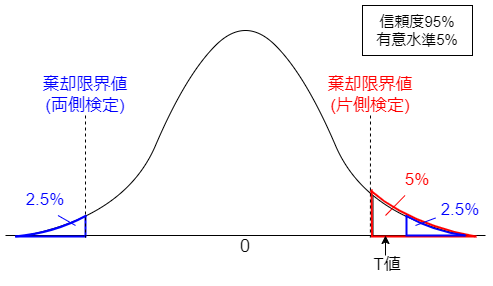
なお、この図において、共に有意水準は5%であるものの、
両側検定の時の棄却限界値<T値<片側検定の時の棄却限界値
となっているため、両側検定では帰無仮説を棄却できないものの、片側検定では棄却できる、という事になります。
仮説検定において、
- 「有意水準〇%ではだめだったけれど、△%であれば棄却できるから、△%でなら棄却出来るとしよう」
- 「両側検定では棄却できなかったものの、片側検定では棄却できたから片側検定で棄却できるとしよう」
など、最初に決めた検定方法から、結果の都合で検定方法を変更することはタブーです。
母平均の仮説検定
長い基本の説明お疲れ様でした!
遂に、母平均の仮説検定について学んでいきましょう。
ここでは、母平均の検定の中でも、「1つの母平均と比較値が異なるか」に関する検定について説明します。
母平均の検定方法の決定
母平均の検定にはz検定とt検定の2パターンがあります。
z検定とt検定どちらで行うかの選択は、以下の様に分類できます。
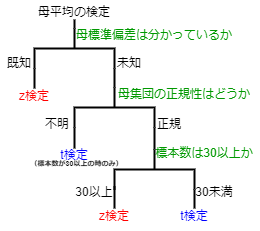
これについて、t検定では原則、データが正規分布に従わない時は使えないといったルールがあります。
しかし、中心極限定理という、所謂、「データ数が多ければ正規分布とみなしていいよ!」といった定理により、正規性が不明でも、標本数が30以上であればt検定を行う事が出来ます。
※データ数の基準は個人的な経験則によるものであり、20個程度で大丈夫と言う人もいます。
母平均の仮説検定
では、ついに、母平均の仮説検定を行ってみましょう!
例題1(母平均の仮説検定)
C会社が、販売している空気清浄機Hの効果を検定するために、100個の加湿器Hの使用前と使用後について、部屋の中の湿度を測定した時、この結果から加湿器Hの効果があるかどうかについて、有意水準5%で検定してみましょう。
ただしここでは、湿度が3%以上湿度が上がる事をもって、加湿器の効果があるとみなします。
なお、母集団の標準偏差及び母集団正規性は不明とします。
※結果については、Excelファイルの2ページ目をご参照下さい。
では、仮説検定の手順に従って検定を行っていきましょう!
まず、①帰無仮説と対立仮説を立てます。
加湿器Hの使用前と使用後の変化の差をµとすると、今回の帰無仮説と対立仮説は次の様になります。
帰無仮説:µ=3
対立仮説:µ>3
これより、今回は片側検定(右側検定)を行います。
次に、②基本統計量(平均、標準偏差、標準偏差)を算出します。
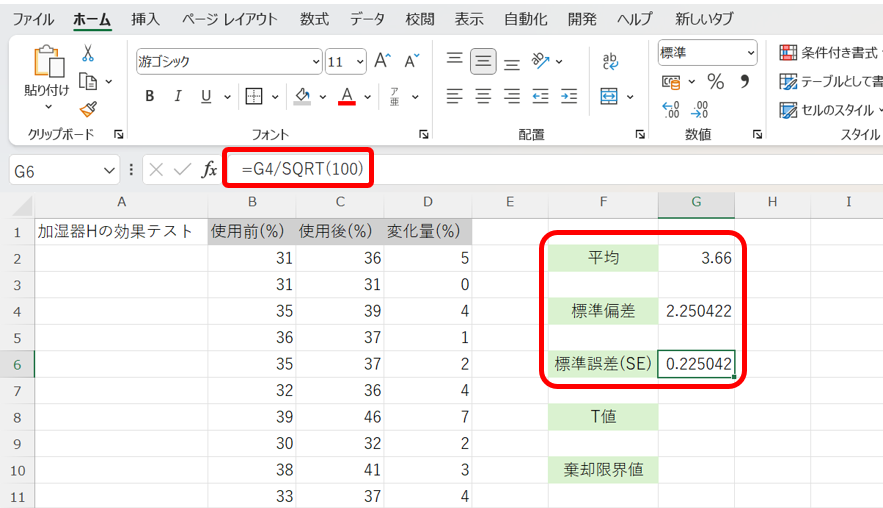
これより、平均は3.66、標準偏差は約2.25、SEは約0.23であることが分かります。
次に、③検定統計量を算出します。
今回、母標準偏差と母集団正規性は分かっておらず、データ数は100(>30)であることから、t検定を行います。
この時、基本統計量から、T値は以下の様にして算出できます。
\[ \text{T値}=\frac{\text{標本平均}-3}{\text{SE}} \]
また、有意水準5%でt分布に関して右側検定を行うので、棄却限界値は以下の関数により計算されます。
=T.INV(0.95,99)
これに関して、T.INVは左からの累積確率が95%になる時の基準値を返すので、右側から5%の時の値と同じになります。
また、自由値に関して、今回のデータは100個であり、標本平均が計算に用いられている為、自由に決定できるデータ数は99個になります。
このように、データ数nの時、母平均のt検定の自由度はn-1になります。
これらをExcel上で計算すると、以下の様になります。
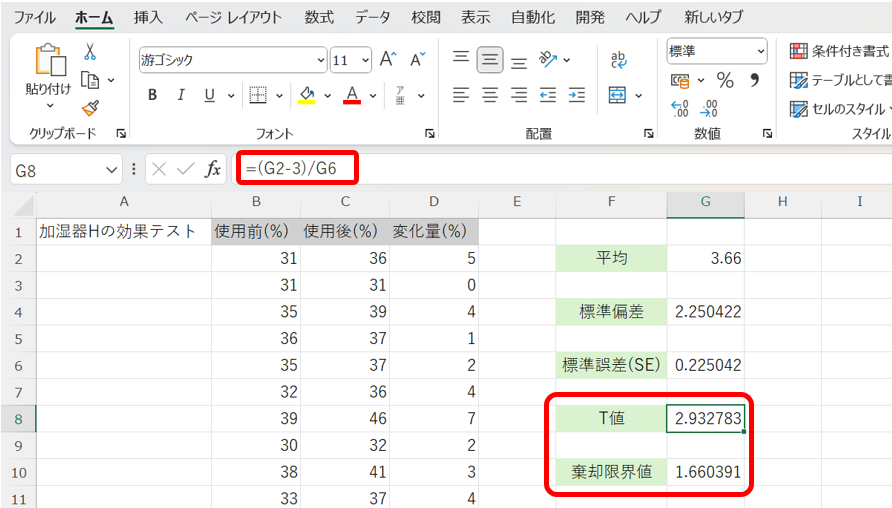
これより、T値は約2.93、棄却限界値は約1.66である事が分かります。
最後に、④有意差判定を行います。
この結果から、棄却限界値<T値であるから、この帰無仮説は有意水準5%で棄却する事が出来ます。
つまり、µ>3で、加湿器Hは効果があるという事が出来ます。
製品の検定など、基本的な仮説検定には、主に有意水準5%(信頼度95%)が用いられます。
ただし、医療関係など、人命がかかわる検定に関しては、主に有意水準1%(信頼度99%)が用いられます
母比率の仮説検定
最後に、母比率の仮説検定を行っていきます。
例題2(母比率の仮説検定)
C社の加湿器Hについて、テレビのCMで宣伝を行いました。この宣伝の効果を確かめるために、T市でランダムに選んだ100人に対して認知度調査を行った所、加湿器Hを知っている人は60人で、認知率は60%でした。
この時、CMによって、T市全体における加湿器Hの知名度が50%を超えたかを有意水準5%で仮説検定してみましょう。
母比率の仮説検定で使えるのは、z検定のみです。
簡単な計算になっているので、今回はExcelを使わずにやってみましょう!
母平均の時と同様に、まずは①帰無仮説と対立仮説を立てます。
この時、T市全体における加湿器Hの認知度をxとすると、以下の様になります。
帰無仮説:x=50%
対立仮説:x>50%
これより、今回も片側検定(右側検定)を行っていきます。
次に、②基本統計量に関して、母比率の検定では、平均や標準偏差が無いので、標準誤差(SE)のみ求めていきます。
母比率の検定における標準誤差は以下の式で計算されます。
\[ SE=\frac{\sqrt{\text{比較値}\times(1-\text{比較値})}}{\sqrt{n}}\]
その為、今回は以下の様に計算できます。
\[ SE= \frac{\sqrt{0.5\times(1-0.5)}}{\sqrt{100}}=0.05 \]
続いて、③検定統計量(T値)を算出します。
標本比率=0.6、比較値=0.5、SE=0.05なので、T値は以下の様に計算できます。
\[ \text{T値}= \frac{0.6-0.5}{0.05}=2 \]
更に、z検定において、有意水準5%の片側検定における棄却限界値は1.64になります。
最後に、④有意差判定を行います。
この結果から、T値>棄却限界値である為、この帰無仮説は有意水準5%で棄却され、T市における加湿器Hの認知率は50%を超えたと判断できます。
標準正規分布における有意水準5%の右側検定の棄却限界値は、以下の関数から、約1.64と計算する事が出来ます。
=NORM.S.INV(0.95)
これについて、t分布は自由度によって変わってしまうものの、標準正規分布では有意水準のみに依存して決まります。
そのため、余裕がある方は、下の4つの値は覚えておくと良いと思います!
| 両側検定 | 片側検定 | |
| 有意水準5% | 1.96 | 1.64 |
| 有意水準1% | 2.58 | 2.33 |
※覚えなくても自然に覚えていくの大丈夫です!
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
まとめ
今回のExcelによる統計解析講座第9章では、z検定やt検定を用いた、母平均と母比率の仮説検定について解説してきました。
これらは、仮説検定の中でも最も有名な検定で、特に、t検定は汎用性が高いので、是非覚えていってください!
次章では、t検定による、2つの母集団に対する母平均の差の検定について解説していきます。
仮説検定の大まかな流れ自体は変わらないので、復習も含めて読んでみて下さい!









