第11章では、仮説検定の、カイ( \chi^{2})二乗検定とF検定について解説していきます!
カイ二乗検定はABテストなどに、F検定は母分散の比の検定に用いる事が出来ます。
前章と流れは似ているので、頑張っていきましょう!
また、本章で用いるExcelファイルは以下からダウンロードして下さい!
本連載講座【Excelによる統計解析講座】では、Excel未経験の方、自身の無い方でも順を追って学習でき、基礎からデータ分析に必要なスキルまでを身に付ける事が出来ます。
画像が多く、ビジュアルで理解しやすくなっておりますので、読み物が得意ではないという方も大丈夫です!
また、第7章からは、統計学の分野も扱う為、様々な方に役立つ講座となっております。
そのため、
- Excelを仕事で使う可能性のある方
- Excelに自信のない方
- データ分析をExcelでやりたい方
等は是非、TechTeacherが運営する【Excelによる統計解析講座】を使って学習していって下さい!
〈目次〉
第1章:【テーブル】Excelのテーブル(フィルター)を解説!
第2章:【SUM,AVERAGE】Excelの基本的な関数を解説!
第3章:【XLOOKUP,COUNTIF】データ分析の為のExcel関数を解説!
第4章:【棒,折れ線,散布図】Excelの基本的なグラフを解説!
第5章:【ピボットテーブル】Excelの便利機能”ピボットテーブル”を紹介!
第6章:【プレゼン資料】Excelグラフの体裁の整え方について解説!
第7章:【相関分析】相関係数と共分散をExcelを用いて解説!
第8章:【確率変数・正規分布】確率変数や正規分布をExcelで解説!
第9章:【t検定・z検定】母平均と母分散の仮説検定について解説!
第10章:【t検定・z検定】2つの集団の母平均・母比率の仮説検定を解説!
第11章:【仮説検定】カイ二乗検定とF検定をExcelで一瞬で解く!
カイ二乗分布
カイ二乗分布とは
Z_{1},\cdots,Z_{n} を、互いに独立で標準正規分布に従う確率変数とします。
この時、 Z_{1},\cdots,Z_{n} の二乗和、つまり、 Z^{2}_{1},\cdots,Z^{2}_{n} の従う確率分布を自由度nのカイ二乗分布( \chi^{2} 分布)といいます。
この定義が分からなくても、「ABテストなどの際にはカイ二乗分布( \chi^{2} 分布)を使う」と覚えていただければOKです!
前述した様に、カイ二乗分布( \chi^{2} 分布)はABテスト(本当に有意な差であるかの検定)に用いる事が出来ます。
これは、非常に使い勝手の良い検定です。
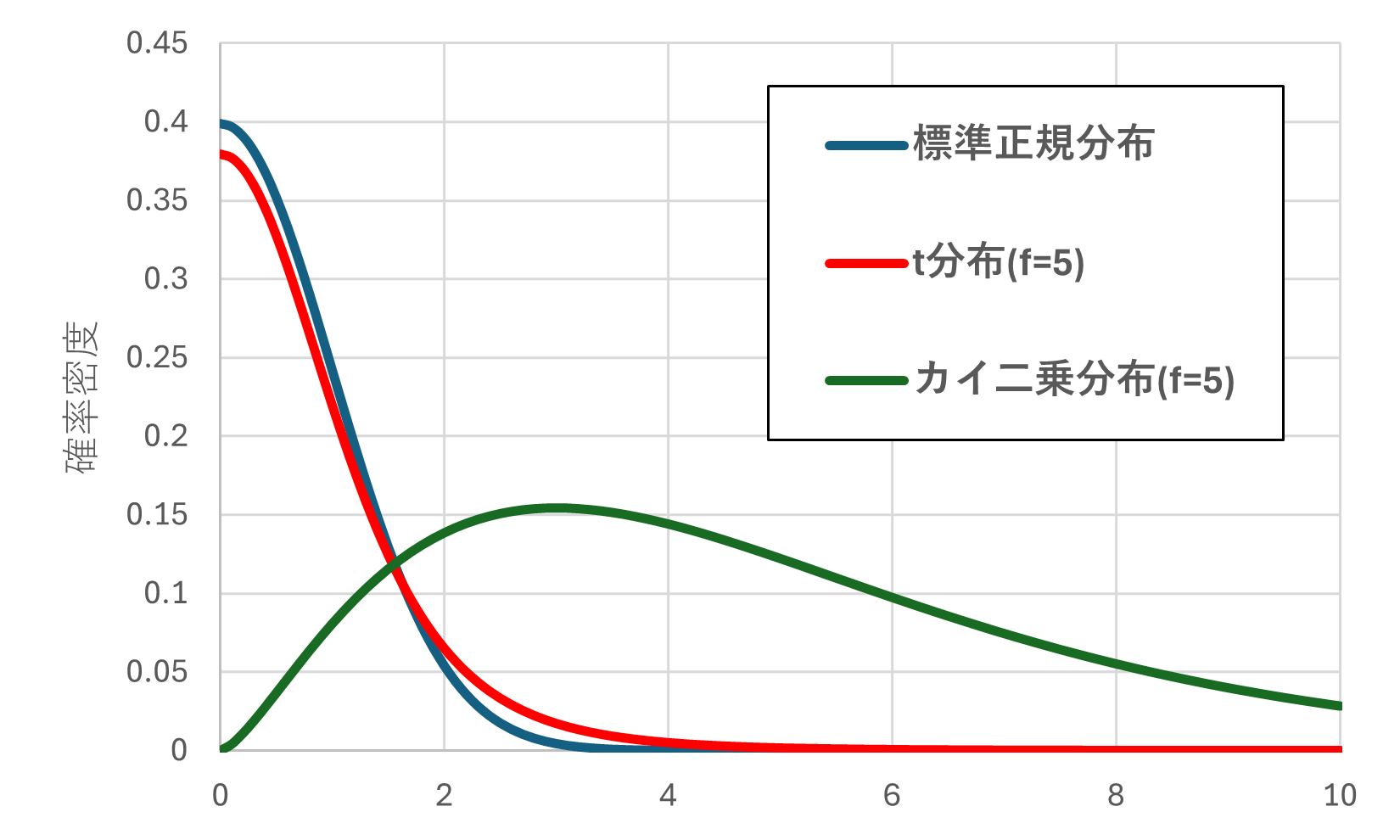
カイ二乗分布( \chi^{2} 分布)の概形は以下の様になります。
ただし、fは自由度です。
カイ二乗分布のExcel関数
では、カイ二乗検定に用いるための、Excel関数について解説していきます。
まず、カイ二乗分布の確率密度関数値は以下の関数で計算できます。
=CHISQ.DIST(x,自由度,FALSE)
次に、カイ二乗分布の左側確率点は以下の関数で計算できます。
=CHISQ.INV(左側確率,自由度)
続いて、カイ二乗分布の右側確率点は以下の関数で計算できます。
=CHISQ.INV.RT(右側確率,自由度)
これらの指す内容が分からない方は、第9章の【t検定・z検定】母平均と母分散の仮説検定について解説!内の「Excel関数によるt分布の値の算出方法」をご覧ください!
ここで、今回はカイ二乗検定の方法のみを解説していくため、実際に使うのは以下の関数だけです。
=CHISQ.TEST(実測値範囲,期待値範囲)
この関数では、カイ二乗検定を行った際のp値を求める事が出来て、このp値が有意水準を超えたら、有意差はないと判断できます。
このCHISQ.TESTに関しては、この後の例題で詳しく解説します。
F分布
F分布とは
X_{1},\cdots, X_{n} 、 Y_{1},\cdots, Y_{n} を互いに独立で、各々が自由度m、nのカイ二乗分布( \chi^{2} 分布)に従う確率変数とします。
この時、
\frac{\frac{X}{m}}{\frac{Y}{n}}
の従う確率分布を自由度(m,n)のF分布と言います。
カイ二乗分布と同様に、「母分散の比の検定にはF分布を使う」と覚えていただければOKです!
この母分散の比の検定は、2つの母分散が等しいかどうかの検定です。
つまり、対応のない母平均の検定における、母標準偏差[母分散]が等しいかの判断に用いる事が出来ます。
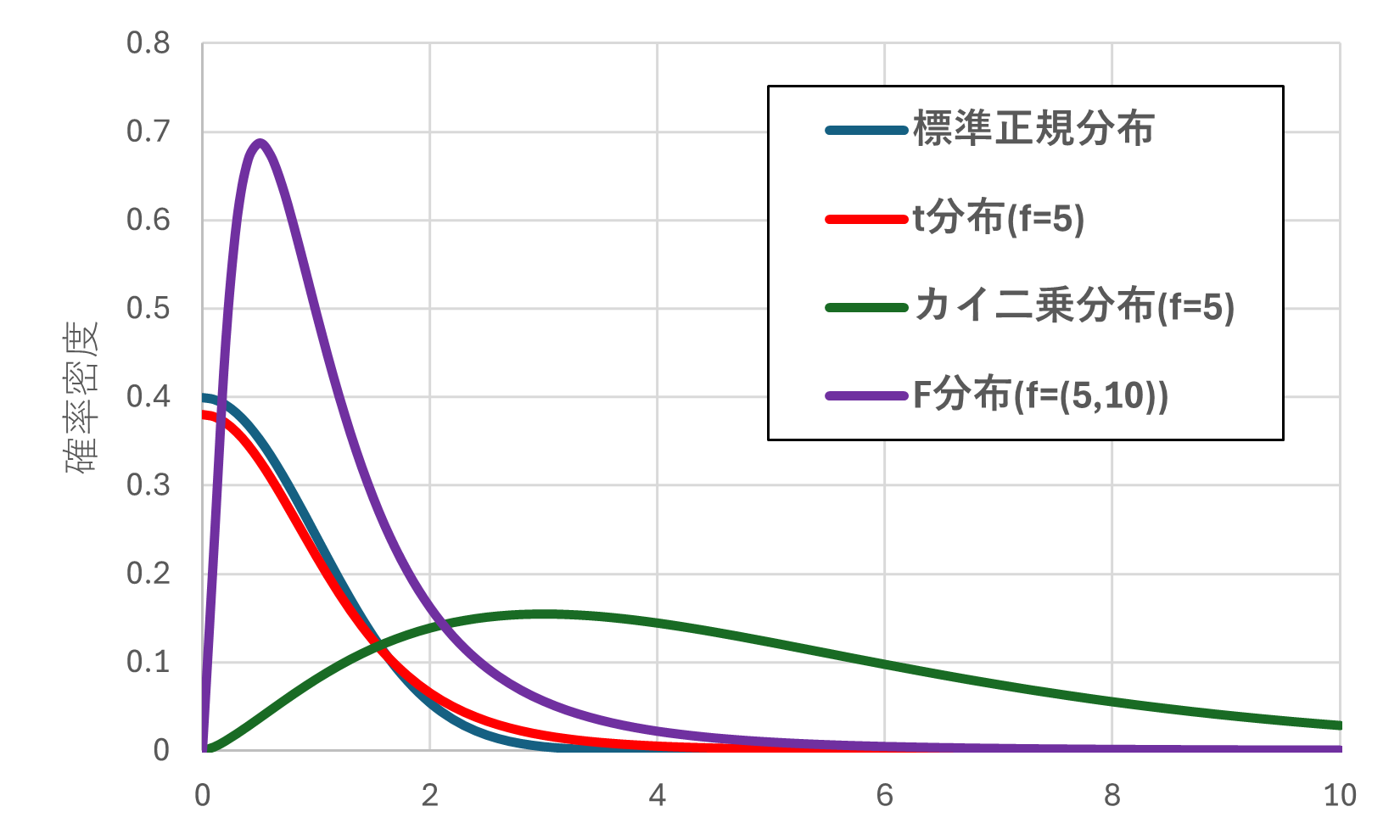
F分布の概形は以下の様になります。
F検定のExcel関数
では、F検定に用いるための、Excel関数について解説していきます。
まず、F分布の確率密度関数値は以下の関数で計算できます。
=F.DIST(x,自由度1,自由度2,FALSE)
次に、F分布の左側確率点は以下の関数で計算できます。
=F.INV(左側確率,自由度1,自由度2)
続いて、F分布の右側確率点は以下の関数で計算できます。
=F.INV.RT(右側確率,自由度1,自由度2)
これらの指す内容が分からない方は、第9章の【t検定・z検定】母平均と母分散の仮説検定について解説!内の「Excel関数によるt分布の値の算出方法」をご覧ください!
ここで、カイ二乗検定と同様に、今回はFの方法のみを解説していくため、実際に使うのは以下の関数だけです。
=F.TEST(配列1,配列2)
この関数では、F検定を行った際のp値を求める事が出来て、このp値が有意水準を超えたら、母分散は等しい(=等分散である)と判断できます。
このF.TESTに関しては、この後の例題で詳しく解説します。
カイ二乗検定
では、早速、カイ二乗検定をやっていきましょう!
例題1(カイ二乗検定)
R社では、デジタル広告の文章に絵文字を付けるかどうかについて、検討されています。そこで、絵文字ありの広告と絵文字なしの広告をランダムに表示して、それぞれのクリック率を調べる事にしました。その結果は、Excelファイル1ページ目の様になりました。クリック割合から、”絵文字あり”の方が良い様に見えます。
この時、有意水準5%でこの差が有意であるかを検定してみましょう。
まず、各値から、全体のクリック割合を計算します。
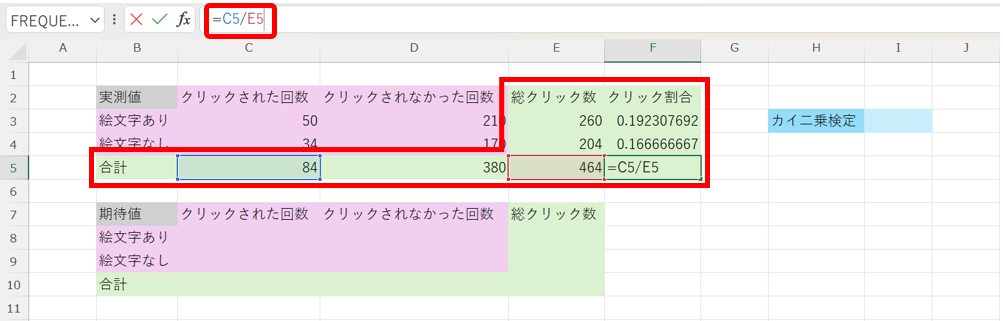
次に、「絵文字あり」でも、「絵文字なし」でも、全体のクリック割合に等しかった場合の期待値を計算します。
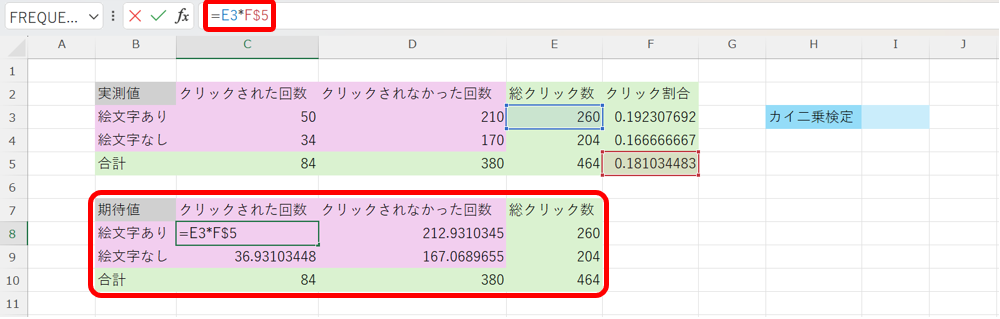
最後に、実測値と期待値を選択して、CHISQ.TEST関数でカイ二乗検定を行います。
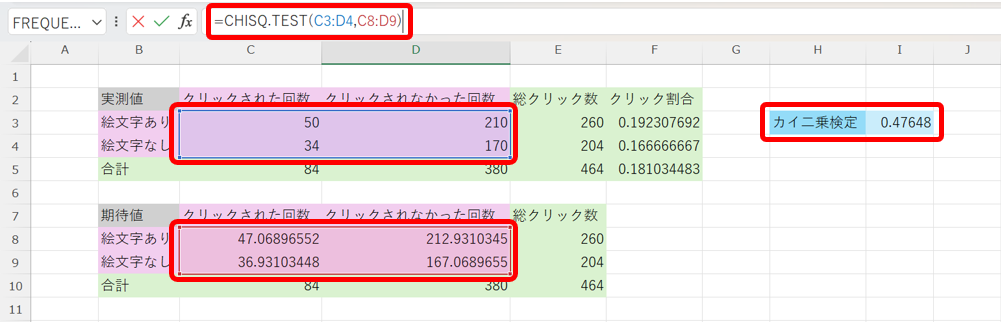
この結果から、カイ二乗検定のp値は約0.48であり、これは有意水準5%より大きいため、この差は有意ではないと判断できます。
F検定
続いて、F検定の例題もやってみましょう!
例題2(F検定)
C病院は、効果の高い解熱剤を求めて、A社とB社の解熱剤を比較しています。Excelファイル2ページ目のA社とB社の解熱剤の効果試験の結果から、2つの母分散が等しいかについて有意水準1%で仮説検定してみましょう。
F検定は、F.TESTを使ってしまえば、以下の様に非常に簡単です。
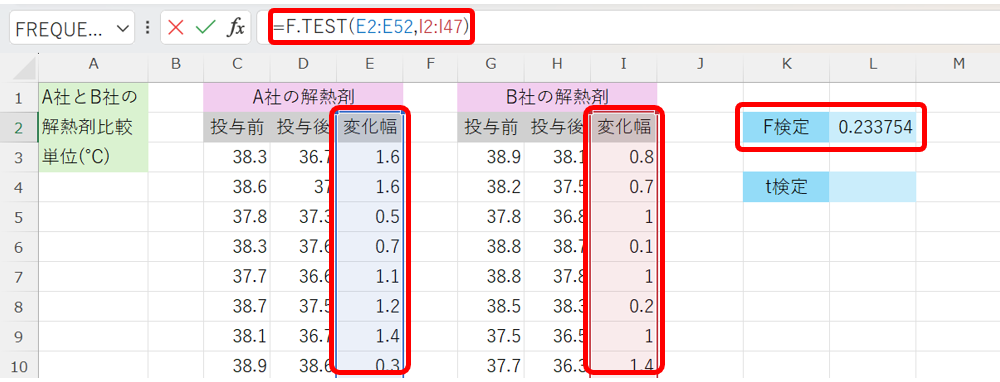
この結果から、F検定におけるp値が有意水準の0.05を超えている為、この2つの母分散は等しい(=等分散)とみなせます。
ちなみに、今回の問題は、第10章の対応のない場合の母平均の差の検定の問題です。
せっかく母分散[母標準偏差]が同じであると分かったので、これを使って母平均の検定を簡単に行ってみましょう!
例題2-1(対応のない場合の母平均の差の検定)
C病院は、効果の高い解熱剤を求めて、A社とB社の解熱剤を比較しています。Excelファイル1ページ目のA社とB社の解熱剤の効果試験の結果から、A社とB社の解熱剤の効果に違いがあるかについて有意水準1%で、母標準偏差が等しい場合と等しくない場合両方について仮説検定してみましょう。
ただし、母集団正規性は不明とします。
ここで、T.TEST関数を紹介します。
この関数の引数は以下の様になります。
=T.TEST(配列1,配列2,検定の指定,検定の種類)
まず、検定の指定に関して、以下の様に割り振られています。
| 引数 | 検定の指定 |
| 1 | 片側検定 |
| 2 | 両側検定 |
次に、検定の種類に関しては、以下の様に割り振られています。
| 引数 | 検定の種類 |
| 1 | 対応がある場合の母平均の差の検定 |
| 2 | 対応のない場合の母平均の差の検定(等分散) |
| 3 | 対応のない場合の母平均の差の検定(異分散) |
これを使って、例題2-1について、t検定を行っていきます。
まず、「A社とB社の解熱剤の効果に違いがあるか」なので、帰無仮説と対立仮説は
帰無仮説:A社とB社の解熱剤の効果に違いはない
対立仮説:A社とB社の解熱剤の効果には違いがある
となり、今回行う検定は両側検定です。
また、F検定の結果から、対応のない場合の母平均の差の検定(等分散)である事が分かります。
よって、t検定の結果は以下の様になります。
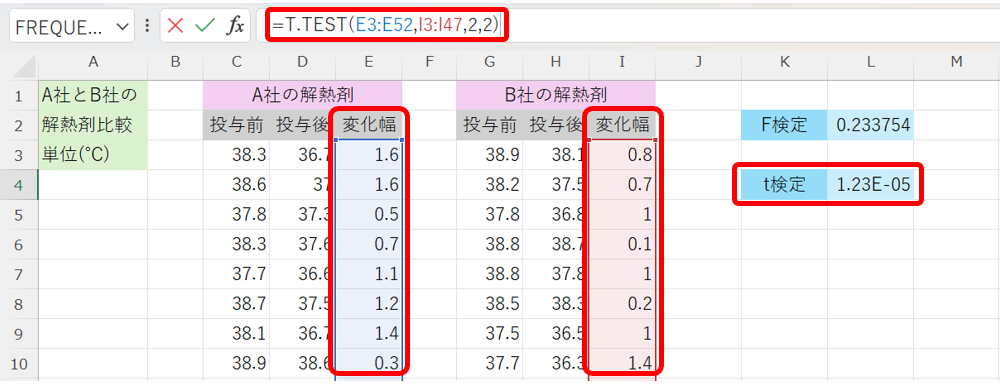
これより、t検定のp値が有意水準の0.05を超えていないので、この帰無仮説は棄却出来て、A社とB社の解熱剤の効果には違いがあると判断できます。
仮説検定方法まとめ
最後に、第8章から本第10章までの仮説検定の簡単なまとめとして、各種検定とその検定方法についてまとめておきます。
実際に検定を行う際に是非参考にしてください!
| 検定 | 検定方法 |
| 母平均の検定(1つの母平均と比較値が異なるかについての検定) | z検定 or t検定 |
| 母平均の検定(2つの母平均が異なるかについての検定) | (z検定) or t検定 |
| 母比率の検定(1つの母割合と比較値が異なるかについての検定) | z検定 |
| 母比率の検定(2つの母割合が異なるかについての検定) | z検定 |
| 母分散の比の検定(2つの母分散が異なるかについての検定) | F検定 |
| 本当に有意な差であるかの検定 | カイ二乗検定 |
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
まとめ
今回のExcelによる統計解析講座第10章では、カイ( \chi^{2})二乗検定とF検定について解説しました!
正規性の検定(カイ二乗検定)や母分散の比の検定(F検定)は、非常に重要な検定で、
特にz検定は、t検定と並んで、頻出する検定ですので、理解しておきましょう!
次章では、複数のデータについて分析する、分散分析について解説していきます。
非常に実用的な分野なので、是非読んでいってください!