機械学習

ベイズ最適化とは何か？理論から実装まで解説！

  /

機械学習を学ぶ上で「ベイズ最適化」という言葉を見たり、聞いたりしたことはあるでしょうか。中には「ベイズ最適化」について調べても、全然わからなかった人もいるでしょう。

「ベイズ最適化」は初学者には難しい概念ですが、さまざまなところで応用される手法です。

本記事では、ベイズ最適化の概要やメリットを実際の実装例を通して説明します。

目次
  1. ベイズ最適化とは？
  2. ベイズ最適化のメリット
  3. Pythonによるベイズ最適化
  4. ベイズ最適化によるハイパーパラメータ探索
  5. まとめ

本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。
データサイエンス講座の
詳細を見る➡

ベイズ最適化とは？

まず、ベイズ最適化を説明する際に必要な、以下の3つの専門用語を解説します。

  • ブラックボックス関数
  • 獲得関数
  • ベイズ過程

ブラックボックス関数

ブラックボックス関数とは、入力に対して出力の関数値の情報のみが得られる関数を指します。具体的には、y = f(x)のような関数において、fの形や性質がわからない状態です。しかし、その入力xに対しては出力yを返すことができます。

ベイズ最適化は、このようなブラックボックス関数に対して、限られた観測データから関数の形を推定する方法です。いくつかの観測データの点を手がかりにして全体の関数の形を推定します。

獲得関数

獲得関数とは、ベイズ最適化において、次に評価すべき候補点を選択するための関数です。ベイズ最適化では、この獲得関数を最大化する点xを指定し、その点xでのブラックボックス関数の出力yを観測します。それによって得られた新しいデータを加えて、再び獲得関数を最大化する点xを指定します。このような手順を繰り返すことで、最適な解を探索します。

獲得関数の定義は複数あり、それぞれの状況で使い分けられます。

  1. 改善確率量(probability of improvement(PI))
  2. 期待改善量(expected improvement(EI))
  3. 信頼下限(lower confidence bound(LCB))
  4. トンプソン抽出(Thompson sampling(TS))
  5. エントロピー探索(Entropy Search(ES))
  6. 予測エントロピー探索(predictive entropy search(PES))

これらの獲得関数が最大化するとベイズ最適化は完了です。

ガウス過程

ベイズ最適化では、ブラックボックス関数がガウス過程に従うことを仮定しています。ここで、ガウス過程とは最適化によって得られた関数がガウス分布に従っていることです。

ベイズ最適化によって、ブラックボックス関数の式は推定されます。しかし、ここで得られた式はあくまで推定した式なので、本来の式とは誤差があります。この誤差がガウス分布内におさまっていることを「得られた関数はガウス過程にしたがっている」と表現します。

ベイズ最適化

以上、３つの専門用語を説明したので、最後にベイズ最適化を説明します。

ベイズ最適化とは、ブラックボックス関数の式を観測済みのデータから推定するための手法です。その際、ブラックボックス関数はガウス過程にしたがうことが仮定されていて、獲得関数が最大になるとベイズ最適化が完了します。

以下の図はベイズ最適化後のグラフです。

グラフ上にある、赤い点が事前に得られていたデータです。そして、青の線がベイズ最適化によって得られた関数です。この関数はあくまでも、推定されたものなので、正解の関数と誤差があります。その誤差の範囲は灰色の部分で表されています。

ベイズ最適化のメリット

ベイズ最適化のメリットは以下の3点です。

  • 連続的でない関数に適用できる
  • 最適解を比較的低コスト、短時間で見つけられる
  • 一貫した手法で最適化できる

連続的でない関数に適用できる

ベイズ最適化はブラックボックス関数が連続的でない場合にも適用できます。最適化の手法の中には、途中に微分が含まれているものがありますが、連続的でない関数に対して微分はできません。対して、ベイズ最適化は微分ができない関数にも適用できます。

最適解を比較的低コスト、短時間で見つけられる

ブラックボックス関数の候補が少なければ、全探索したとしても低コストで最適化されます。しかし、ブラックボックス関数の候補が大量にあると、すべてを試すのは現実的ではありません。ベイズ最適化は最適なブラックボックス関数の候補を低コストで推定できます。

一貫した手法で最適化できる

ベイズ最適化が使用される前は、どの関数がブラックボックス関数として最適であるかは、それぞれの専門家の知見によって判断してきました。そのため、どれだけ最適化されるかは個人の能力に大きく依存してきました。一方、ベイズ最適化は誰もが一貫した手法で推定するため、個人によって最適化の結果が大きく変わることはなくなりました。

Pythonによるベイズ最適化

では、実際にPythonを使ってベイズ最適化を行います。

Pythonでベイズ最適化をする際には、ガウス過程用ライブラリGPyとガウス最適化を行うためのライブラリGPyOptを使用します。また、matplotlibはグラフを図示するためのライブラリです。

まず、GPyをインストールします。

pip install GPy

その後、GPyOptをインストールします。

pip install GpyOpt

また、matplotlibもインストールします。（matplotlibの最新バージョンでは最後の図示ができないので、matplotlibのバージョンを3.1.3に指定しています。）

pip install matplotlib==3.1.3

その後、GPyとGPyOptをインポートし、これから考えるブラックボックス関数の正しい式と制約条件を与えます。

今回は、ライブラリGPyOptにもともと入ってる関数を例に進めます。

%pylab inline
 import GPy
 import GPyOpt

# これから考えるブラックボックス関数と制約条件を与える
f_true= GPyOpt.objective_examples.experiments1d.forrester()
bounds = [{'name': 'var_1', 'type': 'continuous', 'domain': (0,1)}]  # 制約条件

この関数を図示すると、以下のようになります。

f_true.plot()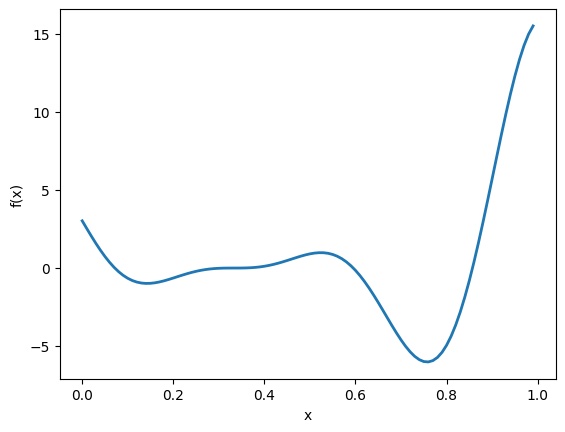

次にこれから最適化する関数を設定します。

# 統計モデルと獲得関数を設定します。
seed(123)
myBopt = GPyOpt.methods.BayesianOptimization(f=f_true.f, # 最適化する関数
                                             domain=bounds, 
                                             acquisition_type='EI',
                                             exact_feval = True)
 # 今回は獲得関数として期待改善量（expected improvement）を使用します。

実際にベイズ最適化します。

# 最適化を実行する
max_iter = 15 # 最大繰り返し回数
max_time = 60 # 時間予算
eps = 10e-6 # 2つの観測量の間の最小値

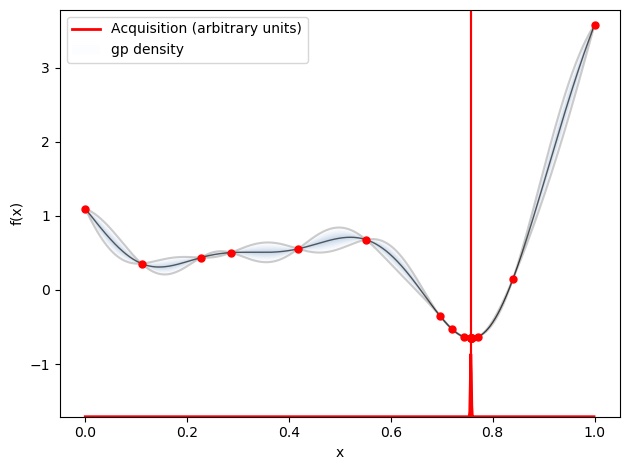
myBopt.run_optimization(max_iter, max_time, eps)

ベイズ最適化した関数を図示してみます。

myBopt.plot_acquisition()

このように、OPyとOPyOptを利用することで、Pythonでベイズ最適化が可能です。

ベイズ最適化によるハイパーパラメータ探索

ベイズ最適化は機械学習の中では、ハイパーパラメータ探索でよく使用される手法です。

ハイパーパラメータとは、学習を進めていくことで得られるパラメータではなく、事前に人の手で設定しておくパラメータです。

例えば、決定木における木の深さやリッジ回帰での正則化の強さなどがハイパーパラメータです。ハイパーパラメータの値の決め方は恣意的で、個人差があります。しかし、ベイズ最適化を利用することで、統計的にハイパーパラメータを決められます。

他にもハイパーパラメータの最適化の手段としてグリッドサーチがあります。グリッドサーチはハイパーパラメータ探索の手法としては、最も一般的です。グリッドサーチとはいくつかのハイパーパラメータのすべての組み合わせに対して交差検証を行い、最もデータにあったモデルを決定する手法です。

では、ベイズ最適化とグリッドサーチはどのような違いがあるのでしょうか？

１番大きな違いは、グリッドサーチは考えうる値を総当たりするのに対して、ベイズ最適化は一部の最適点のみを探索します。そのため、ベイズ最適化の方が、計算時間が短いです。
そのため、グリッドサーチはパラメータの数が少ない場合に使われることが多いです。

『Tech Teacher』3つの魅力

魅力1. オーダーメイドのカリキュラム

『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。

    魅力2. 担当教師によるマンツーマン指導

    Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
    東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
    そのため、理解できない箇所は何度も分かるまで説明を受けることができます。

    魅力3. 3,960円/30分で必要な分だけ受講

    Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。

    まとめ

    ・魅力1. 担当教師によるマンツーマン指導

    ・魅力2. オーダーメイドのカリキュラム

    ・魅力3. 3,960円/30分で必要な分だけ受講

    データサイエンス講座の
    詳細を見る➡

    30秒で完了！無料体験授業・資料請求はこちら➡

    質問のみのお問い合わせも受け付けております。

    まとめ

    ここまでベイズ最適化の説明をしてきました。

    ベイズ最適化とは、複数のデータの集合から目的関数を決定するための手法です。特に、機械学習の分野では、ハイパーパラメータ探索の際に使われることが多いです。

    また、ベイズ最適化はPythonに専用のライブラリがあるため、簡単に実装できるようになりました。

    ベイズ最適化を適切に利用して、より精度の高い機械学習モデルを実装できるようになりましょう！

    RELATED POST