主成分分析で情報の特性をグラフに表示できると聞いたことはあるけど、
多次元の情報を2次元に表示するなんてどうやってやるの?
そもそも主成分分析ってなに?
という疑問をお持ちの方はいらっしゃいませんか?今回はPythonで主成分分析をして次元削減をし、2次元のグラフで表現できるようにしていきましょう。
主成分分析とは
主成分分析とは、複数の変数を少ない変数で説明できるように情報を少数の軸に集約する方法で、分野によっては「マトリックス・データ解析法」と呼ばれることもあります。
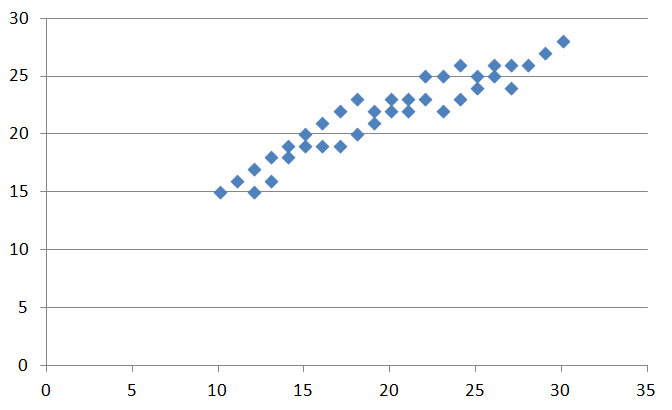
上の画像を見てください。データのばらつきを散布図にしたものです。このデータはx、yの数値で説明ができそうです。
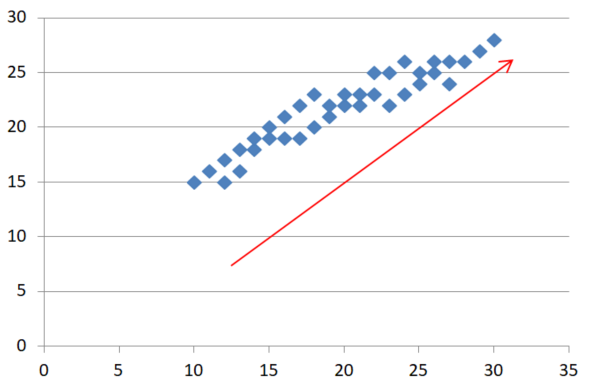
主成分分析は、この情報を少ない軸で説明できるように新しい軸を探します。上の図を見てください。赤い軸で軸を取り直せば右上に上がる軸が多くの情報を持っており、この1軸だけで元のx軸より多くの情報を説明できそうです。
主成分分析では多くの場合このように情報を多く持った軸に注目し、特に3次元以上のデータに関しては人間が見て理解しやすい2次元のグラフに落とし込んでやることができます。
このように、少ない情報軸に情報を集約し、不要な情報軸(次元)を削減していくことを「次元削減」といいます。これは上記のように人間に見やすいように2次元グラフ化するメリットだけでなく、計算コストを削減することにも役に立ちます。
Sklearnで主成分分析をしてみる
Pythonで主成分分析を行いたい場合、scikit-learnという非常に便利なライブラリがあります。このライブラリを使用すると非常に簡単に主成分分析を行うことができます。
今回は公式のドキュメンテーションでも解説に使用している、有名な「あやめデータセット」を使用して主成分分析の方法を解説していきます。初めて主成分分析をする方にも理解しやすいように難しい方法は省き、理解しやすさを第一に解説してみたいと思います。
scikit-learnとは
Python用機械学習ライブラリでだれでも使用できます。サンプルのデータセットから機械学習のライブラリまで豊富にそろっているので非常に便利なライブラリです。
事前準備
scikit-learnを使用する前に、事前準備をします。
scikit-learn以外のライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import pandas as pdデータアレイを扱うので「numpy」、データを確認するためにグラフを描きたいので「matplotlib.pyplot」、高次元データを取り扱うのでデータフレームを扱える「pandas」をインポートしておきます。
scikit-learnをインポートする
from sklearn.datasets import load_iris「iris(あやめ)データセット」を使用するため、「load_iris」をインポートします。
from sklearn.decomposition import PCA引き続き主成分分析をするため「PCA」をインポートします。ちなみに、主成分分析は「Principal Component Analysis」なので、PCAと略します。
データをロードする
iris = load_iris()データを読み込みましたが、このデータの中身を確認しておきましょう。
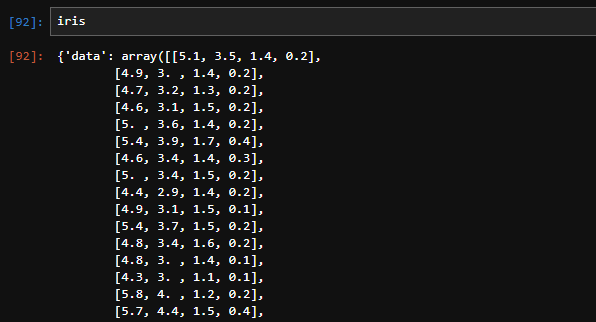
図のように「iris」と打って中身を確認すると、いろいろなことがかかれています。まず最初に出てくるのはデータ本体です。「array」形式でデータがずらっと並んでいます。
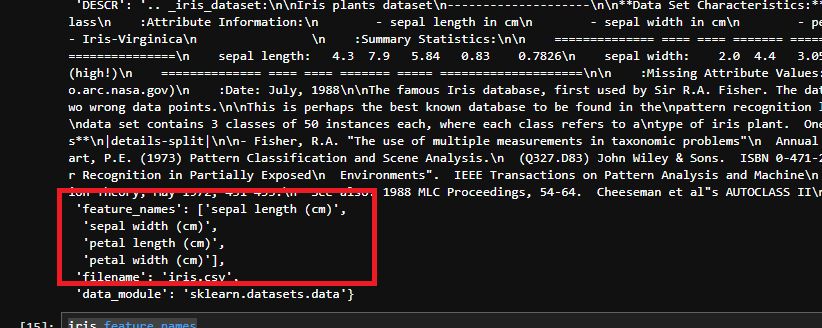
その次を見ていくと「target」データなどが並んでいます。このそれぞれのデータですが、以下のようにして情報を取り出すことが可能です。まずは「feature_names」の項目を取り出してみましょう。
iris.feature_names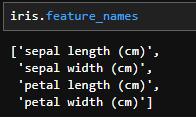
このように情報を取り出すことができました。
データの内容を眺めてみる
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
print(iris_df.head())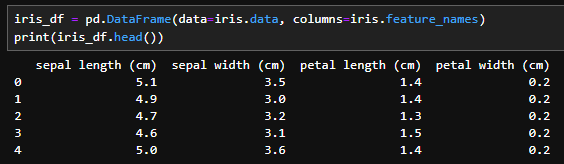
データにカラムをつけてみます。各カラムの内容は以下の通りです。
- sepal length (cm):がくへんの長さ
- sepal width (cm):がくへんの幅
- petal length (cm):花びらの長さ
- petal width (cm):花びらの幅
の4つの情報が変数の情報として与えられてます。
iris.target_names
次にターゲットの内容を確認します。
- setosa:ヒオウギアヤメ
- versicolor:ブルーフラッグ
- virginica:アイリス・バージニカ
各、あやめの名前です。
このデータセットはがくへんの長さ・幅、花びらの長さ・幅から、そのアヤメがヒオウギアヤメ、ブルーフラッグ、アイリス・バージニカのどれなのかを推測するものです。
iris.DESCR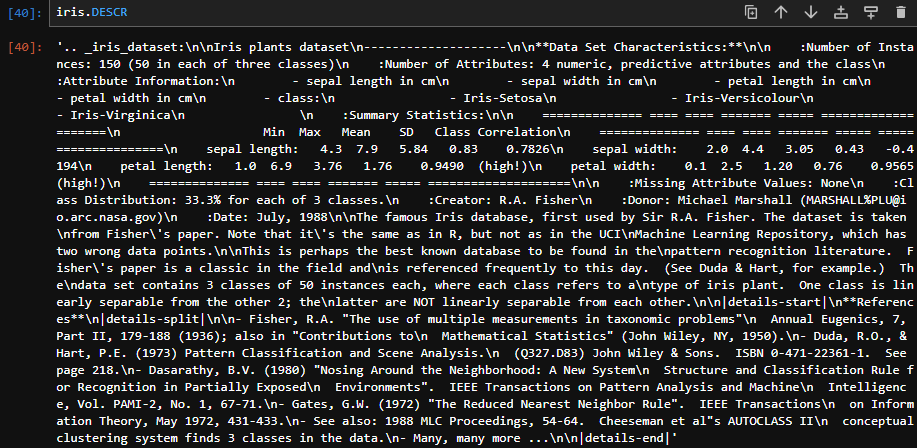
なお、参考ですが上記のように「iris.DESCR」を表示するとこのデータセットについて解説を見ることができます。
元データを作成する
x = iris.dataまずxに「iris」の「data」を設定します。これはデータの確認のところで作成したデータ同様
x = pd.DataFrame(data=iris.data, columns=iris.feature_names)としてもかまいません。
PCAの計算をする
pca = PCA(n_components=2)
tran = pca.fit_transform(x)
df_tran = pd.DataFrame(tran, columns = ['com1','com2'])
df_tran['target'] = iris.target
df_tran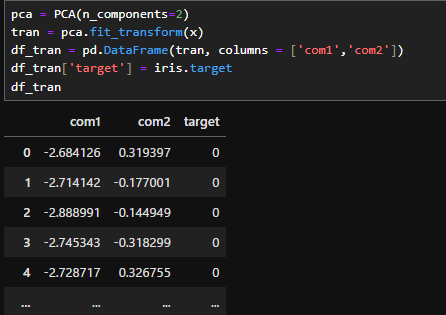
PCAの計算は非常に簡単です。まず、1行目でPCAを「pca」という名前で使えるようにします。その際、( )の中で第何主成分まで計算するかを入力します。今回はグラフに欠けるように第二主成分まで算出したいため、「n_components=2」とします。これを指定しない場合は入力と同じ、今回の場合は第四主成分まで計算します。
次に2行目でfit_transformをしてやると主成分分析後のデータに変換できます。
今回は三行目でデータフレームに変換、カラムをつけて見やすくしたのち、四行目でターゲットの情報をつけて、主成分分析後のデータとあやめの種類を一覧にしています。
targetの種類ごとのデータに分ける
グラフ表示の準備としてデータをtargetの種類ごとに分けます。この先の内容は実施しなくてもグラフ表示の際に指定すれば同じことができますが、あまり慣れていない方のためにわかりやすく解説するために事前に分割しておきます。
df_tr_0 = df_tran[df_tran.target == 0]
df_tr_1 = df_tran[df_tran.target == 1]
df_tr_2 = df_tran[df_tran.target == 2]グラフを表示する
plt.scatter(df_tr_0['com1'], df_tr_0['com2'], color='Blue' , label = "setosa" )
plt.scatter(df_tr_1['com1'], df_tr_1['com2'], color='Red', label = "Versicolour")
plt.scatter(df_tr_2['com1'], df_tr_2['com2'], color='Green', label = "Virginica")
plt.title( "2-D PCA of the 'Iris dataset'")
plt.xlabel('com1')
plt.ylabel('com2')
plt.legend()
plt.show()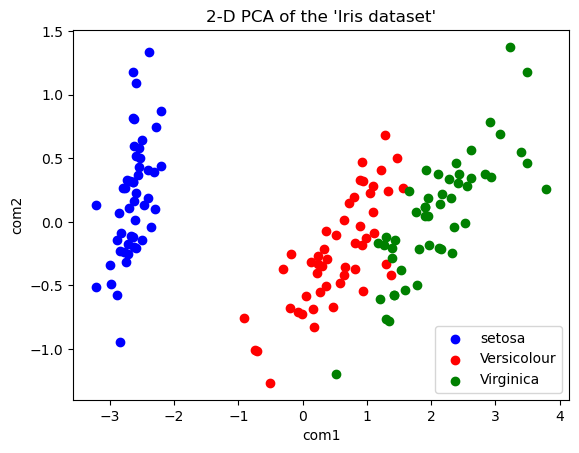
これでグラフが表示できました。もともと4次元の変数でしたが、主成分分析をすることにより2次元に圧縮しても元のデータの特性を保持していることがわかりました。
なお、このグラフはx軸が第一主成分、y軸が第二主成分となるため、x軸が一番多くの情報を持っており、確かにこのグラフではx軸だけでもおおよその分類は可能なようです。
ここまでのコードをまとめておきます。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
iris = load_iris()
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
# ターゲット(クラスラベル)をデータフレームに追加
iris_df['target'] = iris.target
print(iris_df.head())
print(iris_df.tail())
x = iris.data
pca = PCA(n_components=2)
tran = pca.fit_transform(x)
df_tran = pd.DataFrame(tran, columns = ['com1','com2'])
df_tran['target'] = iris.target
df_tran
df_tr_0 = df_tran[df_tran.target == 0]
df_tr_1 = df_tran[df_tran.target == 1]
df_tr_2 = df_tran[df_tran.target == 2]
plt.scatter(df_tr_0['com1'], df_tr_0['com2'], color='Blue' , label = "setosa" )
plt.scatter(df_tr_1['com1'], df_tr_1['com2'], color='Red', label = "Versicolour")
plt.scatter(df_tr_2['com1'], df_tr_2['com2'], color='Green', label = "Virginica")
plt.title( "2-D PCA of the 'Iris dataset'")
plt.xlabel('com1')
plt.ylabel('com2')
plt.legend()
plt.show()表示したグラフについて考える
次元削減について考える
以前にも説明しましたが、主成分分析自体は次元を削減するのではなく、あくまでも多くの情報をもっている新しい軸を探し出してやるだけで、今回主成分分析を行ってわかったように出力される情報の次元も入力した情報の次元と同じです。この中から持っている情報量の多い主成分だけを採用して次元を削減しているわけです。
そう考えると、今回採用しなかった主成分は本当に採用しなくてよかったのでしょうか?
寄与率を見る
新しく主成分分析で出した軸である各主成分が、元の情報の情報量をどれだけ持っているかを示すのが「寄与率」です。
今回の例で考えると、もともとirisのデータセットは、データを確認する項目でも出していますが、「iris.feature_names」の4項目の情報で「target」が0~2のどこに分類されるかを見ていました。この「iris.feature_names」4項目が持っていた情報を100と置いたときに、新しく出てきた「第一主成分」「第二主成分」「第三主成分」「第四主成分」がそれぞれその情報の何パーセントを持っているか、というものを示しています。
また、特定の主成分、例えば第三主成分までで何パーセントの情報を持っているか、というのを「累積寄与率」といいます。これはその名の通り、各寄与率の和で求まります。第三主成分の累積寄与率は「第一主成分の寄与率」「第二主成分の寄与率」「第三主成分の寄与率」で求まります。
pca.explained_variance_ratio_
寄与率の求め方は大変簡単で、先ほど計算した「pca」が「explained_variance_ratio_」という情報を持っているので呼び出すだけです。
plt.bar(range(1,5),pca.explained_variance_ratio_)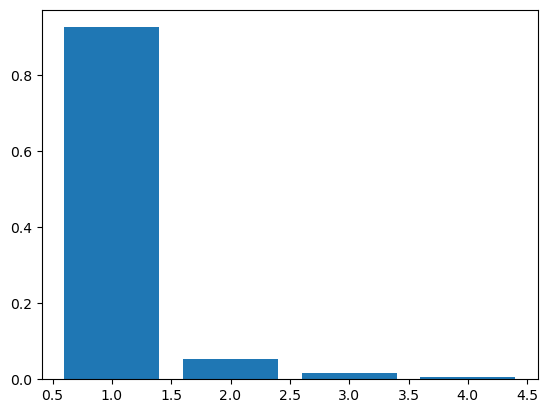
念のため、棒グラフでも表示しておきます。
これを見ると、第一主成分で92.5%もの情報を持っています。第三主成分と第四主成分合わせて2.2%程度しか情報を持っていないため、第二主成分まででグラフを描いても大丈夫そうですね。
【参考】第一主成分だけで見てみる
plt.scatter(df_tr_0['com1'], [0 for i in range(len(df_tr_0))], color='Blue')
plt.scatter(df_tr_1['com1'], [0 for i in range(len(df_tr_1))], color='Red')
plt.scatter(df_tr_2['com1'], [0 for i in range(len(df_tr_2))], color='Green')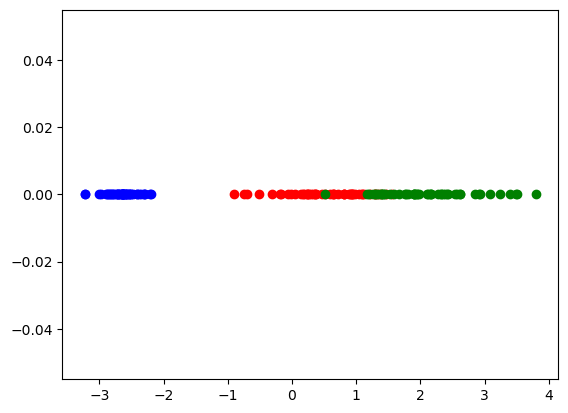
参考として、x軸上に配置することで、第一主成分だけでデータを表示してみました。確かに第一主成分だけでかなり大まかには分類ができそうですね。
固有値の求め方
pca.explained_variance_
固有値の求め方は上記の通りです。固有値は各主成分がどれだけ元データを説明できているかの値です。割合をとると寄与率になります。各コードの中にも出てますが、もともとバリアンス、分散の値です。分散が大きいほど値の変動が大きいので、主成分に対して情報の変動が大きいほど情報を多く持っている、ということですね。
固有ベクトルの求め方
pca.components_
次は固有ベクトルです。各主成分が元のデータをどの程度表しているかがわかります。arrayの形ではわかりにくいので、データフレームに変換し、columns、indexをつけてみます。
pd.DataFrame(pca.components_.T, index=iris.feature_names, columns=['com1', 'com2', 'com3', 'com4'])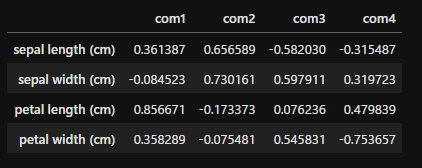
この値に固有値の平方根をかけたものが主成分負荷量です。主成分負荷量の第一主成分、第二主成分をプロットすることにより、第一主成分、第二主成分と元の変数との関係が見えてきます。
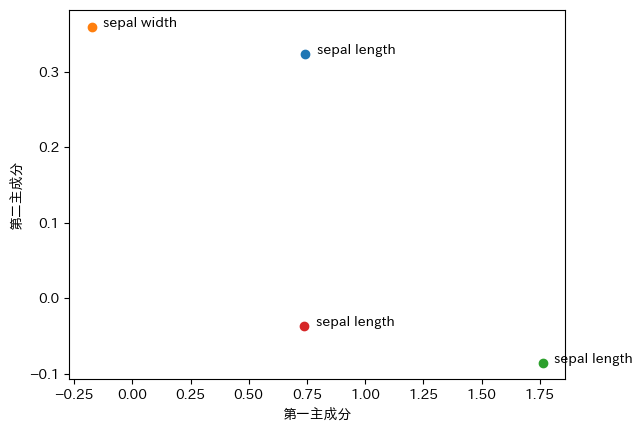
このように、元のデータとの関係をみてあまりにも実感とかけ離れていないか、かけ離れているとしたらなにが問題なのかを確認することも大切です。
以下の記事ではPythonでデータ分析をする方法について詳しく解説しています。
Pythonでデータ分析を行う方法は?おすすめライブラリも紹介!
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
まとめ
今回は主成分分析について解説しました。主成分分析の計算自体は非常に簡単に行うことが可能で、二次元まで情報を削減すればグラフに落とし込めるため非常に有効な分析手法です。
ただ、主成分分析はPythonで実行する際、勝手に決められた次元まで削減することもできるため主成分分析自体が次元削減をしていると誤解されている方が多いようですが、主成分分析はあくまでも情報量の多い新しい軸を探してやる作業です。寄与率などを確認し、どこまで削減してよいかなどを見極めたうえで活用するようにしてください。









