【１分でわかる】特徴量エンジニアリングの進め方

　ある程度機械学習の習得が進んでくると突き当たる壁、特徴量エンジニアリングですが

　という声は多いと思います。今回はこの特徴量エンジニアリングについて解説していきたいと思います。

本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。

データサイエンス講座の
詳細を見る➡

特徴量エンジニアリングとは？

　特徴量エンジニアリングとは、機械学習の精度向上のために特徴量を検討する作業です。そもそも準備したデータはデータを説明するに足るデータなのか、不要なデータは入っていないかなどを確認しモデルの精度向上を狙います。

なぜ特徴量エンジニアリングが重要なのか？

不要なデータ

　データを分析する際、単純に手持ちのデータをすべてモデルに投入するようなことを行っていませんか？データ分析コンペやscikit-learnのデータセットはあらかじめ関係あるデータがまとまっているのでこのようなことをやりがちですが、実際のデータ分析の際は必ずしも関係のあるデータばかりであるとは限りません。

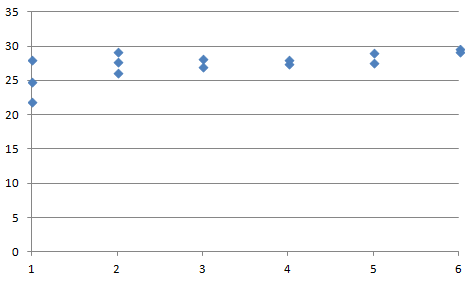
　例えば上のグラフを見てください。なんとなく相関関係がありそうで、このX軸のデータを使ってY軸のデータが予測できるかもしれません。・・・本当にそうでしょうか。

　実はこのデータ、東京の23年9月の平均気温を縦軸、横軸に平均気温のデータ数と同じ回数だけサイコロを振って並べたものです。普通に考えてサイコロから気温を予測することはできませんね。今回は非常にわかりやすいデータですが、このように明らかに関係ないデータを解析から取り除くことは重要です。

重複しているデータ

　例えば外気温と湿度、最高気温とアイスの売り上げに関するデータがあったとします。その際、３つの特徴量から売り上げを予測するモデルを作成する場合、外気温、湿度、最高気温の情報をそのまま特徴量として使用してもよいものでしょうか。

　そもそも外気温と湿度には関係がありそうですし、最高気温と外気温も関係がある場合がありそうです。外気温と湿度の相関が高いことを多重共線性といいますが、このような場合うまく予測できないことがわかっています。（理由や対策は後の解説で説明します）

特徴量エンジニアリングでどのようなことをするの？

　特徴量エンジニアリングではこのような特徴量が、予測したい予測値をうまく説明できるかを検証するとともに、特徴量として問題がある場合はそれを問題ない形に変形したりして特徴量として利用できる形に変形したりします。

手法に入る前に

ドメイン知識

　特徴量エンジニアリングでデータの加工技術を学ぶことは重要ですが、それと同じくらい重要なのがドメイン知識です。ドメイン知識とは「その分野に関する知識」のことです。

　先ほどの例でいうと、アイスの売り上げは気温と相関関係があることがわかっています。ということは、データを見た際にこれと違う結果が出ているようであれば何かが間違っているのか、もしくは別の情報が不足していないかを確認してみる必要がありそうですね。

　このように、実感とそぐわない結果が出てきたときにデータやモデルが間違っていないか、もしくはそれが事実なのかを見極めるためにもドメイン知識は重要です。

データ把握

　手元にあるデータセットがどのように集められ、どのような特性を持っているかを知っておくことも重要です。

　自分でデータを収集している場合は問題ないと思いますが、誰かがデータをとった場合、同じ条件でとっているか、正しくデータをとっているか、データをとった人は趣旨を理解しているかなど確認しておくとよいと思います。

特徴量エンジニアリングの進め方

特徴量エンジニアリングの前処理

　特徴量エンジニアリングについて、具体的な例としてscikit-learnの「iris」データを使用して具体的に見ていきましょう。

　事前に説明用のデータを以下のように用意しました。scikit-learnやirisデータの詳細に関しては別記事を参照してください。

import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df_y = pd.DataFrame(iris.target, columns=['target'])
df = pd.concat([df, df_y], axis=1)
df.head()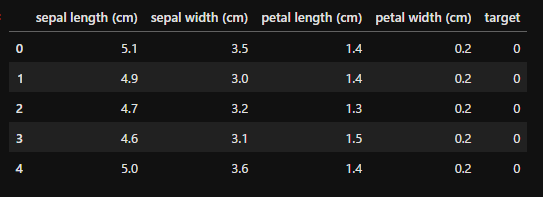

欠損値

　まずはデータに欠損値がないか確認します。データに欠損値が含まれていると、モデルによっては解析できないだけでなく、データの意味が変わってしまうこともあります。そのため、欠損値がないかを事前に確認します。

　以下のようにすることで各カラムごとの欠損値（データがない部分）の確認ができます。

print(df.isnull().sum())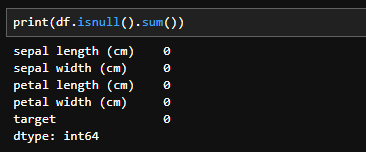

　データに欠損値が存在する場合、以下のような対応をします。

• 欠損値を含むデータを削除して解析する
• 欠損値を「そのほかのデータの平均値」で埋める
• 欠損値を「すべて０」で埋める

　どのような対応をするかはデータ量や、そのデータの特性を考慮して決定します。

外れ値

　次に外れ値を確認します。ほかのデータより大きく外れた外れ値は、そのデータの特性を変えるだけでなく、モデルの精度を下げる原因にもなります。

　また、データにもよりますが機械学習のモデル学習時、一般的には外れ側のデータを多くく学習しない方がよい予測精度が出る傾向にあるため、外れ値によっているデータは排除しておく方が無難ではあると思います。

　こちらは以下のようにボックスプロットでデータ確認します。

plt.boxplot(df['sepal length (cm)'], labels=['sepal length'])
plt.ylabel('[cm]')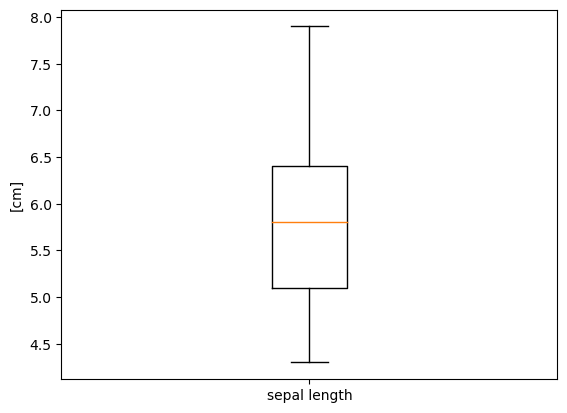

もしくは下記のように散布図を描くのもよいと思います。

plt.scatter(range(len(df)), df['sepal length (cm)'])
plt.title('')
plt.xlabel('Index')
plt.ylabel('sepal length (cm)')
plt.show()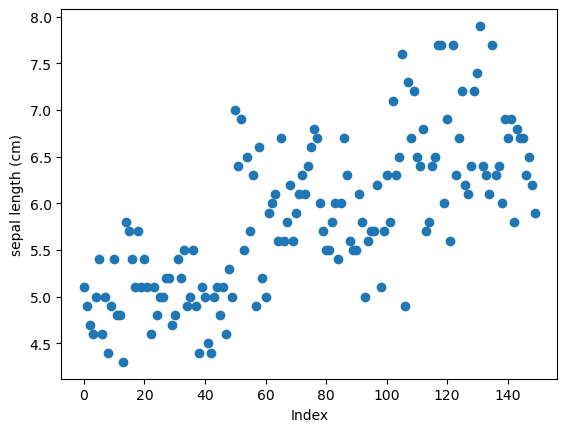

　この確認で外れ値がある場合は、その対象データの内容を確認し、削除しても問題なさそうであればデータを削除します。

特徴量の検討

　目的とする変数に対して、正しい特徴量を選択することは重要です。桶屋の売り上げを求めるのに風速を特徴量として選択するのは実際にはよい選択とはいいがたいです。

　では、その特徴量をどのように選択するとよいかについて考えてみます。

相関と疑似相関

　前述の通り特徴量は、データセットの段階では特徴量として意味を成しているのか否かがわかりません。既出の外気温と加工精度の問題のように、一見して関係性がありそうでも実は関係性がないこともあります。

　そのため、その特徴量と目的変数に関係性があるかどうかを見る指標に「相関係数」があります。相関が高い特徴量を選択することはモデルの精度アップにつながりそうです。

df.corr()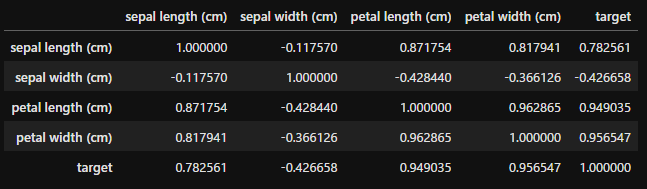

　相関係数は上記のように算出でき、

• -0.7以下：強い負の相関
• -0.7～-0.3：弱い負の相関
• -0.3～0.3：ほぼ無相関
• 0.3～0.7：弱い正の相関
• 0.7以上：強い正の相関

　があるといいます。また、数値上は相関があるが、見せかけだけの相関であることを「疑似相関」といいます。

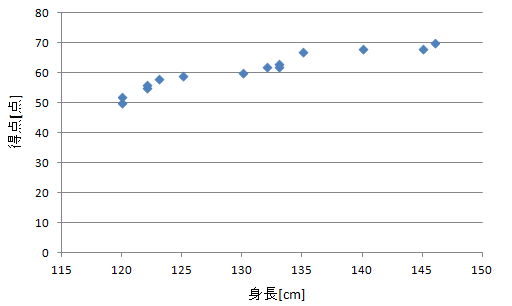
　例えばこのような有名な問題があります。上記のデータは身長とあるテストの得点を散布図で示したものです。これを見ると、身長と得点には相関関係があって、身長が高いほど得点は高くなりそうです。

　しかし、冷静に考えるとこのようなことはあるのでしょうか。実はこのデータはテストを受けた学年が混ざっており、高学年ほどテストで解ける範囲が多くなり点数が高く、また、身長が高いという一見して「身長」と「得点」に相関性がありそうなデータに見せかけて、実はそこには「学年」というものを介して相関があるという「疑似相関」の例になります。

　前述のドメイン知識を生かし、このような疑似相関を見抜くことも必要です。

多重共線性を排除する

　次に注目するのが多重共線性です。これは目的変数に対してではなく、特徴量間で相関係数が高いとデータの精度が向上しないというものです。これは「重複しているデータ」の項目でもありましたが、データの意味合いが近い特徴量が二つ存在すると、データの変動に非常に不安定になる傾向にあるので、このようなデータは特徴量として採用しないことを検討してみてください。

特徴量作成

　多重共線性を持つデータがある場合などに役立つのが、この特徴量作成です。複数の特徴量から一つの特徴量を作成してやることで、多重共線性を防ぐことが可能で、かつ、複数の特徴量がもつ情報を織り込むことが可能です。

　具体的には、たとえば先ほどの気温、湿度の例ですと気温と湿度から水蒸気量を出して特徴量にしたり、カテゴリーごとに平均値を出してその値をカテゴリーの代わりに特徴量として使用したりします。

Feature importance

　決定木系のモデルでは、分類時に特徴量が重要な役割をしたかどうかをしめすFeature importanceを表示できるものがあります。この指標を参考に、特徴量を入れ替えて精度が向上するかを試すことも有効です。

　Feature importanceを確認したのち、変数減少法で特徴量の数を減らして最も数値の良いところを採用するのがよいと思います。相関や、多重共線性のところで説明したように、見た目だけではわからない疑似相関や多重共線性がある場合があるので、実際に解析をしてみるのが一番良いと思います。

カテゴリー化・ワンホット化

　カテゴリーを数値で与えられている場合、それを各カラムにカテゴリー名をつけて1か0で示してやる方法をワンホット化といいます。アルゴリズムによってはワンホット化することによって精度が向上する場合があります。

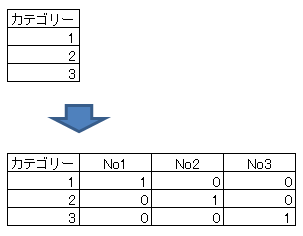
時系列データ

　データが時間の概念を持っている場合、例えばデータに周期性があったり時間ごとに数値が変化している場合、特徴量に現れない「時系列」という情報が隠れている場合があります。

　この場合は時系列自体が重要な場合は時間などの特徴量を別途作成したり、時系列が逆に重要でない場合は前後のデータとの平均をとることにより時間との関連性を薄くするなどの対応が考えられます。

まとめ

　今回は特徴量エンジニアリングについて説明しました。この分野は非常に奥の深い分野だと思います。テクニックだけではなく、ドメイン知識、データ理解も合わせて理解していただけるとよいかと思います。