【最重要】機械学習で不可欠な特徴量を完全理解！より良い設計を目指して

近年、多くの機械学習サービスがリリースされ、誰でも気軽に機械学習を使うことができるようになりました。そんな中、入力するデータを表現するために最低限用意しなければならないのが特徴量です。どのような特徴量を用いてデータを表現すれば良いか、悩んだ経験がある方も多いのではないかと思います。

この記事では、機械学習初学者の方を対象に、特徴量が機械学習手法の中でどのように利用されているのかを解説し、より良い特徴量設計に対するヒントを与えます。

特徴量とは？

特徴量とは、対象を表す一つの量です。

例えば、「人間の特徴量」について考えてみましょう。「人間」を表す一つの量には何があるでしょうか？身長、体重、年齢など、いくつか思い浮かぶと思います。そのどれもが特徴量であり、対象を表現すると思われるものであれば我々が自由に選んで構いません。

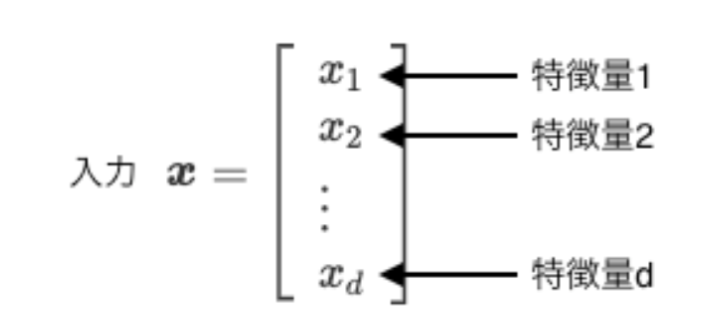
以下の画像のように特徴量を並べたものを、入力と呼び、太文字のxで表します。上の例で言うと、xが人間で、x1が身長、x2が体重といった具合です。

近年の機械学習サービスの中には、特徴量さえ用意すれば使えるものも多く存在します。しかしながら、期待した結果が得られない場合や、もっと性能を向上させたい場合には、与える特徴量について考える必要があります。これを「特徴量エンジニアリング」と言います。

では、何を基準に特徴量を選べば良いのでしょうか？以降の章で詳しく見ていきたいと思います。

特徴量エンジニアリングについては以下の記事で詳しく解説しています。

【１分でわかる】特徴量エンジニアリングの進め方機械学習でモデル精度を上げようとすると突き当たる特徴量エンジニアリング。重要であることは理解できるけどなんで？またどうしたらいいの？という疑問に答えていきたいと思います。...

教師あり学習

ここでは、機械学習手法の中でも特に「教師あり学習」について考えます。

教師あり学習では、大量の入出力ペアから、入力と出力の関係を学習します。出力が連続値の場合は回帰問題と呼ばれ、離散値の場合は分類問題と呼ばれます。入力と出力の関係を表現するために用いられるのがモデルと呼ばれるものであり、どのようなモデルを用いるかは機械学習手法によって異なります。

ここで、少しだけ記号を準備しておきます。多くの文献で入力は太字のx、出力はy、モデルはfで表されます。これらの記号を用いると、教師あり学習は大量の入出力ペア(x, y)からy=f(x)となるfを見つける枠組みになります。

先ほどの疑問である、何を基準に特徴量を選べば良いか？ですが、特徴量は入力の構成要素です。教師あり学習では入力から出力を予測するモデルと呼ばれるものを構築します。入力と出力の間に何の関係もなかったら、モデルの構築は難しいでしょう。

つまり、「出力との関係の強さ」が特徴量選択の一つの基準になります。実はこの「出力との関係の強さ」が数値として出てくる場合があります。次の章で詳しくみていきましょう。

モデル

複数の特徴量で構成される入力xは、モデルfに入力されます。モデルはパラメータを持ち、入力とパラメータを使って、出力yを計算します。パラメータは学習により調整されます。

最も基本的な「線形モデル」は以下のように表されます（θはパラメータ）。

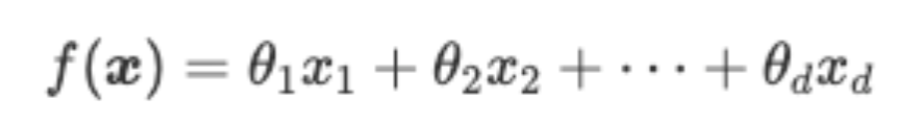
このように、線形モデルは特徴量とパラメータの積を足し合わせたものになっています。一つの特徴量に対して、一つのパラメータが割り当てられているというイメージです。ここで、モデルは出力を表現していること、y=f(x)、を思い出しましょう。

パラメータを調整するときに、大事なのは符号と大きさです。

まず、符号から見ていきましょう。分類問題の場合、出力は+1か-1です。簡単に、特徴量も+1か-1だとしましょう。出力と特徴量の符号が合っているとき、モデルは特徴量をそのまま出力すれば良いので、パラメータは+1に調整すれば良いことがわかります。一方、出力と特徴量の符号が逆の時、モデルは特徴量を反転して出力すれば良いので、パラメータは-1に調整すれば良いこともわかります。

次に、パラメータの大きさについても見ていきましょう。出力と符号が合ったり合わなかったりすると、パラメータを+1か-1のどちらにすれば良いのかわかりません。この場合、この特徴量を信頼して良いかわからないので、パラメータは0に近い値にせざるを得ません。

このように、パラメータθは前の章の最後に紹介した「出力との関係の強さ」を数値化したものになっています。特徴量x1と出力yの関係の強さはθ1で表されているといった具合です。

線形モデルを使った機械学習手法を使う場合、このパラメータを見ることで特徴量の取捨選択ができます。このように、自動的に特徴量の取捨選択を行う枠組みを特徴選択（feature selection）と呼びます。

特徴選択

最後に特徴選択手法を一つ紹介してこの記事を終えたいと思います。

前章で、線形モデルのパラメータは特徴量と出力の関係の強さを表現していると説明しました。これにより、パラメータが小さければ対応する特徴量を捨て、パラメータが大きければ対応する特徴量を採用する、といった特徴量の取捨選択が行えます。

このような処理を行うときには、この値より小さければ捨てて、この値より大きければ採用するといったような閾値を用意するのが一般的です。しかしながら、閾値をどのぐらいにすれば良いかは自明ではありません。

もし、パラメータが0ならば、対応する特徴量は線形モデルの出力に全く影響しないことを意味します。これを利用して特徴選択を行うのがLassoと呼ばれる手法です。

この記事では詳しく説明しませんが、Lassoではl1正則化により、パラメータが疎になります。疎というのは、0が多いという意味です。これを利用して、対応するパラメータが0である特徴量を捨てることで特徴選択を行えます。

特徴選択は、計算量を削減するだけでなく、不必要な特徴量をデータベースに格納しておく必要がなくなるので、空間の節約にもなります。

おわりに

この記事では、特徴量とは何か、そして特徴量がどのように使われているのかを通して、出力との関係が強い特徴量が望ましいことを説明しました。

今回扱った関係は「線形」の関係ですが、非線形の関係を測ることができる相互情報量などを用いた特徴選択手法も存在します。この場合、解釈は非常に難しいですが性能が上がることがあるので試してみるのもおすすめです。皆さんの特徴量設計のお役に立てれば幸いです。