機械学習

次元削減手法でデータを効果的に抽出！仕組みから実践まで解説！

  /

データの特徴量数が多くて、分析が困難であると感じたことはありませんか？今回ご紹介する次元削減は機械学習手法の1つで、データの隠れた特徴を抽出できるアルゴリズムです。

高次元の特徴空間に存在する複雑なデータ構造やパターンの理解を目的に、大学での卒業研究やビジネス分野での顧客分析に用いられます。また、次元削減は可視化や前処理、過学習の防止など、幅広い機械学習タスクにおいて重要な役割を持ち、モデルの精度向上に繋がるでしょう。

この記事では、次元削減の基本的な仕組みや利用方法、さらには主なアルゴリズムについて解説します。

目次
  1. 次元削減とは
  2. 次元削減のアルゴリズム
  3. 次元削減のプログラム例
  4. 次元削減の学習方法
  5. まとめ

本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。
データサイエンス講座の
詳細を見る➡

次元削減とは

概要と目的

次元削減について学ぶ前に、次元数とはデータの特徴量数のことです。複数の特徴量を持つ例として、身体測定における以下のようなデータが考えられます。

  1. 身長
  2. 体重
  3. 握力
  4. 視力

一般的に次元数の大きいデータは平面の2次元や空間の3次元上に描画できないため、可視化が困難です。加えて、次元数の大きいデータを取り扱うのは大変な労力が必要で、データの分析に適しません。

これを解決するために、「相関する値をまとめる」をコンセプトにした次元削減という手法が考案されました。少し考えてみると、身長と体重にはある程度相関がありそうですね。新しく身長と体重の平均を特徴として置き換えてみましょう。

  1. 身長と体重の平均
  2. 握力
  3. 視力

次元数が4から3に減少しました。特徴量をまとめて次元数を削減することで、データの可視化や分析を簡単にできるメリットがあります。次元削減はより膨大な次元を持つデータで、隠れた相関関係を見つけるアルゴリズムなので、積極的に活用してみましょう。

【最重要】機械学習で不可欠な特徴量を完全理解！より良い設計を目指してこの記事では、機械学習初学者の方を対象に、特徴量が機械学習手法の中でどのように利用されているのかを解説し、より良い特徴量設計に対するヒントを与えます。特に、どのような特徴量を用いてデータを表現すれば良いか、悩んだ経験がある方にぜひ読んでいただきたいです。...

社会での活用

次元削減を利用すると、大量の高次元データを視覚的に確認できるため、市場の分析やマーケティング戦略の策定の手助けとなる資料を作成できます。また、得られた特徴量は隠れたデータの関係性を意味することから、オンラインショップでのレコメンデーション機能が社会で活用される良い例です。

他の機械学習アルゴリズムと組み合わせることも効果的で、例えばシンプルな全結合層のモデルの入力に次元削減を行う方が精度の高い結果が得られる場合があります。この現象は、データの特徴を事前に抽出することの影響です。

注意点

機械学習での次元削減には大きく2つのアルゴリズムに分かれます。

  1. 自動的に特徴を抽出する
  2. 数学的にあらかじめ処理内容を指定する

機械が自動的に次元を削減する場合では隠れた関係性を発見する能力が高いものの、全く新しいデータの特徴が現れるため、人が結果から考察するのに不向きです。一方、あらかじめ処理内容を指定すると、説明性は高いですが、効果的な特徴量の組み合わせが判断しづらくなります。

次元削減のアルゴリズム

次元削減にはいくつものアルゴリズムがあります。

  1. 主成分分析（PCA）
  2. t-SNE
  3. Autoencoder

今回は上記の代表的な3つの手法の仕組みや特徴を見てみましょう。

主成分分析（PCA）

主成分分析（PCA: Principal Component Analysis）は多次元データの特徴を統計的な手法を用いて低次元に変換します。もっともイメージしやすい手法なので、身長と体重のデータ例で考えてみましょう。

身長と体重には相関関係があり、2つの平均も同様の関係にあると考えられます。主成分分析ではデータの特徴量から関係性の強さを表す寄与率を求め、主成分ごとに分類します。

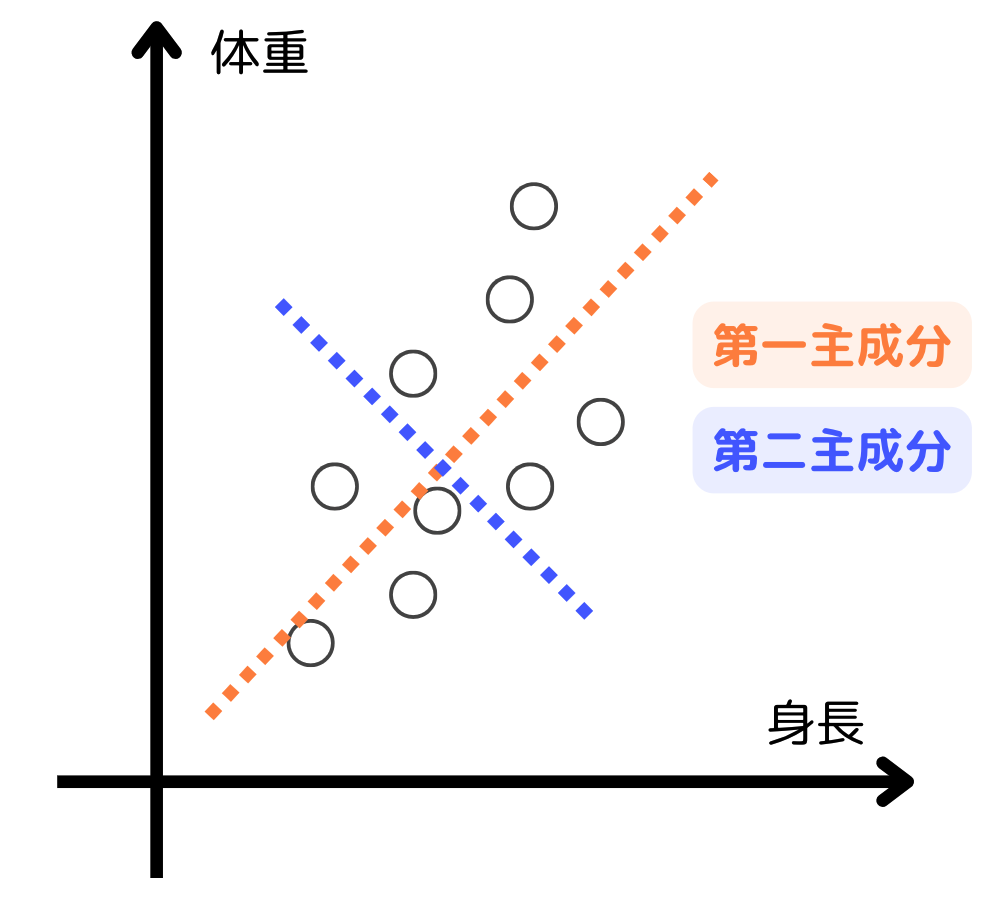
例えば、身長が寄与率60%の第一主成分、体重が寄与率40%の第二主成分のように分類されたとしましょう。次元分析では、身長と体重の関係性を考慮して新しい1つの特徴にまとめます。

以下が主成分分析の流れです。

  1. データを標準化
  2. 分散共分散行列の計算
  3. 固有値, 固有ベクトル分解
  4. 固有値の大きい順に固有値, 固有ベクトルを取得
  5. 主成分の決定

主成分が持つ情報量を大きくするため、共分散行列の固有ベクトルが主成分になります。このようにして、データから主な成分を抽出するアルゴリズムが主成分分析（PCA）です。図でイメージを持ちつつ、他のアルゴリズムとの違いを知ってみましょう。

【1分で理解】Pythonでの主成分分析の方法を解説！グラフ化で特徴把握PythonのSklearnを使用して、主成分分析を行って情報を二次元グラフに落とし込んで画像で見えるようにします。寄与率に関しても確認方法を見ていきましょう。...

t-SNE

t-SNE（t-distributed Stochastic Neighbor Embedding）は日本語ではt分布型確率的近傍埋め込み法ですが、一般的には略称で用いられる次元削減アルゴリズムです。

PCAは線型な次元削減手法だったのに対して、t-SNEは非線形な手法であるため、高次元データの特徴や類似性を非線形な関係性を保持しつつ低次元空間に落とします。これがデータの複雑な構造を保持できる理由です。

Autoencoder

自己符号化器（Autoencoder）はニューラルネットワークを基本構造とした次元削減手法の1つです。エンコーダとデコーダに分かれ、中間の層では潜在表現が得られます。

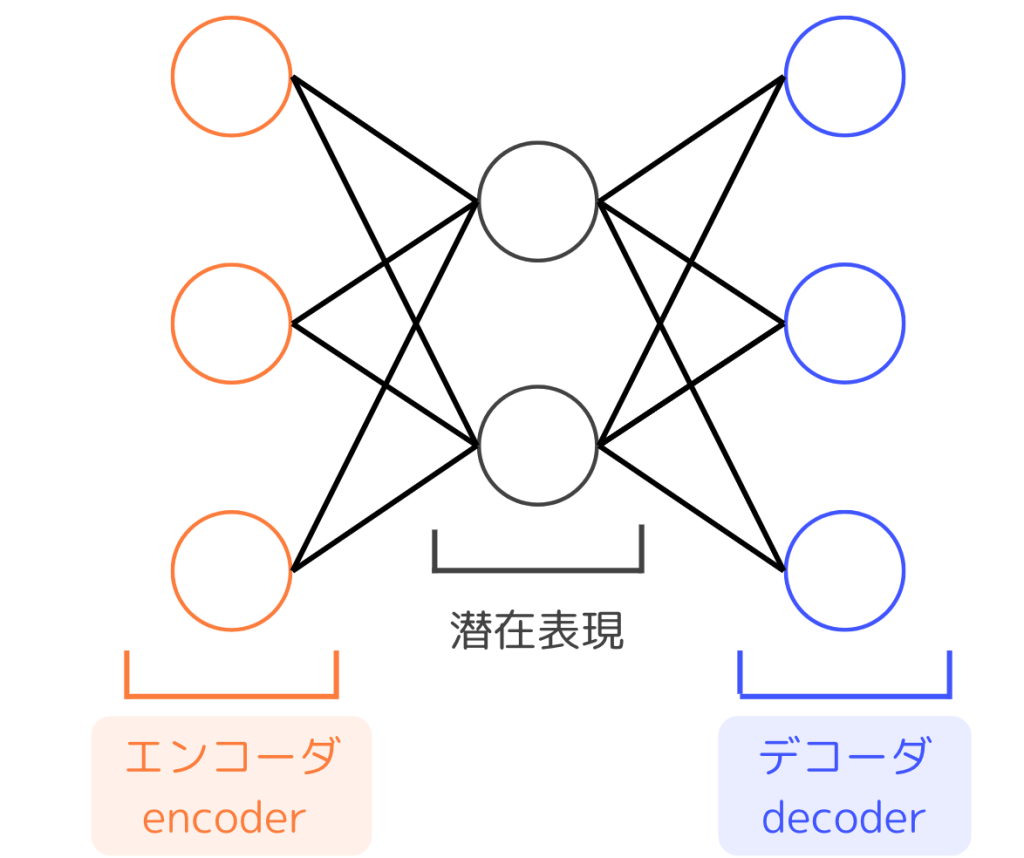
ネットワーク自体は通常の多層パーセプトロンと同じですが、入力層と出力層のサイズが等しく、隠れ層のサイズがそれよりも小さいことが特徴的です。

Autoencoderでは入力と同じ値を返すような学習を行い、より少ない次元数でデータの特徴を表す潜在変数を得ることを目的とします。イメージしやすい活用例は、画像データを3次元の潜在変数に変換することによる可視化です。

次元削減のプログラム例

データの可視化

次元削減により、2次元や3次元に変換すると、平面や空間上にデータを表示できます。隠れた関係性を可視化する手法であり、いくつかの手法が考えられます。

例えば、Autoencoderを用いて16次元の潜在変数を獲得して、それをPCAやt-SNEによって3次元のベクトルに変換することで、空間上に表示できます。

大規模なデータセットの場合は処理コストが大きく、膨大な時間が必要なことがあります。他のアルゴリズムに変更したり、次元数を調整することが有効的です。

プログラム例

Autoencoderを用いて手書き数字のデータセットであるMNISTデータの潜在表現を3次元空間上に描画するプログラムを実装してみましょう。本記事では、機械学習ライブラリのPyTorchを用います。


import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

# モデルの定義
class AutoEncoder(nn.Module):
    def __init__(self):
        super(AutoEncoder, self).__init__()
        self.encoder = nn.Sequential(
            nn.Linear(28*28, 128),
            nn.ReLU(),
            nn.Linear(128, 64),
            nn.ReLU(),
            nn.Linear(64, 3)
        )
        self.decoder = nn.Sequential(
            nn.Linear(3, 64),
            nn.ReLU(),
            nn.Linear(64, 128),
            nn.ReLU(),
            nn.Linear(128, 28*28),
            nn.Sigmoid()
        )

    def forward(self, x):
        encoded = self.encoder(x)
        decoded = self.decoder(encoded)
        return encoded, decoded

# データローダーの準備
transform = transforms.Compose([
    transforms.ToTensor(),
])

dataset = torchvision.datasets.MNIST(root='./data', train=True, transform=transform, download=True)
data_loader = torch.utils.data.DataLoader(dataset, batch_size=64, shuffle=True)

# 8つ画像を表示
def generate_images():
    with torch.no_grad():
        images, _ = next(iter(data_loader))
        images = images.view(images.size(0), -1)
        encoded, decoded = autoencoder(images)

    fig, axes = plt.subplots(1, 8, figsize=(12, 2))
    for i in range(8):
        axes[i].imshow(decoded[i].view(28, 28).cpu().numpy(), cmap='gray')
        axes[i].axis('off')
    plt.show()


# Autoencoderの学習
autoencoder = AutoEncoder()
criterion = nn.MSELoss()
optimizer = optim.Adam(autoencoder.parameters(), lr=0.001)

num_epochs = 3
for epoch in range(num_epochs):
    for data in data_loader:
        img, _ = data
        img = img.view(img.size(0), -1)
        _, recon_img = autoencoder(img)
        loss = criterion(recon_img, img)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    generate_images()

    print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# 潜在変数の表示
latent_vectors = []
labels = []

for i, data in enumerate(data_loader):
    img, label = data
    img = img.view(img.size(0), -1)
    with torch.no_grad():
        latent_vector, _ = autoencoder(img)
    
    latent_vectors.append(latent_vector.squeeze().cpu().numpy())
    labels.extend(label.cpu().numpy())

    if i > 10:
        break

latent_tensors = [torch.tensor(arr) for arr in latent_vectors]
latent_tensors = torch.cat(latent_tensors, dim=0)
labels_tensor = torch.tensor(labels)
unique_labels = np.unique(labels_tensor.numpy())

colors = plt.cm.tab10(np.linspace(0, 1, len(unique_labels)))
label_to_color = {label: color for label, color in zip(unique_labels, colors)}
point_colors = [label_to_color[label.item()] for label in labels_tensor]

fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
sc = ax.scatter(
    latent_tensors[:, 0], 
    latent_tensors[:, 1], 
    latent_tensors[:, 2], 
    c=point_colors, 
    cmap='tab10',
    s=50,
    label=labels_tensor
)

ax.set_xlabel('Latent Variable 1')
ax.set_ylabel('Latent Variable 2')
ax.set_zlabel('Latent Variable 3')

handles = [plt.Line2D([0], [0], marker='o', color='w', markerfacecolor=label_to_color[label.item()], markersize=10, label=f'Class {label.item()}') for label in unique_labels]
ax.legend(handles=handles, title='Classes')

plt.show()

コード量が多いですが、主な処理事項は以下の通りです。

  1. ライブラリのインポート
  2. Autoencoderモデルの定義
  3. データローダーの用意
  4. モデルの学習
  5. 潜在変数の可視化

プログラム例でのモデルは潜在変数を次元数5として取得し、そのうちの特徴量3つを空間上に描画します。では、実行結果にて生成された画像や可視化したグラフを見てみましょう。

実行結果

Autoencoderモデルが学習中に生成した画像です。潜在表現の次元数は3でしたが、ある程度数字の形を復元できていることがわかります。より高い精度のモデルを開発するには、モデルの構成を工夫したり、エポック数や最適化手法を調整することが必要です。

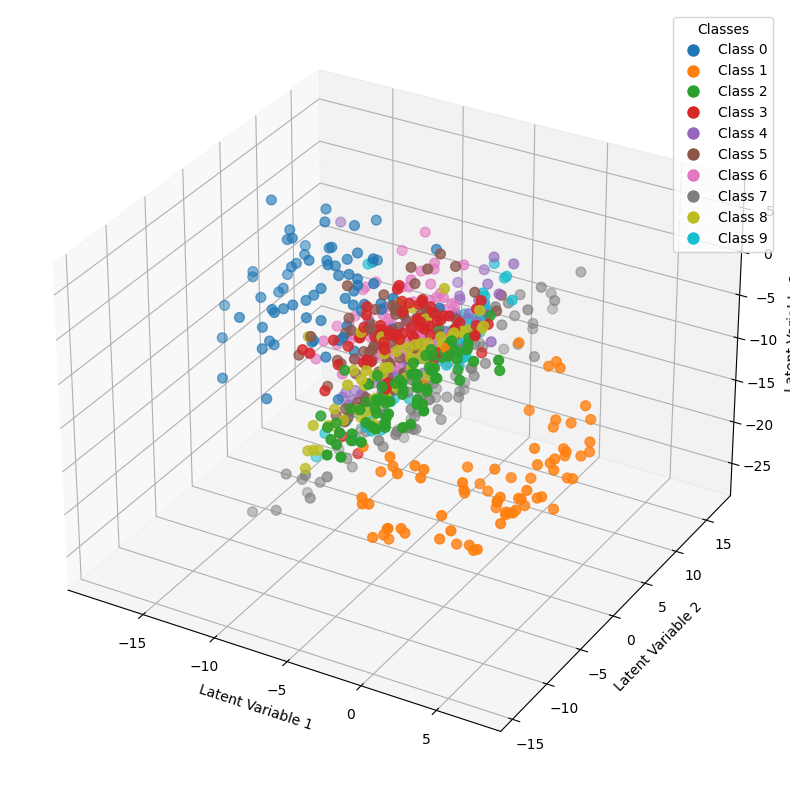
実際に潜在変数を3次元空間に描画した結果です。数字のクラスごとに色分けがされており、同じクラスに属するデータが綺麗に分かれていることが読み取れます。これはデータの隠れた関係性が現れており、MNISTデータの分析には低次元な隠れ層を持つautoencoderでも十分に効果的です。

次元削減の学習方法

次元削減の学習方法は目的によって異なりますが、主に数学とプログラミングを学ぶことが重要です。エンジニアとしてプログラム作成のみを目指す方であっても、ある程度は数学的な処理内容を把握しておきましょう。

数学

線形代数は主成分分析（PCA）などの次元削減手法に必須の知識であり、行列やベクトル、固有値や固有ベクトルなどに関する理解を深めることが求められます。数学を用いてアルゴリズムを明確なものにするため、ゼロから次元削減を実装したい方は数式で学習しましょう。

統計学での確率分布や期待値、分散などは次元削減だけでなく機械学習全般で必要な知識です。モデルの目的や、データの特徴を理解するために統計的概念を理解してみましょう。

プログラミング

コードの簡潔さやライブラリの豊富さから、機械学習では主にPythonが用いられます。本記事でのプログラム例ではPyTorchによるautoencoderモデルの実装をご紹介しました。

しかし、同じ処理をライブラリなしで実装することはほとんど困難であると言えます。複雑な配列操作や数式の表現は便利なライブラリを用いて、快適に機械学習の実装を行いましょう。

『Tech Teacher』3つの魅力

魅力1. オーダーメイドのカリキュラム

『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。

    魅力2. 担当教師によるマンツーマン指導

    Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
    東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
    そのため、理解できない箇所は何度も分かるまで説明を受けることができます。

    魅力3. 3,960円/30分で必要な分だけ受講

    Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。

    まとめ

    ・魅力1. 担当教師によるマンツーマン指導

    ・魅力2. オーダーメイドのカリキュラム

    ・魅力3. 3,960円/30分で必要な分だけ受講

    データサイエンス講座の
    詳細を見る➡

    30秒で完了！無料体験授業・資料請求はこちら➡

    質問のみのお問い合わせも受け付けております。

    まとめ

    次元削減はデータの隠れた関係性を得る機械学習手法でした。実際にPyTorchを用いてMNISTデータの潜在変数を可視化するプログラムでは、膨大なコード量でしたが、基本的なプログラムの組み合わせて実装されています。

    数学やプログラミングを学習して、大学の卒業研究やビジネスでのデータ分析にて、次元削減を上手に活用しましょう。

    RELATED POST