「クラスタリング」といえばKmeansを真っ先に思い浮かべる方も多いと思いますが、
Kmeansってなに?
クラスタリングってそもそもなんだっけ?
という方もいると思います。今回はクラスタリング、特にKmeansの内容からKmeansの実装、そしてそのほかのクラスタリングについても見ていきましょう。
クラスタリングとは
「クラスタリング」は、機械学習における「教師なし学習」の一つで、類似性でデータをグループ分けする方法です。クラスタとは集団やかたまりのことを意味します。データを集団に分けることでそのデータの属性、傾向を考察することができます。
クラスタリングには大きく分けて
- 非階層的クラスタリング
- 階層的クラスタリング
の2種類があります。非階層クラスタリングは事前にクラスター数を決め、クラスターへの分け方を決めたうえで、最適なクラス分けになるようにクラスター分けを行う方法です。一方階層的クラスタリングは類似度の近いものから順番にデータをまとめていく方法になります。</p
前者の代表的なものが今回説明する「K-means」、後者の代表的なものが「ウォード法」や「群平均法」です。今回はウォード法について階層型クラスタリングでよく使用するテンドログラムを用いて表現してみたいと思います。</p
k-means(非階層的クラスタリング)
非階層的クラスタリングで有名なk-means法ですが、Pythonで実装することも多いと思います。まずはk-means法がどのようなものかを見てみましょう。</p
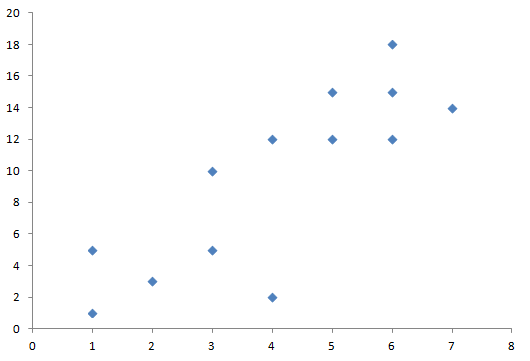
いま、ここに13個の点が存在します。これをk-means法で2つのクラスタに分けるとき、どのような手順をとっているかを見ていきます。
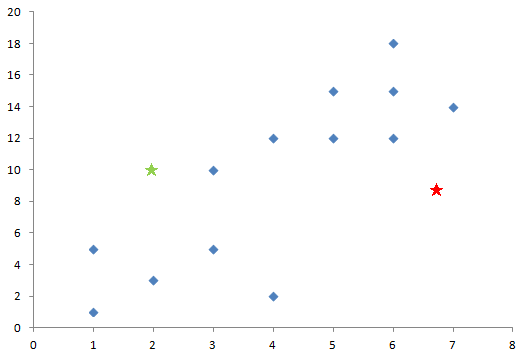
まずはクラスタの数だけ中心となる点をランダムに決めます。今回の場合、黄緑と赤の星の位置を選択しました。
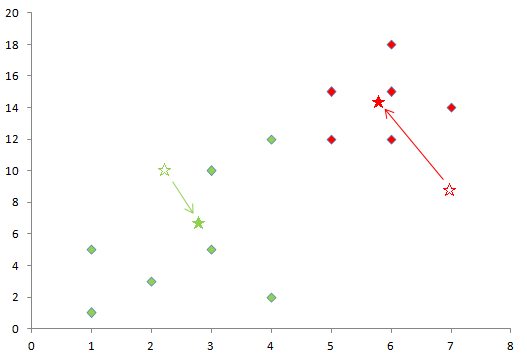
この中心点に対し、各点からの距離を計算し、もっとも近い位置の中心点と同じクラスターに各点を振り分けます。この図では各点を黄緑と赤のクラスターに分け、所属するクラスターの色を付けました。
その後、クラスター各点の重心をそれぞれ求め、その位置にクラスターの中心を移動させます。白抜きの☆から、★の位置に中心が移動しました。
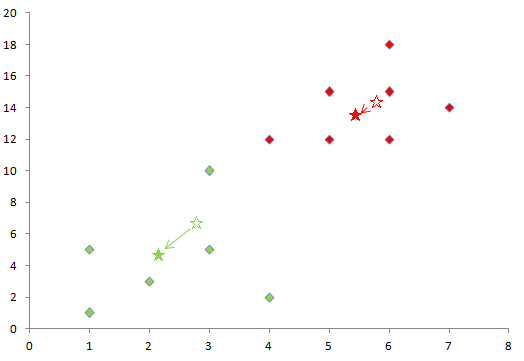
新しく中心が移動した場所で、再度各点を各クラスターに振り分け直し、またそのクラスターの重心を求めます。このようにしてか中心が最終的に移動しなくなるまで続け、クラスターを決定します。
k-meansを実装する
動作原理を見ると、何度も繰り返すのはめんどくさうと思ってしまいますが、scikit-learnを使用すると簡単に実装できてしまいます。
ここから実際にscikit-learnを使用してk-meansを実装してみましょう。コードを見やすくするためにまとめてコンパクトに書いてみましたので、その分解説を細かく書きます。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.datasets import load_irisまずは必要なライブラリーをインポートしていきます。
- グラフ描画:matplotlib
- 数値計算:numpy
- データフレーム:pandas
をそれぞれインポートします。
また、今回使用するk-means、そしてサンプルのデータとしてirisデータセットをインポートします。詳細に関しては他記事を参照してください。
data = load_iris()
df = pd.DataFrame(data.data, columns=data.feature_names)
df.head()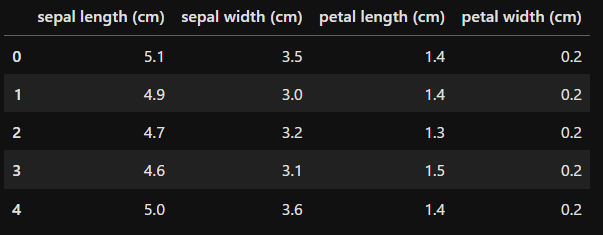
ここは「data」にirisデータセットを読み込んでいます。そのdataを使用して、dfというデータフレームを作成します。
今回は説明用にirisデータセットを簡単にデータフレームにしましたが、「【1分で理解】Pythonでの主成分分析の方法を解説!グラフ化で特徴把握」の記事の中でもirisデータセットの中身を細かく見ていますので、参考にしてみてください。

plt.xlabel('sepal length (cm)')
plt.ylabel('petal length (cm)')
plt.title('iris')
plt.scatter(df['sepal length (cm)'], df['petal length (cm)'])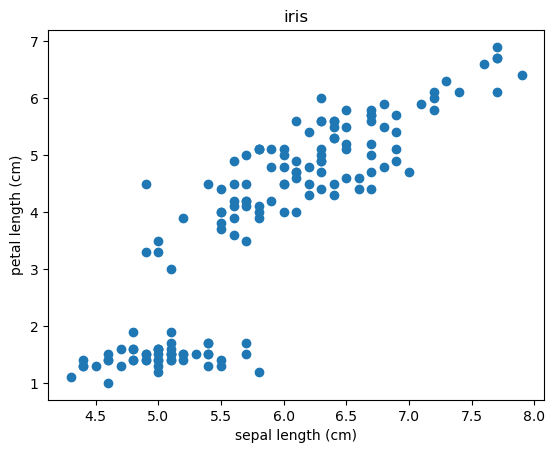
今回作成したirisデータセットは4つの特徴量(説明変数)を持っていますが、今回は「sepal length (cm)」と「petal length (cm)」の二つの特徴量でデータをクラスタリングしてみましょう。
まずはデータの状態を知るために、「sepal length (cm)」を横軸、「petal length (cm)」を縦軸において散布図を書いてみました。
km = KMeans(n_clusters=5, max_iter=30)
kmh = km.fit_predict(df[['sepal length (cm)', 'petal length (cm)']])
df['kmh'] = kmh
df.head()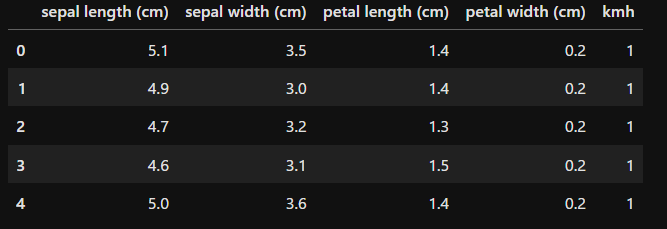
scikit-learnを使用すればk-meansでデータをクラスタリングするのは簡単です。
まずはモデルを読み込みます。変数は
- n_cluster:分割するクラスターの数
- max_iter:学習の反復回数の最大値
です。max_iterはこの値より早い段階で学習が終わった場合は早く終了します。
次にkm.fit_predict()で実際にクラスターに分けていきます。
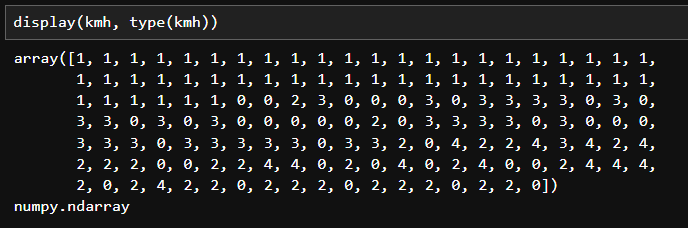
結果は上記の通り「numpy.ndarray」の形式で帰ってきますので、もとの「df」に追加しました。
plt.xlabel('sepal length (cm)')
plt.ylabel('petal length (cm)')
plt.title('iris')
for i in np.sort(df['kmh'].unique()):
plt.scatter(df[df['kmh']==i]['sepal length (cm)'], df[df['kmh']==i]['petal length (cm)'], label=f'cluster{i}')
plt.legend()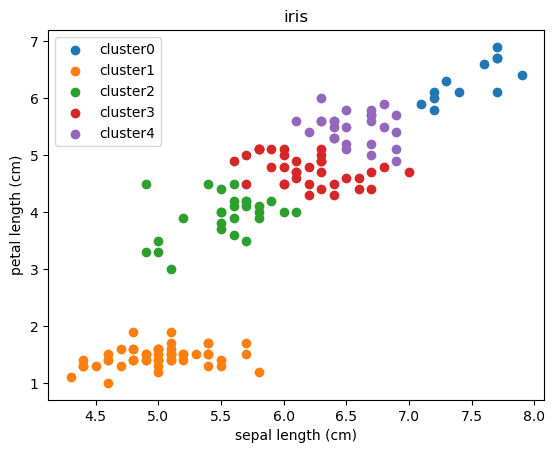
さて、数値で確認しただけではわかりにくいので実際に散布図にしてみましょう。
for文の部分ですが、dfの中のカラム「kmh」、先ほどの予測結果を入れたカラムにあるデータの種類を取り出して、0から順番に並べたものを順にiに入れています。今回の場合は0~4の数値が入っていますので、「0、1、2、3、4」と順番にiに数値が入ってforの部分が実行されます。
その後dfの中でkmhの値がiと一致するデータだけ取り出してプロットしています。
散布図を見ると近い部分のデータをクラスターとして取り扱っている様子がわかると思います。
階層的クラスタリング
機械学習でクラスタリングを行う際に、次に思いつくのがウォード法による階層的クラスタリングとテンドログラムでの表示でしょう。これについては「階層的クラスタリングとは? メリットや実装方法を丁寧に解説」でも解説しているので、合わせて確認いただけるとよいと思います。
ここではPythonを用いてテンドログラムに表現する方法を見ていきたいと思います。今回は先ほど使用したirisデータを使用しますが、全部をテンドログラムで表示すると細かくなってみにくくなるため、データを6個抜き出して表示してみます。
from scipy.cluster import hierarchy
linkage = hierarchy.linkage(df.iloc[[100,20,40,10,1,85]], method='ward')
hierarchy.dendrogram(Z=linkage)
plt.ylabel('euclidean distance')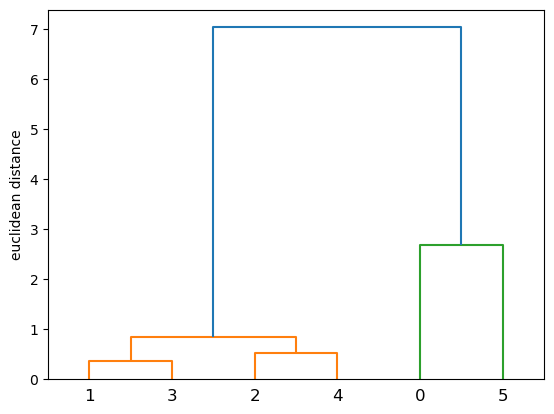
今回は「scipy」を使用しますので、この中から「hierarchy」をインポートします。
次に「hierarchy.linkage()」を読み込みます。データは先ほどのirisデータから手動で番号がばらつくように選んでみました。
引数にある「method=’ward’」はクラスタリングの方法を定義します。今回はよく使用される「ウォード法」を使用しています。そのほかには
- ward:ウォード法
- average:群平均法
- centroid:重心法
などがあります。
なお、ウォード法はクラスタ内の平方和を最小化する=分散を最小化することを目的として計算しています。
最後に結果の見方ですが、各データの配置されている位置と実際の近さには関係がありません。あくまでもy軸の距離を参照してください。
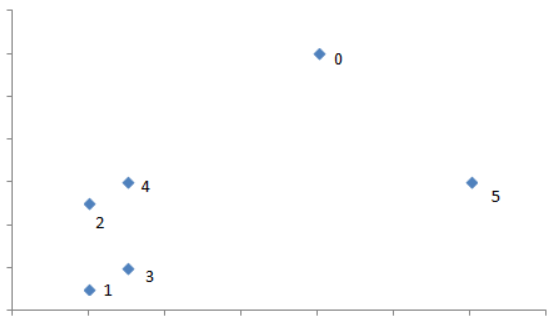
説明しやすくするために、距離は変えていますが上のような図を書いてみました。テンドログラムの横軸の関係でみると0と5のx軸の位置関係が「1と3」、「2と4」と同じなので「1,3」「2,4」「0,5」の組み合わせで見てしまいがちですが、上の図のように「1,3」「2,4」「0」「5」のクラスターや「1,2,3,4」「0」「5」のクラスターは考えられても「1,3」「2,4」「0,5」のクラスターは考えられません。必ずy軸で距離を見るようにしてください。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
まとめ
今回はPythonでクラスタリングする方法についてみてきました。クラスタリングは比較的簡単にできるので、今回の内容を参考にして実際に試してみていただければと思います。









