単回帰分析を最小二乗法をつかって解かないといけない課題などにあたったことはありませんか？
「そもそも最小二乗法ってなに？」
「linest関数ってどうやって使うの？」
このような疑問に答えるとともに、別の方法で問題を解決できないかも含めて解説していきたいと思います。
最小二乗法ってなに？
そもそも最小二乗法って何でしょうか。極力簡単に確認していきましょう。やってること自体は非常に簡単です。
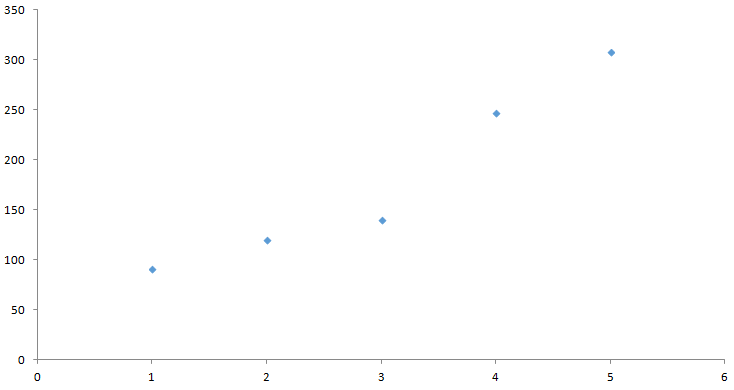
上の図を見てください。例えば、密度が不明な板があったとします。この板をいくつか測定して、長さと重さの関係を散布図にしてみました。密度一定なら本来比例の関係になるので一直線上に点が並ぶはずですが、密度が一定でないのか測定したときの誤差があるのか、一直線上に並んでいませんね。
この結果から長さと重さの関係を予測してみたいと思います。なんとなく、下図の赤線のような関係になりそうですが、どのように赤線を決めたらいいのでしょうか。
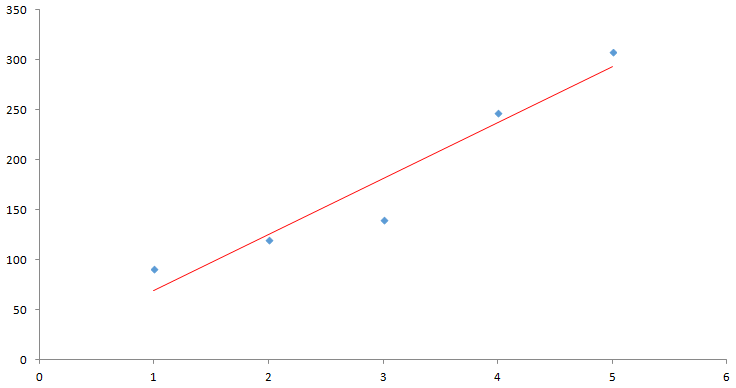
この赤線を求めるため、実際に測定した点と赤線から予測した点の距離をすべて足してこの距離が一番小さくなる線を考えればよさそうです。
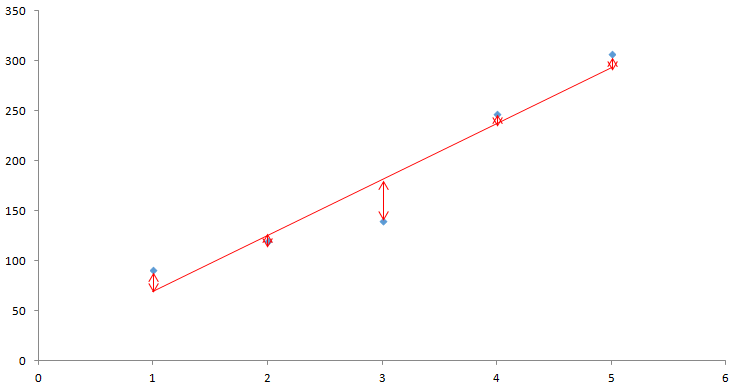
ただ、これをエクセルやプログラムで計算するために式にすることを考えます。そうしたときに各点と線の距離は下図のように
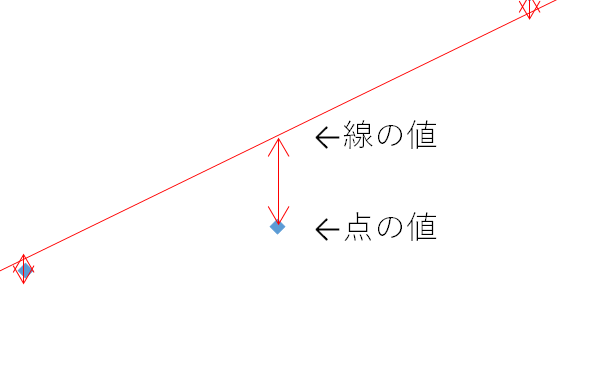
「線の数値ー点の数値」で表すことができます。ただし、ここで必ずしも線のほうが点よりも上にあるとは限らず、この出し方ではマイナスになってしまうこともあります。そのため「（線の数値ー点の数値）の２乗」をして必ず数値が正になるようにして各点の数値を足し合わせてあげています。この二乗にした距離の合計が最小になる直線を差が出すやり方、これが最小二乗法です。
エクセルでlinest関数を使用して最小二乗法を解く
さて、何をやっているかがわかったら、めんどくさい計算はエクセルに任せてしまいましょう。エクセルにはこの問題を解いて直線の式を計算してくれる「linest関数」があります。今回は、先ほどの項目で出てきた直線を「y=ax+b」としてその「a」と「b」を求めてみましょう。
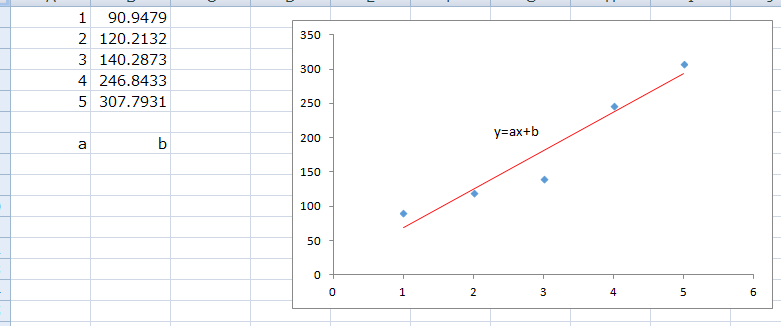
上の図を見てください。先ほどの数値の並びの散布図と、その元データが並んでいます。この散布図の中にある、「y=ax+b」の式にあてはまるaとbを求めます。
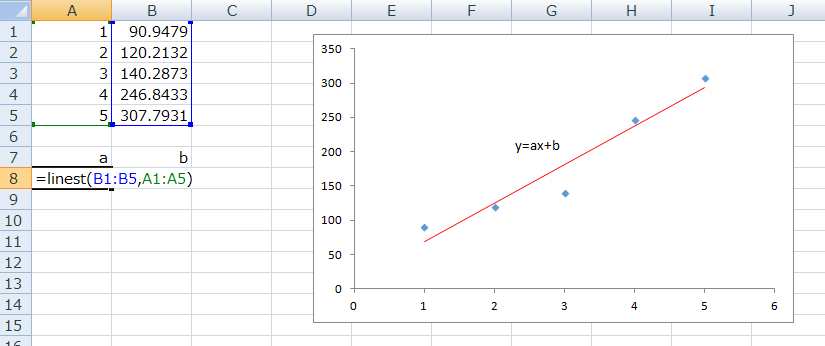
求めるaを表示したいセルに上図のように
＝LINEST(B1:B5,A1:A5)
と入力してエンターを押してください。
Microsoft365の場合
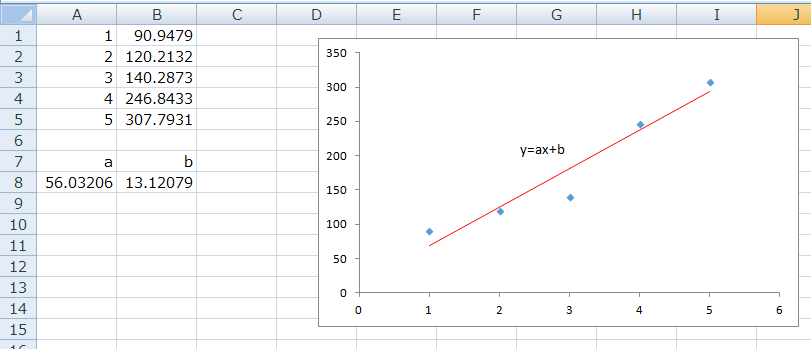
図のようにaの値が表示され、自動的にその右隣にbの値が表示されます。
Microsoft365以前のエクセルの場合
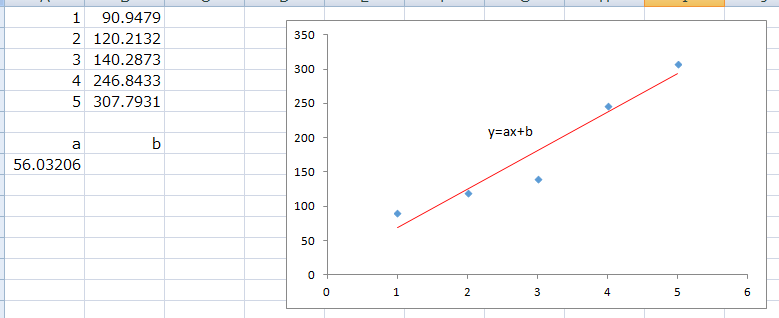
図のようにaの値のみ表示されます。そのため、bに同様に式を入れて求める必要があります。
aと同じように式を利用する
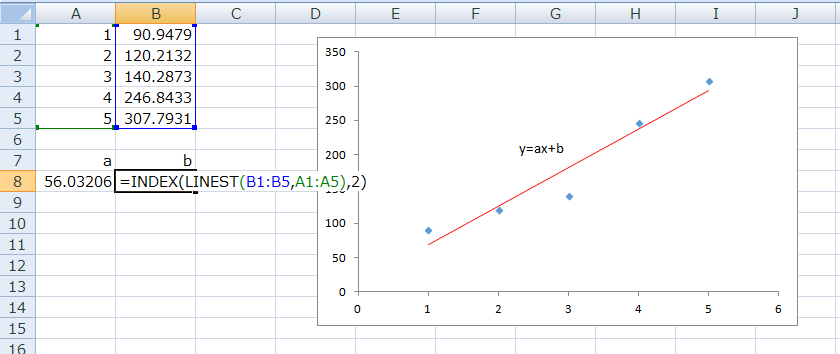
aと同じように式を利用するやり方として、以下の式を使います。
＝INDEX(LINEST(B1:B5,A1:A5),2)
aを求めるときに使用した式を「INDEX( ,2）」で囲んでいるだけです。なぜこんなことをしているかは後ほど説明します。
aと同時に求める
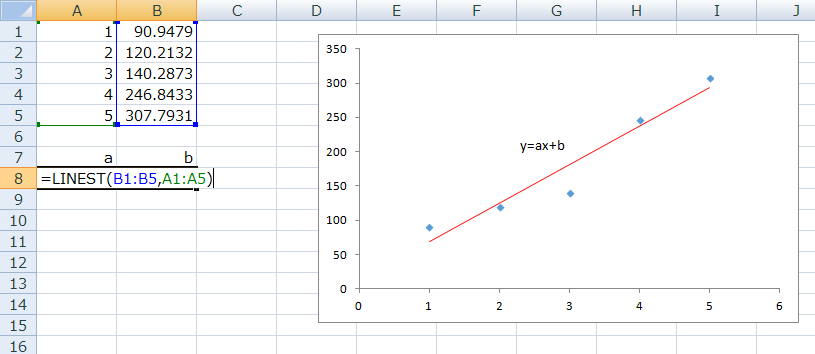
最初にaを求めるときにaを表示するセルのみを選択して式を入力しましたが、aを求めるセルとbを求めるセルを同時に選択して、aのセルに同じ式を入れます。そして式を入れ終わったら、エンターの代わりに「ctrl」と「shift」を押しながらエンターキーを押します。
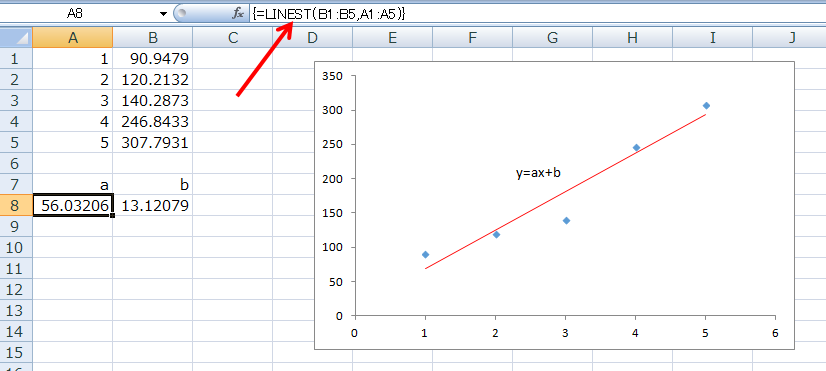
すると、上の図のように式の部分に「{ }」がついた状態で式が表示され、aとbがそれぞれのセルに表示されました。
【補足】なんでこんな求め方をするの？
linest関数を使用すると、表示させているセルには一つの数値しか表示されませんが、関数は{「傾きa」, 「切片b」}２つのデータを持った、配列という形でデータを持っています。これは後ほど説明しますが、変数が多くなれば{「傾きa」, 「傾きb」, 「傾きc」, 「切片d」}と、多くのデータを持った配列が返ってきます。
そのため、「〇番目のデータ」であることを指示するために「index( ,〇)」を追加してやる必要があります。この指示がないと１番目のデータが表示されることになります。
２つ目の求め方「aと同時にbを出す方法」も同様で、配列を一気に表示してやるのが「aと同時にbを出す方法」の表示方法です。
実際に分析するときの注意点
簡単な問題をlinest関数を使用して最小二乗法で解くやり方を見てきましたが、実際に解析を行うときには少し注意が必要です。
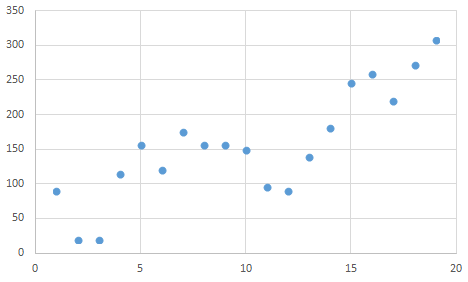
例えば上の図を見てください。先ほど解いたのと同じような点の配置なので、これも同じようにlinestを使用してy=ax+bに当てはめればよいのではないか、と思うかもしれません。
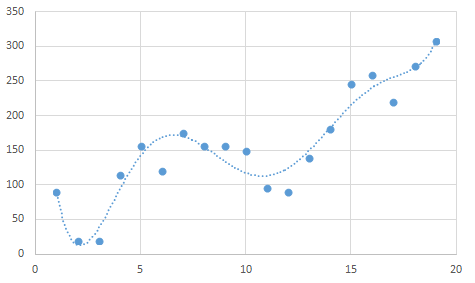
しかし、実は下図のようにｘの6次式に誤差を加えたもので、y=ax+bで解くとすこし数値がずれてきます。重要なことは、そのデータがどのようなデータで、この式に当てはめてよいかを考えてみることです。これは統計の知識ではなく、それぞれのデータに関する知識になります。
特に、今回は変数が一つだけ、いわゆる単回帰分析と呼ばれるものを考えていますが、世の中には変数が一つだけでは決まらないことも多く存在するため、データを見ることは非常に重要です。
一方、数値の関係性がわからないため、とりあえず散布図にしてみたらy=ax+bと表せそうなのでまずは傾向をつかむためにこの方法をやってみた、という場合もあるかもしれません。この場合もどの程度の精度で見ているのかを考えながら解析をすることが重要になります。
- このデータはこの式で表してよいかを考える
- 出てきた結果がイメージと大きく違うことはないかを考える
- どの程度の確からしさを求めて解析しているかを考える
もっと簡単な方法で分析してみる
近似曲線を使用する
もっと、非常に簡単に最小二乗法をする方法を考えてみます。
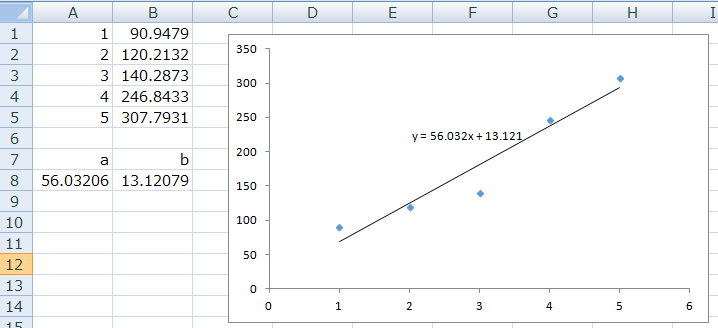
先ほどlinest関数で傾きと切片を出したグラフに、「グラフの要素を追加」＞「近似曲線」＞「線形」を選択します。すると、先ほど一番最初に考えた「y=ax+b」のグラフが散布図に追加されます。
さらに、「グラフの要素を追加」＞「近似曲線」＞「そのほかの近似曲線オプション」を選択し、「グラフに数式を表示する」を選択します。
すると先ほどlinest関数で求めた式がグラフの横に表示されました。これで簡単に式を求めることができます。
いろいろな近似曲線
先ほど「グラフの要素を追加」＞「近似曲線」＞「そのほかの近似曲線オプション」＞「近似曲線のオプション」の中に「多項式近似」がありました。これを利用すると二次式以上の近似曲線を描画することが可能です。
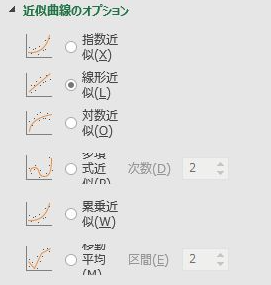
「実際に分析する際の注意点」の項目で出てきた点群を、まずは線形近似してみます。
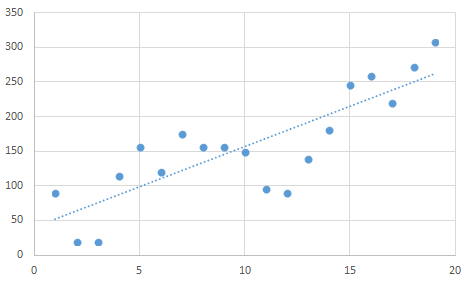
次に、「近似曲線のオプション」から「多項式近似」を選択し、次数を「３」としたものがこちら。
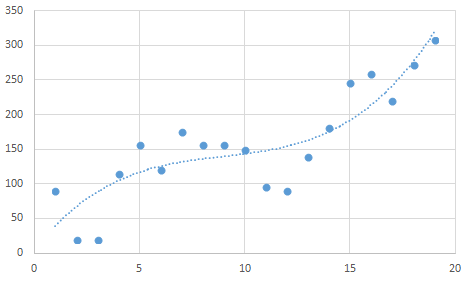
次に次数を「６」としたものがこちらです。あてはまりがよくなってきました。
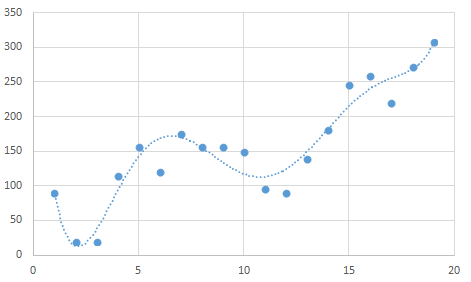
結局どの曲線が正解なの？
先ほども説明した通り、この点群は６次の式から作られていますが、実際の点群を式に当てはめるときは次数とあてはまりの良さのバランスを見ることも重要です。
次数をひたすら上げ、くねくねと曲がったグラフを作ればすべての点を通過するグラフは作成可能かもしれませんが、各点は「実際の値＋誤差」から成り立っていますので、誤差も含めて完全にあてはまる式がこの点群の実際を表しているとは限りません。この点群にだけ過剰にあてはまってほかの点を抜き出してみたらあたらないこの状態をオーバーフィッティングといいます。
極力次数が低く、かつあてはまりの良いものが一番好ましいのですが、先ほどもあったように元のデータを理解することがこのあたりの問題を解決する一番の方法です。
なお、元のデータを理解したうえでも次数とあてはまりのバランスに迷うときは「赤池情報量基準（AIC）」という考え方もあるので、興味のある方は参考にしてみてください。
単回帰分析だけじゃないlinset関数
単回帰分析とは？
単回帰分析とは、先ほどのy=ax+bの式で、yを求めるために考えたxが一つの場合をいいます。今回の場合だと、重さyは長さxで決まるので単回帰分析でした。
それに対し、xが二つ以上出てくるものを重回帰分析といいます。今回は、例としてアイスの売り上げyを、「気温」「湿度」「売っている場所の地価」から求める場合を考えてみます。
重回帰分析でもlinset関数を使ってみる
この場合、yを求める式は「y=ax1+bx2+cx3+d」となります。
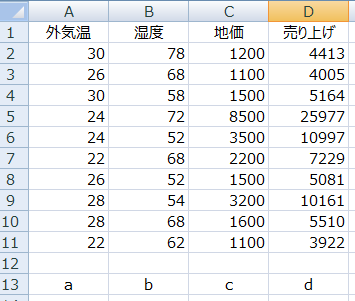
エクセルは、単回帰分析の時と同じようにx1、x2、x3にあたるデータ。そしてyを上図のように順に並べます。なお、このデータは説明用に作成したので参考データです。
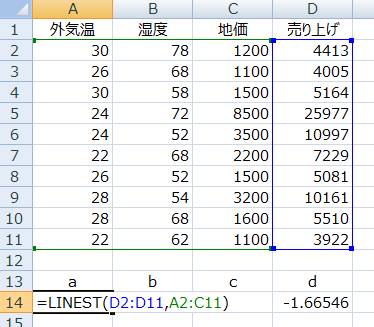
基本的な考えは単回帰分析の時と同じで、最初にyの部分、次にxの部分を入力します。今回はxが複数行にまたがっているので、まとめて囲んで入力します。
=LINEST(D2:D11,A2:C11)
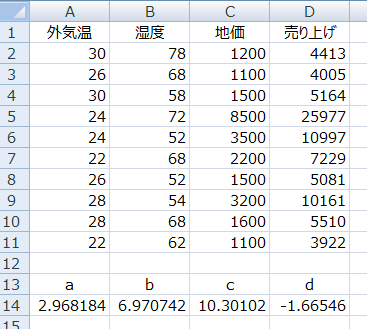
するとaからdの値が下図のように表示されました。
エクセルでの重回帰分析についてこちらでも詳しく解説しています！
まとめ
今回はエクセルで最小二乗法を使用して単回帰分析・重回帰分析を行うために、linest関数を中心に解説しました。関数の使い方としてはそんなに難しくないと思いますが、説明の中にあるように極力データを理解して正しい使い方をしていただけたらと思います。
