エクセルで標準誤差を出す必要に迫られたことはありませんか？
「標準誤差はエクセルでどのように表示すればいいの？」
「標準誤差をグラフに表示するにはどうしたらいいの？」
今回はそのような疑問をお持ちの方のために、標準誤差の出し方とそのポイントをわかりやすく解説します。
標準誤差を用いるポイント
特に工業製品などのデータをまとめる際、必ず付きまとってくるものに誤差・ばらつきがあります。統計的にデータを取りまとめた結果に標準誤差が記入されているかどうかで統計的に管理している説得力が増します。
特にグラフで標準誤差を記入しておくと、管理値、もしくは規格値との関連が一目でわかり非常に便利ですし、資料の信頼性が増します。「これはうまくいったときのデータでよね？」とか、「ばらついたら不良が出るんじゃないの？」といったコメントは耳にしたことがあると思います。
ばらつきというと標準偏差がよく注目されますが、今回は実際の測定データしかなくて、全体がどの程度ばらついているかわからない場合に使用される標準誤差の求め方と表示の仕方について解説していきます。
実際にエクセルで表をまとめる際には、「データ全体は不明だが、今ここにはこのデータしかない」といった状況でデータをまとめることも多いと思いますので、この標準誤差の出し方、表示のしかたを覚えてぜひ活用してください。
エクセルで標準誤差を求める方法
式（関数）で求める
標準誤差に関する細かい説明は後回しにして、まずはエクセルで標準誤差を求める方法を確認していきます。
標準誤差（SE）は以下の式で表すことができます。
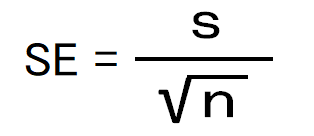
式の意味などは後程説明します。まずはエクセルで求めることを考えてみます。ここで
- SE・・・標準誤差（Standard Error）
- s・・・標準偏差
- n・・・サンプル数
となります。データが入っているセルがA１～A７の場合、これをエクセルの関数に当てはめると、
STDEV.S(A1:A7)/SQRT(COUNT(A1:A7))
となります。なお、STDEV.Sはエクセル2010以前はSTDEVという名前でした。2010以前のバージョンで作成する場合は「STDEV.S」の部分を「STDEV」に置き換えてください。
実際にエクセルのデータから標準誤差を算出するときは、特定のセルに結果を表示させたい場合が多いと思いますのでこのような式を書くことが多いと思いますが、結果があっているか確かめたい場合や関数を忘れてしまったが取り急ぎ標準誤差の結果のみ確認したい場合のために基本統計量を表示する方法も確認しておきます。
基本統計量を表示する
事前準備
エクセルの機能、分析ツールを使用します。ただし、エクセルの初期状態ではこの機能は表示されないため、以下の手順で表示します。
「オプション」から「アドイン」を選択、「分析ツール」にチェックを入れます。これをしないと次の項目で使用する「分析ツール」アイコンが表示されません。
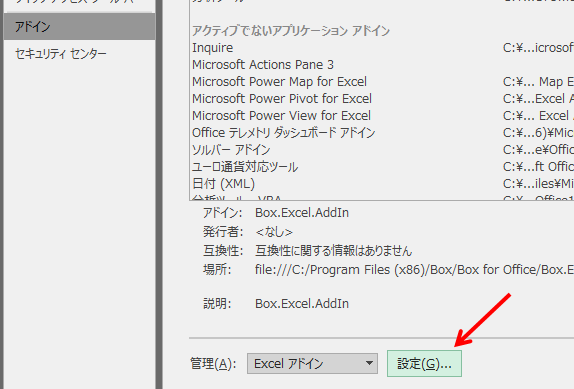
基本統計量の表示
メニューの「データ」＞「分析」＞「データ分析」を選択します。アイコンが表示されていない場合は<事前準備>の項目を確認してください。
「分析ツール」の中から「基本統計量」を選択してください。
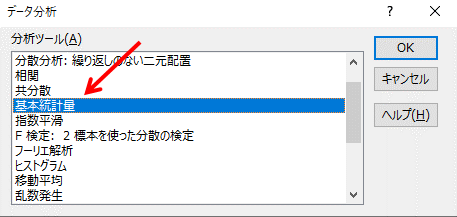
「入力範囲」にデータの範囲「A1:A7」を。「出力先」にデータを出力したいセルを入力し、「統計情報」のチェックを入れて「OK」を押します。
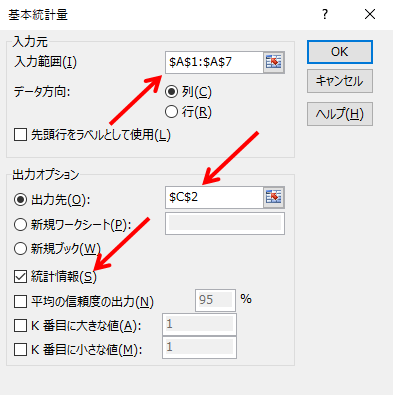
すると、上から２番目に「標準誤差」が表示されます。式で標準誤差を算出した場合は、一度この統計情報を表示させ、結果があっているか確認するのがよいと思います。
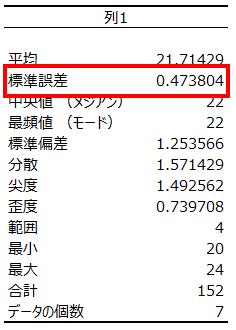
エクセルのグラフに表示する方法
先ほどの式による算出と同じように、データがA1～A7に入っている状態でグラフを作成します。まずはA1～A７を選択した状態で「挿入」＞「グラフ」を選択し、棒グラフを作成します。
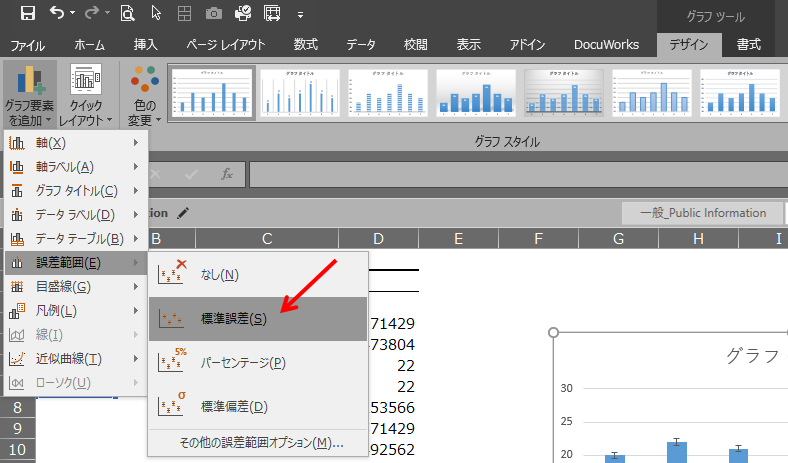
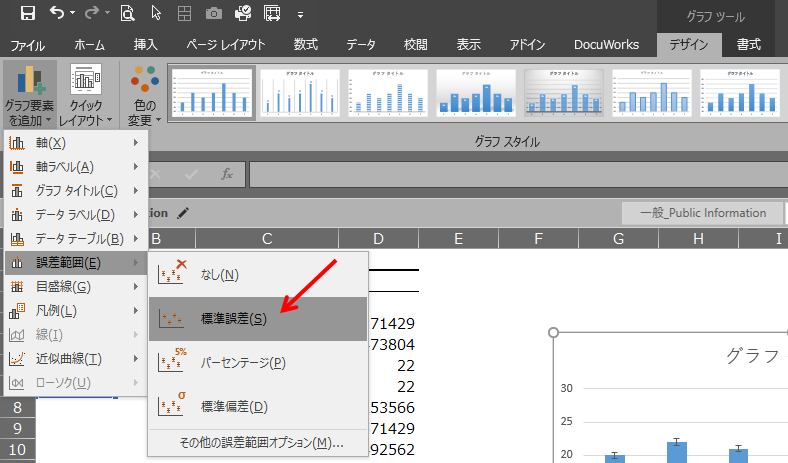
棒グラフを選択した状態で、「グラフツール」＞「デザイン」＞「グラフ要素を追加」＞「誤差範囲」＞「標準誤差」と選択していきます。
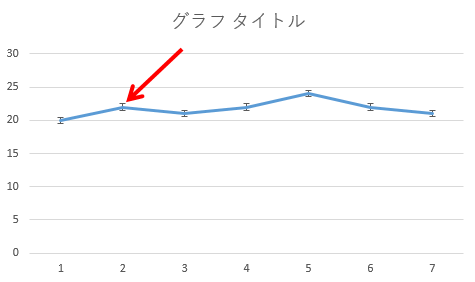
グラフに標準誤差の範囲を示す表示が現れました。
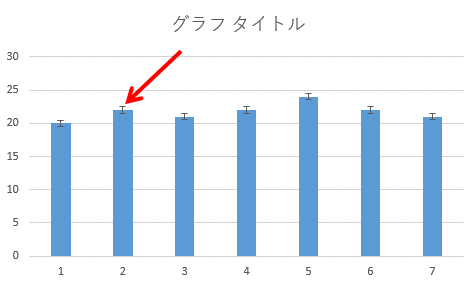
折れ線グラフでも同様の操作で標準誤差を表示できます。
そもそも標準誤差ってなに？
さて、ここでいままで式やエクセルの機能に従って標準誤差を求めてきましたが、そもそも標準誤差って何でしょう？あまり統計的なことを考えずに、統計的な言葉を使わずに、どのようなことをしているか考えてみましょう。統計的な考え方は次の項目で考えてみます。
冒頭でも出てきましたが、標準偏差が「データ全体の偏り具合」を示すのに対し、標準誤差は今ここにあるデータが本来の全体のデータに対してどの程度誤差があるか、を示しています。
今手元にあるデータ
統計では、今手元にあるデータは標本といって、これはすべてのデータである母集団のなかから取り出した一部である、と考えます。
たとえば、ある機械で作られた製品Aを考えてみます。今日、この機械Aで作られた製品を母集団とすると、その母集団には重さがあり、その重さにはばらつきがあります。この母集団の平均を母平均、ばらつきを標準偏差といいます。
その母集団のなかからサンプルとして７つのデータを取り出すとします。そのサンプルを標本と言って、その平均を標本平均、その標本平均が母平均からどの程度ばらつくかを標準誤差といいます。
標準誤差の式
一番最初に出てきましたが、標準誤差の式は
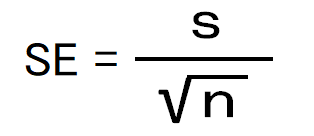
で求められました。大きく２つのパターンを考えてみるとイメージがわくと思います。
ばらつきが大きい場合
ばらつきが大きい場合、これは分子のｓ（標準偏差）がとっても大きい場合ですが、ｓを大きくすると標準誤差も大きくなります。もともとのデータのばらつきが大きければ、データを取り出したときの平均の誤差が大きくなることは容易にイメージがつきますよね。
大きくばらつくデータからデータを標本として取り出したときの、標本平均のばらつきはもちろん大きくなるわけです。
データ数が小さい場合
標本数（＝ｎ）が１の場合、ＳＥ（標準誤差）はｓ（標準偏差）と同じ値になります。「標本平均＝標本データ自体」のばらつきは、母集団からデータを一つ取り出したわけですから標準偏差になります。これもイメージ通りではないかと思います。
データ数が大きい場合
今度は標本数ｎが大きい場合を考えてみます。ｎがどんどん大きくなっていくと、ＳＥの値はどんどん小さく、最終的には0に近づいていきます。イメージ通りだと思いますが、データを取り出したときに、取り出す数が少ないとばらつきは大きくなりますし、たくさん取り出すと、最終的にばらつきが収束して０に近づいていきます。これは大数の法則と呼ばれています。これもイメージ通りですね。
少し統計的に標準誤差を考えてみる
標準誤差の式は、ｔ分布と同じ考えになりますが、平均μ、標準偏差σの正規分布の確率密度分布である母集団から取り出したサンプルの平均値が作る、確率密度分布の標準偏差と同じ値をとります。もちろん、この場合の平均値は母平均と同じになります。
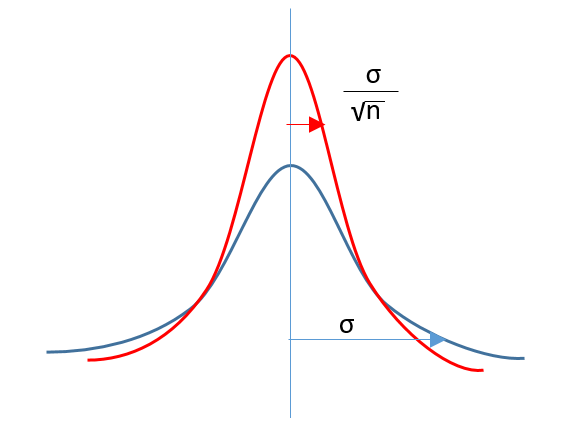
これを上図のようにサンプルｎの平均値のグラフで考えると、
・n=1の時、元データからサンプルを一つ取り出すのと同じなので標準誤差は元のデータの標準偏差と同じになります。
・n＝∞の時、標準誤差は０に近づいていきます。そのため、抜き出したサンプルの平均値自体が大数の法則に従って母集団に近づいていくことがわかります。
またnが非常に大きい時、標準誤差が０に近づき標本平均が母平均に近い値になるため、正規分布に近づくことは中心極限定理に等しくイメージしやすいと思います。
まとめ
今回はエクセルによる標準誤差の求め方と、簡単ですが標準誤差について解説しました。工業製品などのばらつきのあるデータについては、ばらつきの考えが非常に重要になりますし、誤差を表示しておくことでちゃんとばらつきについて考えていることがわかり、データの説得力が増します。
本文にあるように簡単に設定できますので、ぜひ活用してください。
