第12章では、分散分析について解説していきます！
第9章及び第10章で、2つまでの母集団の母平均の差を考える際には、t検定かz検定を使う事を学んできました。
しかし、3つの母集団の平均の差を考える機会も多くあります。
この時に用いるのが分散分析です。
非常に使い勝手の良い仮説検定になっているので、是非マスターしていって下さい！
また、本章で用いるExcelファイルは以下からダウンロードして下さい！
本連載講座【Excelによる統計解析講座】では、Excel未経験の方、自身の無い方でも順を追って学習でき、基礎からデータ分析に必要なスキルまでを身に付ける事が出来ます。
画像が多く、ビジュアルで理解しやすくなっておりますので、読み物が得意ではないという方も大丈夫です！
また、第７章からは、統計学の分野も扱う為、様々な方に役立つ講座となっております。
そのため、
- Excelを仕事で使う可能性のある方
- Excelに自信のない方
- データ分析をExcelでやりたい方
等は是非、TechTeacherが運営する【Excelによる統計解析講座】を使って学習していって下さい！
〈目次〉
第1章：【テーブル】Excelのテーブル（フィルター）を解説！
第2章：【SUM,AVERAGE】Excelの基本的な関数を解説！
第3章：【XLOOKUP,COUNTIF】データ分析の為のExcel関数を解説！
第4章：【棒,折れ線,散布図】Excelの基本的なグラフを解説！
第5章：【ピボットテーブル】Excelの便利機能”ピボットテーブル”を紹介！
第6章：【プレゼン資料】Excelグラフの体裁の整え方について解説！
第7章：【相関分析】相関係数と共分散をExcelを用いて解説！
第8章：【確率変数・正規分布】確率変数や正規分布をExcelで解説！
第9章：【t検定・z検定】母平均と母分散の仮説検定について解説！
第10章：【t検定・z検定】2つの集団の母平均・母比率の仮説検定を解説！
第11章：【仮説検定】カイ二乗検定とF検定をExcelで一瞬で解く！
本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。
分散分析とは
分散分析とは
複数のデータの母平均を比較する際、ただ平均を比べるのでは、偶然その平均になった場合を考慮出来ません。
そこで、データのばらつきを考慮する事で、平均の差が誤差の範囲内にあるかを考える必要があります。
そこで用いられるのが分散分析です。
この分散分析では、データのばらつきを考慮した上で、その平均の差が本当に有意であるかを数値的に判断する事が出来ます。
その為、この分散分析を用いる事で、どんな要因が結果に大きく影響しているかについて分析する事が出来ます。
この分散分析は、分析するデータの形から、一元配置と二元配置というものに分ける事が出来ます。
一元配置とは
データ分析において、実験的に変化させる要因を因子、因子を質的・量的に変える条件を水準と言います。
この時、1つの因子についてのみ取り上げて、複数の水準の結果との関係を分析する手法を一元配置と言います。
例えば、ある屋台の「天気」という因子について、「晴れ」、「曇り」、「雨」という水準を設けて、その売り上げについて一元配置を行います。
この時、各水準間に有意な差があると判断できれば、天気が売り上げに関係していると判断する事が出来ます。
二元配置とは
次に、2つの因子について、各水準と結果との関係を分析する手法を二元配置と言います。
この二元配置は、更に交互作用の有無によって、繰り返しありと繰り返しなしに分けられます。
交互作用とは、1つの因子の水準の関係が別の因子の水準に影響される事を言います。
例えば、ある屋台に関して、「クレープ」を売った日の売り上げは、「雨」の日よりも「晴れ」の日の方が売り上げが大きいとします。
しかし、「チュロス」を売った日には、「雨」の日の方が「晴れ」の日よりも売り上げが大きいとします。
この時、「クレープ」の条件下では「雨」<「晴れ」であったのに対し、「チュロス」の条件下では「雨」>「晴れ」となり、
「天気」という因子に、「食べ物」という因子の水準が影響して売り上げが変化しています。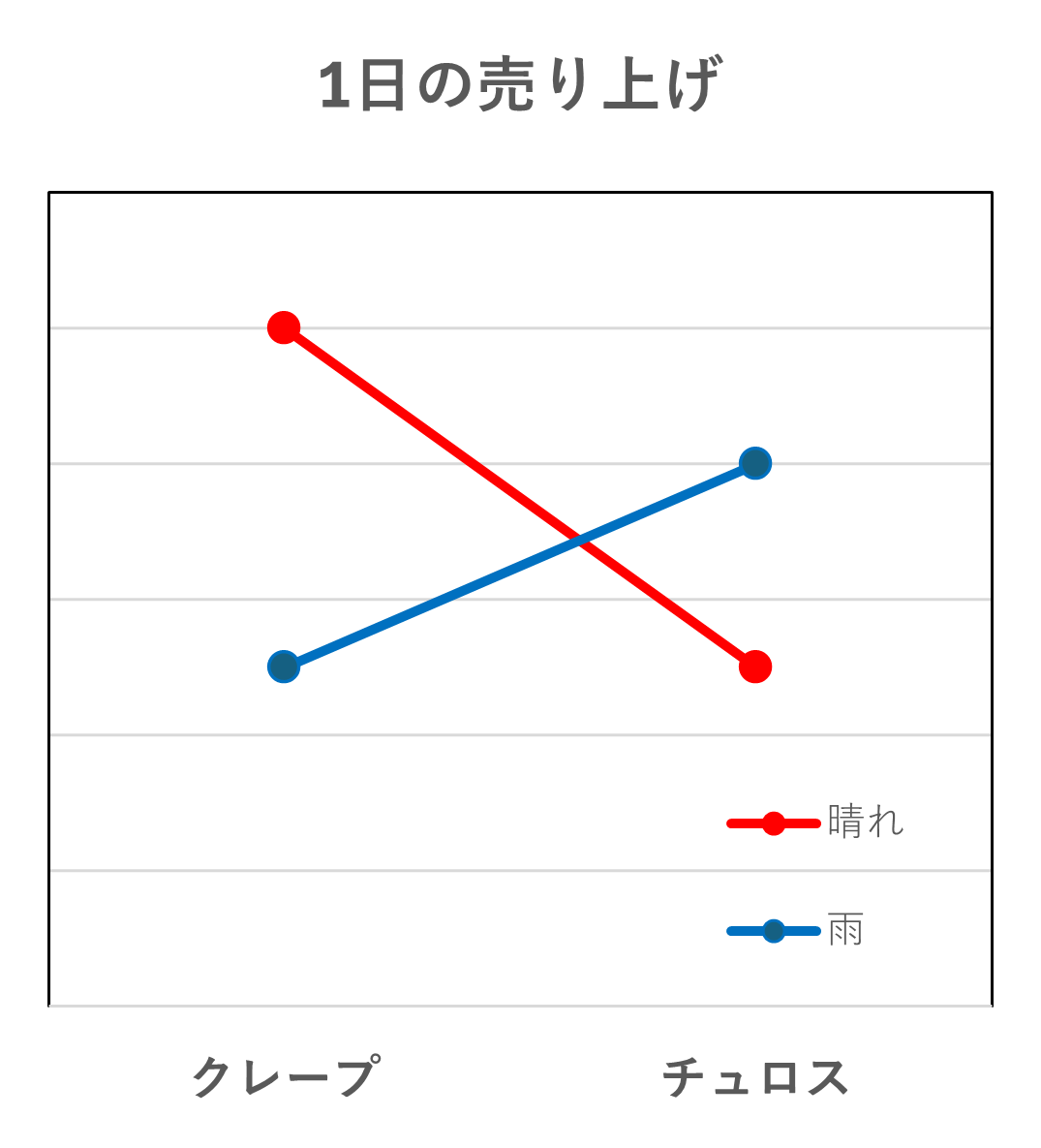
このような作用を交互作用と言います。
交互作用が予想される、「天気」と「食べ物」の様なデータに関して、「晴れ」の時の「クレープ」の売り上げと「雨」の日の「チュロス」の売り上げが1日分ずつしかないと、偶然売り上げが逆転した可能性を捨てられません。
その為、交互作用があると予想されるデータには、各因子の組み合わせに対して複数のデータを用意する、繰り返しありの二元配置が用いられます。
これに対し、交互作用ないと予想されるデータでは、互いの因子を無視できる為、各因子について、複数のデータがあるとみなせて、繰り返しなしの二元配置が用いられます。
最後に、ゲームセンターのゲーム機の種類と景品における1週間の売り上げに関して、
一元配置と繰り返しありとなしの二元配置を適用するデータの例を挙げておきます。
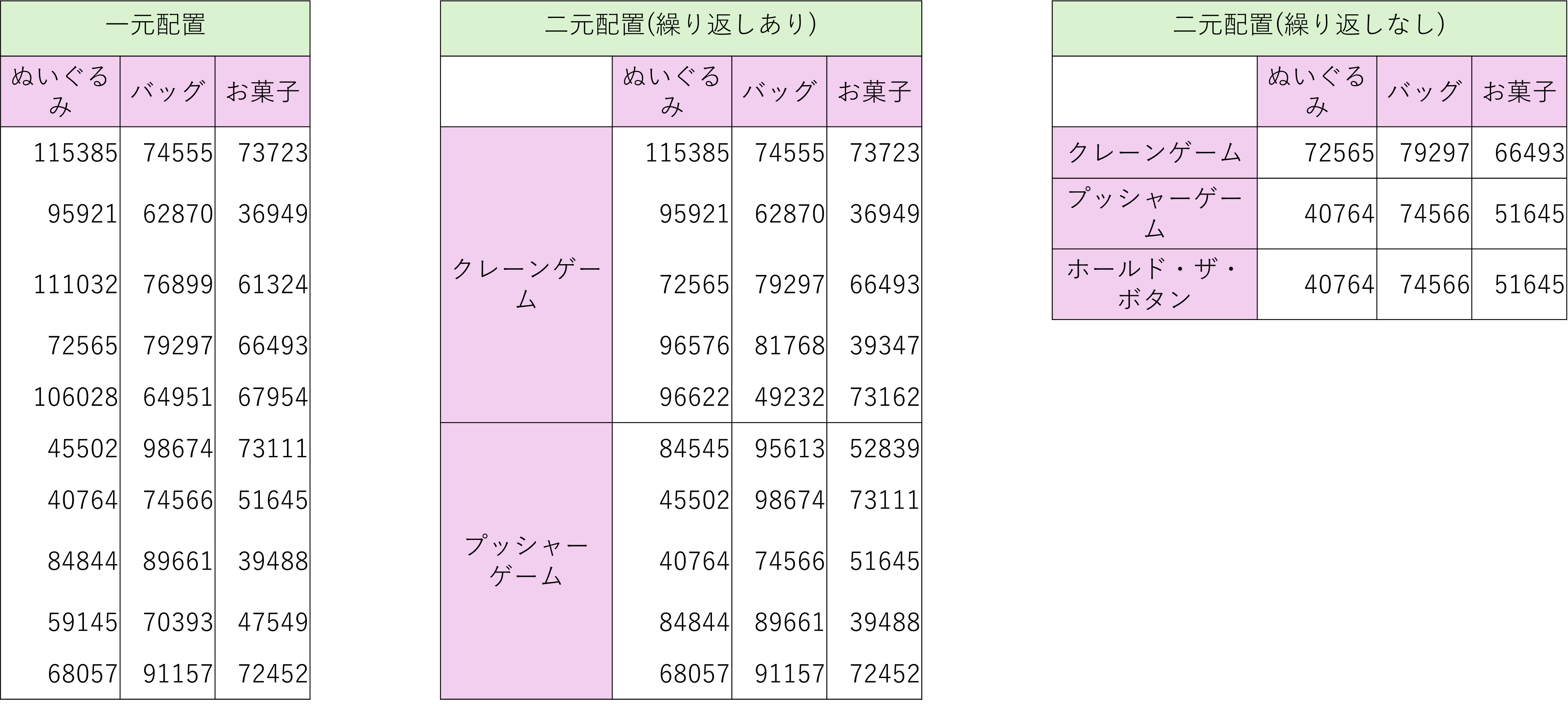
分散分析表
概形
分散分析表の概形は一元配置、二元配置(繰り返しあり)、二元配置(繰り返しなし)によって多少異なります。
ここでは例として、一元配置の分散分析表の例を挙げます。
これまで、Excelで統計学を勉強してきた皆さんなら、自由度、分散については、分かると思います。
その為、以下では、変動(平方和)、観測された分散比及びF境界値、P値について解説していきます。
変動(平方和)
まず、変動(平方和)について解説していきます。
この変動は、「グループ間」、「グループ内」、「合計」でその計算方法が少し異なります。
因子Aの水準を\(A_{1},A_{2},A_{3}\)とし、全体のデータ数をnとします。
まず、「グループ間」の変動に関して、水準\(A_{1}\)のデータを全て\(\bar{A_{1}}\)に変え、水準\(A_{2}\)、\(A_{3}\)に関しても同様に行います。
ここで、全てのデータについて、
\[ \sum x^{2} – \frac{(\sum x)^{2}}{n} \]
を計算した値が、「グループ間」の変動(平方和)となります。
次に、「グループ内」の変動に関して、水準\(A_{1}\)のデータを全て\(A_{1}-\bar{A_{1}}\)に変え、水準\(A_{2}\)、\(A_{3}\)に関しても同様に行います。
ここで同様に、全てのデータについて、
\[ \sum x^{2} – \frac{(\sum x)^{2}}{n} \]
を計算した値が、「グループ内」の変動(平方和)となります。
最後に、元データに関して、
\[ \sum x^{2} – \frac{(\sum x)^{2}}{n} \]
を計算した値が、「合計」の変動(平方和)となり、これを偏差平方和と言います。
これらの算出方法に関しては、自身で分散分析表を算出する際に参考にしていただければと思います。
F値
次に、F値について解説していきます。
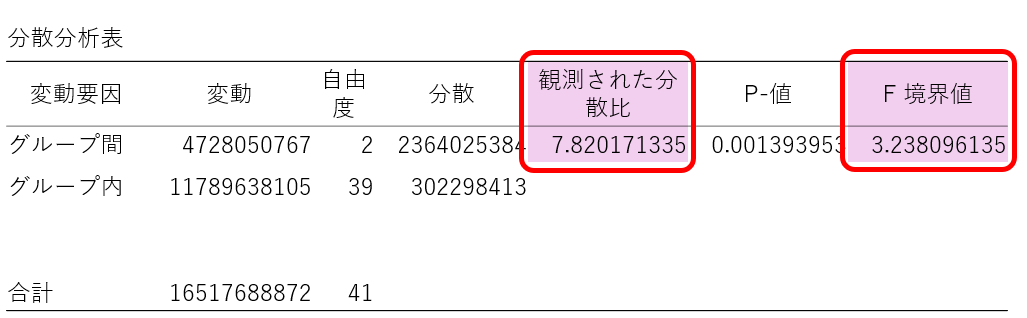
F値とは、簡単に言うと、これまでの仮説検定で言う所のT値です。
分散分析では、母分散を比較する事でその差が有意であるかを判断するため、この分布はF分布に従い、F検定を用いています。
このF検定について、詳しく知りたい方は、前章の第11章：【仮説検定】カイ二乗検定とF検定をExcelで一瞬で解く！を読んでみて下さい！
この時、「観測された分散比(=F値)」は「T値」、「F境界値」は「棄却限界値」になり、観測された分散比>棄却限界値となる時に、グループ間の母平均には差があるという事が出来ます。
p値
そして、最も重要なのがp値です。
今回は、このp値のみを用いて母平均の差が有意であるかを判断していきます。
このp値はここでは、「母平均の差が有意でない確率はどのくらいか」を表していて、この値が有意水準を下回れば、その項目において、母平均の差があると判断する事が出来ます。
通常、有意水準には5%が使われるため、「p値が0.05を下回れば母平均には差があると判断できる」と覚えて下さい！
実際に分散分析をしてみよう！
では早速、分散分析を行っていきましょう！
分散分析表を自作する事も出来ますが、Excelには「データ分析」ツールという便利なツールがあるため、これを使って分散分析を行っていきましょう！
このデータ分析ツールが分からない方は、第7章：【相関分析】相関係数と共分散をExcelを用いて解説！内の「共分散と相関係数のデータ分析ツールを用いた算出方法」から、データ分析ツールを設定してみて下さい！
一元配置
例題1（一元配置）
あるゲーム機製造メーカーが、自社の提供するクレーンゲーム機等の売り上げを上げたいと考えています。そこで、景品の種類による1週間の売り上げを比較することにしました。
Excelファイル1ページ目のデータを用いて、各景品の種類の母平均に有意な差があるか(=景品の種類が売上に関わる要因になり得るか)を有意水準5%で分散分析してみましょう！
今回は、1つの因子について分散分析を行っていくため、一元配置を使ってデータ分析をしていきます。
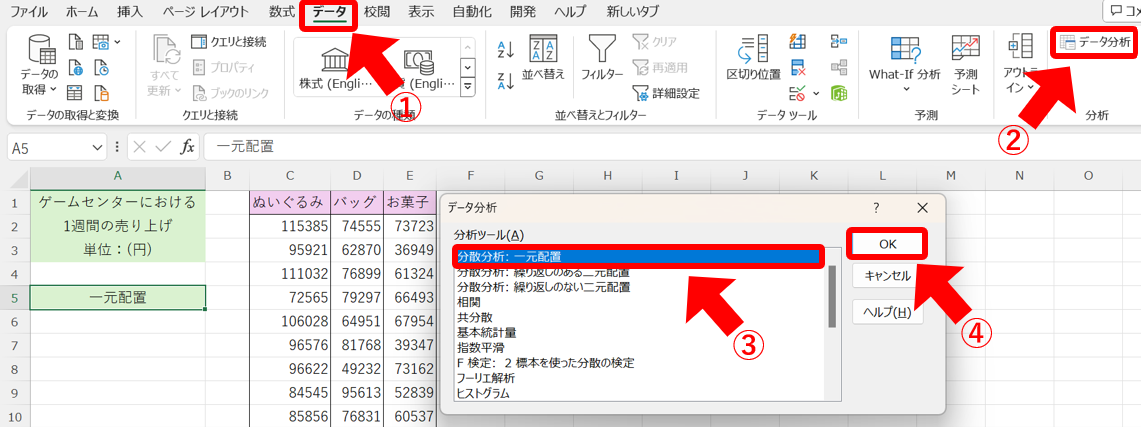
まず、①「データ」タブから、②「データ分析」ツールを開きます。
次に、③「分散分析：一元配置」を選択して、④「OK」を押します。
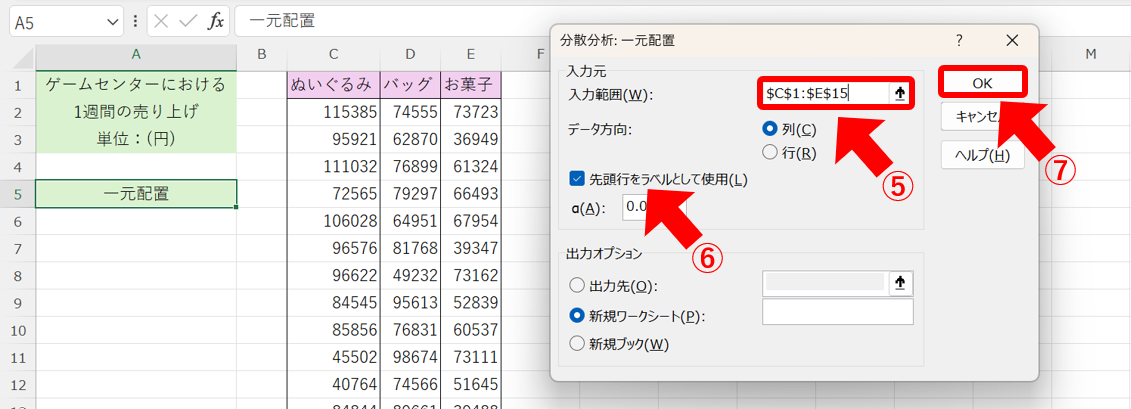
続いて、⑤データ範囲を選択して、⑥景品の種類が含まれているので、「先頭行をラベルとして使用」にチェックを入れ、最後に⑦「OK」を押します。
すると、別のページに以下の様に分散分析表等のデータが表示されます。
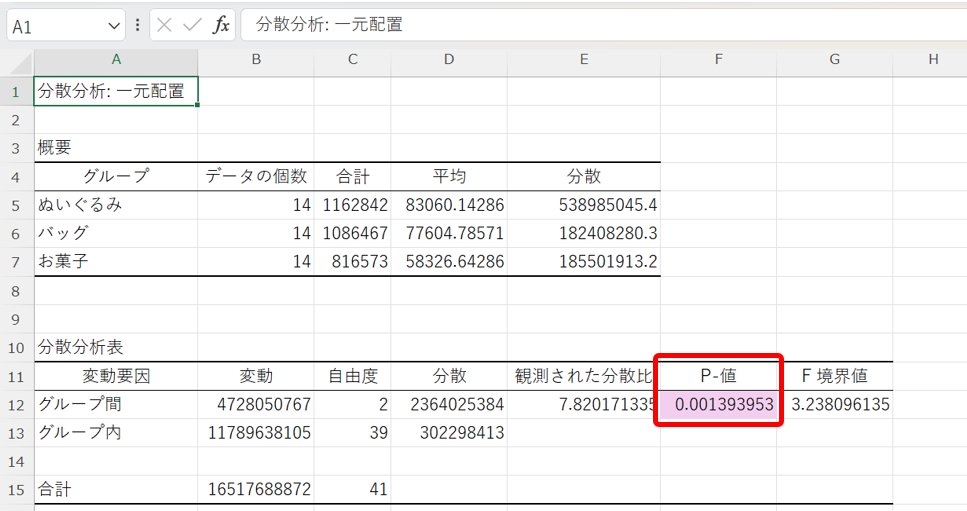
この分散分析表について、前述した様に、p値だけを見ます。
この時、有意水準5%より、p値<0.05であるから、景品の種類間の母平均の差は有意であり、景品の種類が売り上げに関係していると判断できます。
二元配置(繰り返しあり)
例題2（繰り返しありの二元配置）
あるゲーム機製造メーカーが、自社の提供するクレーンゲーム機等の売り上げを上げたいと考えています。そこで、景品の種類及び、クレーンゲームの種類による1週間の売り上げを比較することにしました。
Excelファイル2ページ目のデータを用いて、各景品の種類の母平均に有意な差があるか(=景品の種類が売上に関わる要因になり得るか)を分散分析してみましょう！
ただし、景品の種類とクレーンゲームの種類の間の交互作用はあると予想します。
この問題では、「景品の種類」と「クレーンゲームの種類」という、2つの因子に関して、交互作用があると予想されている為、繰り返しありの二元配置を使って分散分析していきます。
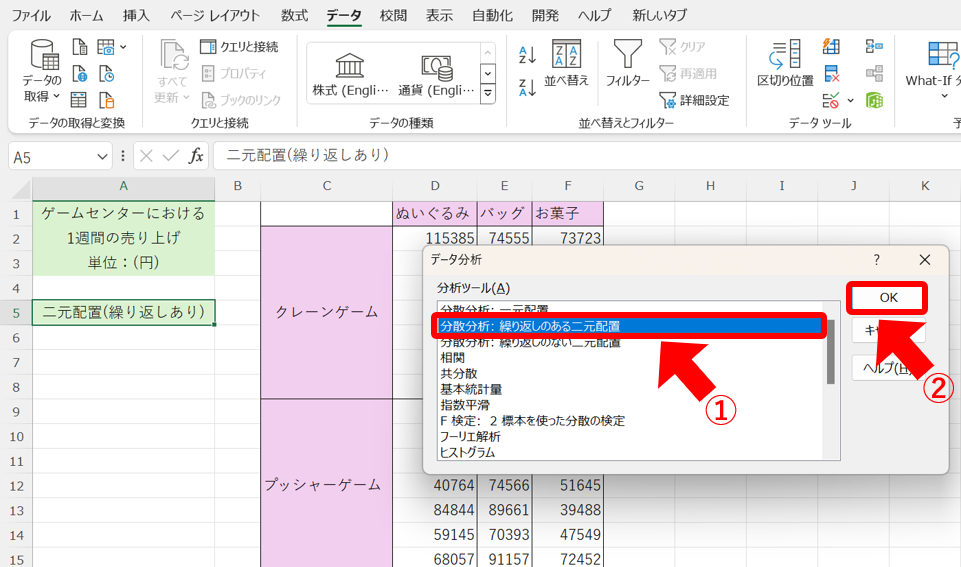
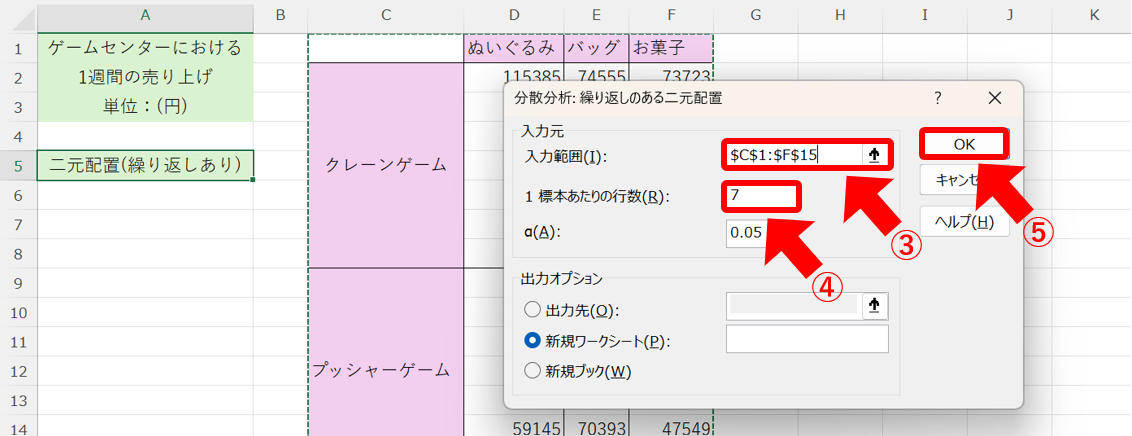
まず、先ほどと同様に「データ」タブから「データ分析」ツールを開いて、①「分散分析：繰り返しのある二元配置」を選択して、②「OK」をクリックします。
次に、③データ範囲を選択して、④「1標本あたりの行数」に1つ行の項目に入っているデータ数を入力します。ここでは、「クレーンゲーム」と「プッシャーゲーム」に7個ずつデータがあるため、7を入力します。
最後に、⑤「OK」をクリックします。
すると、別のページに以下の様に分散分析表等のデータが表示されます。
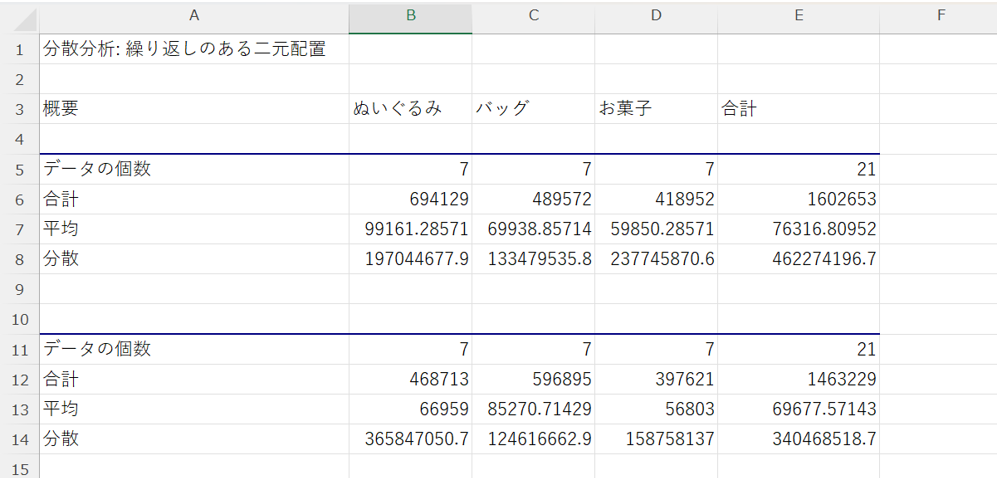
下にスクロールして、分散分析表のp値を確認すると、以下の様に3つのp値が確認できます。
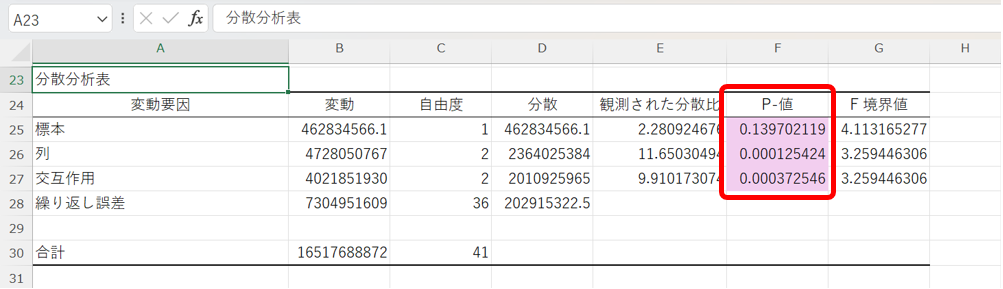
このp値に関して、標本が「クレーンゲームの種類」間の母平均の差、列が「景品の種類」間の母平均の差、交互作用が2つの因子を組み合わせて考えたときの母平均の差になります。
これより、列と交互作用のp値が0.05を下回っているので、この2つの母平均の差が有意であり、
「景品の種類」と「景品とクレーンゲームの種類の組み合わせ」が売り上げに影響している事が判断できます。
最後に、この様に分散分析を行う際には、その結果が大きくなる条件を明確にするために良く折れ線グラフが用いられます。
下図の様に、データ分析の結果から、平均のデータの抜き出して表にします。
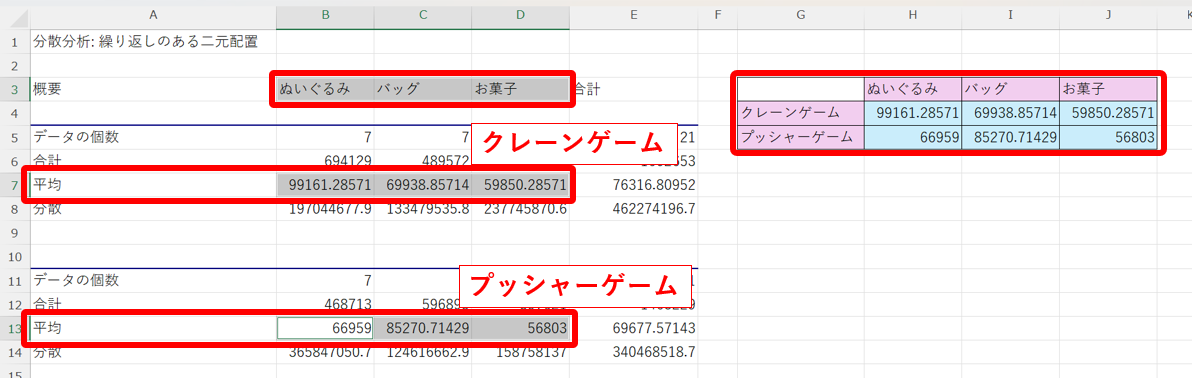
次に、その表から、「マーカー付き折れ線」のグラフを作ります。
最後に、どの因子の水準同士の売り上げが最も大きくなるかについて調べます。
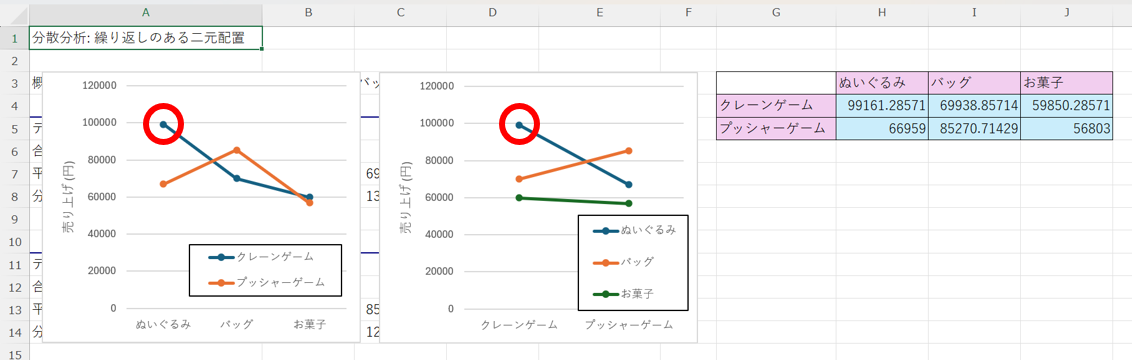
上の図より、今回は「ぬいぐるみ」の「クレーンゲーム」の売り上げが最も大きくなっている事が分かります。
二元配置(繰り返しなし)
例題1（繰り返しなしの二元配置）
あるゲーム機製造メーカーが、自社の提供するクレーンゲーム機等の売り上げを上げたいと考えています。そこで、景品の種類及び、クレーンゲームの種類による1週間の売り上げを比較することにしました。
Excelファイル3ページ目のデータを用いて、各景品の種類の母平均に有意な差があるか(=景品の種類が売上に関わる要因になり得るか)を分散分析してみましょう！
ただし、景品の種類とクレーンゲームの種類の間の交互作用はないと予想します。
この問題では、「景品の種類」と「クレーンゲームの種類」という、2つの因子に関して、交互作用がないと予想されている為、繰り返しなしの二元配置を使って分散分析していきます。
先ほどと同様に「データ」タブから「データ分析」ツールを開いて、①「分散分析：繰り返しのない二元配置」を選択して、②「OK」をクリックします。
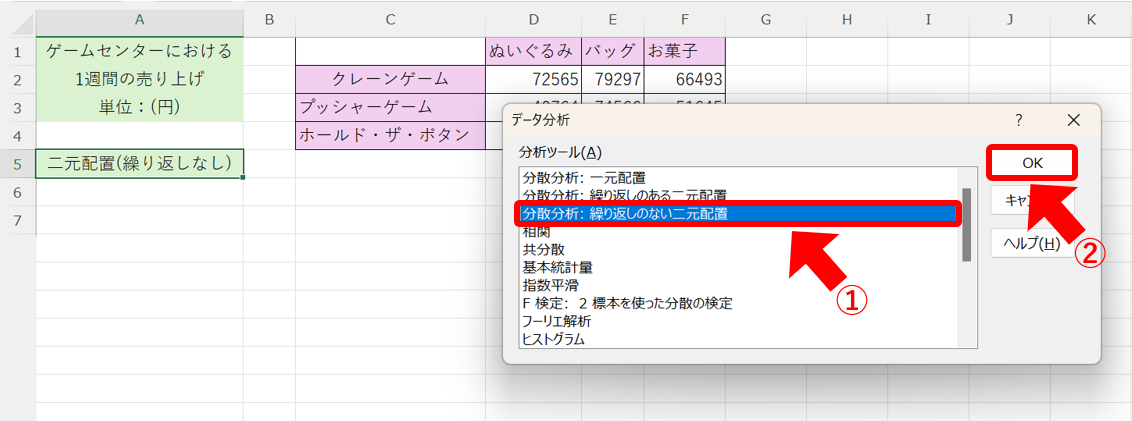
次に、③データ範囲を選択して、④ラベルが含まれるため、「ラベル」にチェックを入れます。
最後に、⑤「OK」をクリックします。
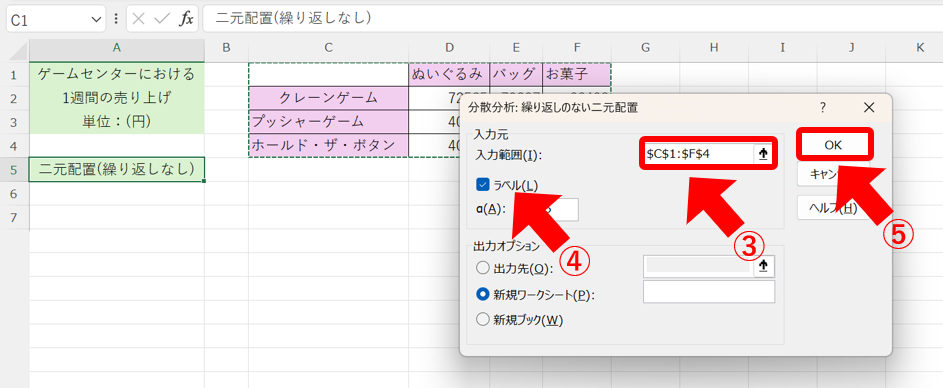
すると、別のページに以下の様に分散分析表等のデータが表示されます。
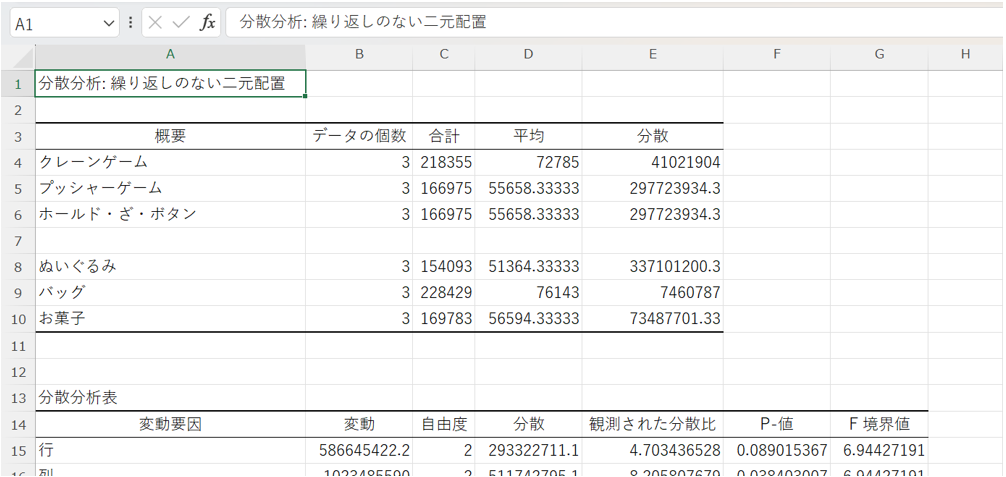
下にスクロールして、分散分析表のp値を確認すると、以下の様に2つのp値が確認できます。
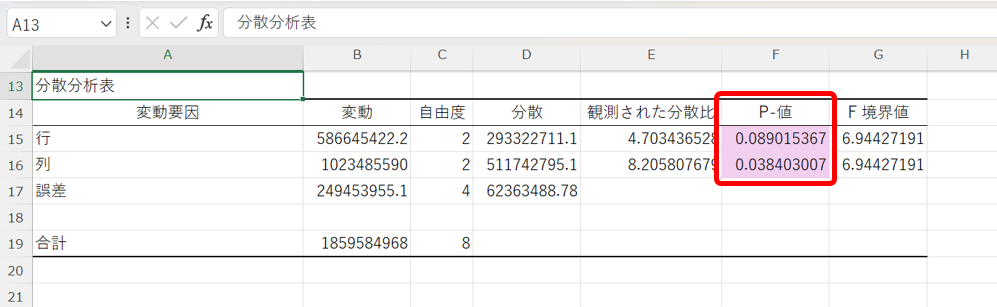
この結果のp値より、列、つまり、「景品の種類」間の母平均の差は有意であるものの、「クレーンゲームの種類」間の母平均の差は有意でないと判断できます。
つまり、交互作用が無いと予想すると、「景品の種類」のみが売り上げに関わっていると判断できます。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
まとめ
今回のExcelによる統計解析講座第12章では、分散分析を用いた、3つ以上の母集団の母平均の差についての仮説検定について解説してきました。
この分散分析は、複数の母集団について比較して、問題の主な要因となっているものを見つけ出すことが出来ます。
その為、実際のデータ分析の現場でも非常に有用な分析となっています。
次章では、単回帰分析や重回帰分析を含む、回帰分析について解説していきます。
分散分析に繋がる部分もありますので、是非読んでみて下さい！
