【回帰分析】Excelを使って単回帰分析と重回帰分析を解説！

前ページ

第13章では、単回帰分析や重回帰分析を含む、回帰分析について解説していきます。

回帰分析では、どのような要素がどのくらい結果に影響しているかを調べる事が出来、マーケティングなどにも用いられます。

非常に使い勝手のよい分析方法になりますので、是非習得していってください！

また、本章で用いるExcelファイルは以下からダウンロードして下さい！

ファイルをダウンロード

回帰分析とは

回帰分析とは、目的変数yと説明変数xの関係を明らかにする事で、どの説明変数xの表す要素がどれほど目的変数yに影響しているかを分析する手法です。

主な回帰分析の種類として、単回帰分析と重回帰分析があります。

この単回帰分析は、説明変数\(y\)に対して、説明変数\(x\)を1つ設定して、その関係性を係数\(b_{0},b_{1}\)を用いて以下の式の様にして表わす回帰分析です。

\[ y = b_{0}+b_{1}x_{1} \]

この様に、回帰分析で得た式を回帰式と言い、\(b\)の様な係数を回帰係数と言います。

ここで、実際のxをこの式に代入した時のyが、実際のyに近くなる様な式であればあるほど、単回帰分析が上手くいっていることになります。

これに対し、重回帰分析は、説明変数\(y\)に対して、説明変数\(x\)を複数設定して、その関係性を係数\(b_{0}, \cdots ,b_{k}\)を用いて以下の式の様にして表わす回帰分析です。
ただし、kは自然数とします。

\[ y = b_{0}+b_{1}x_{1}+\cdots+b_{k}x_{k} \]

この時、重回帰分析における\(b\)の様な係数を偏回帰係数と言います。

一般的に、この偏回帰係数が大きい説明変数xほど、目的変数yへの影響が大きくなります。
※例外は後ほど説明します。

以下、これらの単回帰分析と重回帰分析について説明していきます。

単回帰分析

寄与率(決定係数)

目的変数yの変動の内、回帰によって説明できる(=説明変数xで説明できる)割合を寄与率(決定係数)と言い、\(R^{2}\)で表します。

この寄与率(決定係数は)、回帰式が役に立ちそうかどうかを判断するのに使う事が出来ます。

この寄与率は、0から1の値をとり、1に近い程、単回帰分析の直線の当てはめが上手くいっているという事が出来ます。

また、寄与率(決定係数)は以下の式で計算できます。
ただし、\(S_{AB}\)はAとBの偏差積和です。

\[ R^{2}=\frac{S_{xy}^{2}}{S_{xx}S_{yy}} \]

決定係数に関してはExcelの関数を用いて瞬時に計算できる為、この式は覚えなくても大丈夫です！

残差

回帰式が役に立つかどうかを判断するにあたって、決定係数だけでは不十分です。

その為、目的変数yの値と、回帰で予測したyの値との差を考えます。

これを残差と言い、以下の式で計算されます。

残差 ＝ 実際のyの値 ー 予測したyの値

ここで、この残差はデータ数分ある為、その平均的な残差の大きさを把握するために残差の標準偏差を求めます。

このようにして、回帰分析で得られた回帰式が役に立ちそうかどうかは、決定係数と残差の標準偏差を算出する事で、調べる事が出来ます。

重回帰分析

自由度調整済み寄与率

寄与率(決定係数)の平方根Rを重相関係数と言います。

ここで、このRは説明変数が多くなると大きくなってしまいます。

その為、重回帰分析では、自由度調整済み寄与率というものが使われ、以下の式で計算できます。
ただし、データ数をnとします。

\[ R^{*2} = \frac{n-1}{n-k-1} (1-R^{2}) \]

また、自由度二度調整済み寄与率として、以下の式が使われる事もあります。

\[ R^{**2} = 1 – \frac{n+k+1}{n+1} \frac{n-1}{n-k-1} (1-R^{2}) \]

T値とp値

これまでの仮説検定に引き続き、回帰式の有用性の判断にも、T値とp値が用いられます。

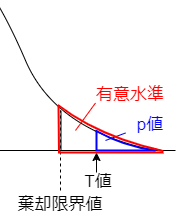
この回帰式の有意性判定において、帰無仮説と対立仮説は以下の様になります。

帰無仮説：\(x_{j}\)は\(y\)の予測に役立たない

対立仮説：\(x_{j}\)は\(y\)の予測に役立つ

この時、T値が大きい程、またはp値が小さい程、帰無仮説が棄却出来て、\(x_{j}\)の\(y\)への影響が大きいと判断できます。

※帰無仮説を棄却する基準についても、基本は有意水準5%です。
しかし、重回帰分析では有意水準5%は厳しく、T値では\(\sqrt{2}\) 前後、p値では0.2前後を基準にするという人もいます。

ダミー係数

「〇」や「×」、「晴れ」と「曇り」と「雨」の様に、数字ではなく、”質的”な変数(質的変数)を用いる場合には、これらにダミー変数を対応させて重回帰分析を行います。

このダミー変数は0か1しか取らない人工変数で、「〇」や「×」に対して、「1」と「0」を割り当てる、といったようにして、質的変数を数字として扱います。

また、「晴れ」と「曇り」と「雨」の様な3つのデータに関しては、以下の様にして、数字として扱います。

天気	\(x_{1}\)	\(x_{2}\)
晴れ	0	0
曇り	1	0
雨	0	1

多重共線性

重回帰分析を行う際に、最も気をつけなければならないのが、多重共線性です。

重回帰分析において、各説明変数は独立、つまり、相関が非常に小さい事が求められます。

この多重共線性とは、説明変数間に相関があり、互いに独立でない事を言います。

もし多重共線性が存在してしまうと、偏回帰係数に問題が起きて回帰式が求まらない、有用な説明変数のp値でも高く出る等、様々な問題が起きてしまいます。

そのため、重回帰分析で用いる説明変数に対しては、以下に説明する、相関行列を用いて、その独立性を調べる必要があります。

相関行列

相関行列とは、以下の様に、説明変数及び目的変数間の相関関係を表したものです。

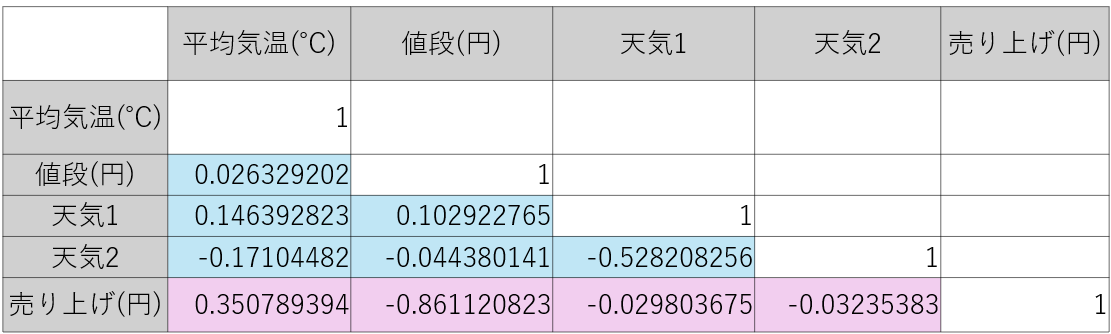
このとき、多重共線性を調べるには、説明変数同士の相関関係を見れば良いため、青の部分に注目します。

今回の例では、各々の説明変数に大きな相関は見られませんが、この青の部分の値の絶対値が1に近い値になった時、多重共線性が起こっている可能性があります。

なお、もし多重共線性が見られた場合は、
・独立でない説明変数同士を統合する
・独立でない説明変数の片方を除外する
等の処置を行う必要があります。

Excelを使って実際に回帰分析をしてみよう！

単回帰分析

まずは、Excel関数を用いて単回帰分析を行っていきましょう！

まず、回帰式を求めていきます。

\( y=b_{0}+b_{1}x_{1} \)の回帰係数\(b_{0},b_{1}\)に関して、

まず、\(b_{0}\)は以下の様にして計算する事が出来ます。

次に、\(b_{1}\)は以下の様にして計算する事が出来ます。

これを用いて2つの値について計算を行うと、以下の様になります。

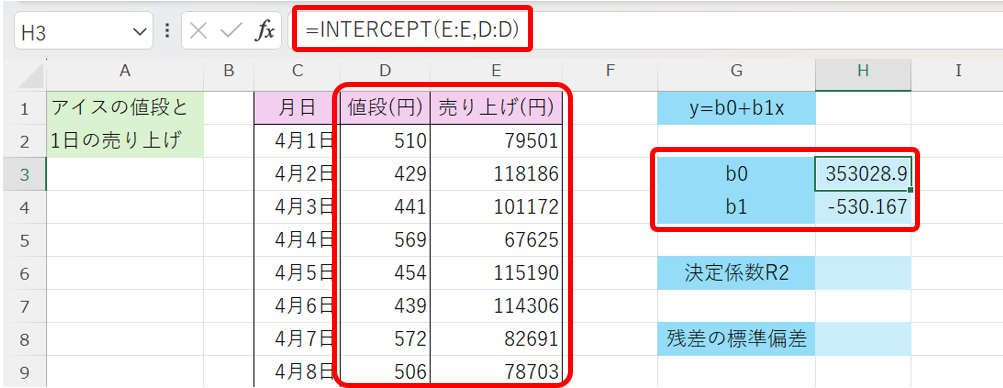
よって、回帰式は

\[ y = 353028 – 530.167x \]

で表せることが分かります。

次に、この回帰式の有意性を確認するために、決定係数を考えます。

決定係数は、以下の様にして計算する事が出来ます。

これを用いて計算を行うと、以下の様になります。

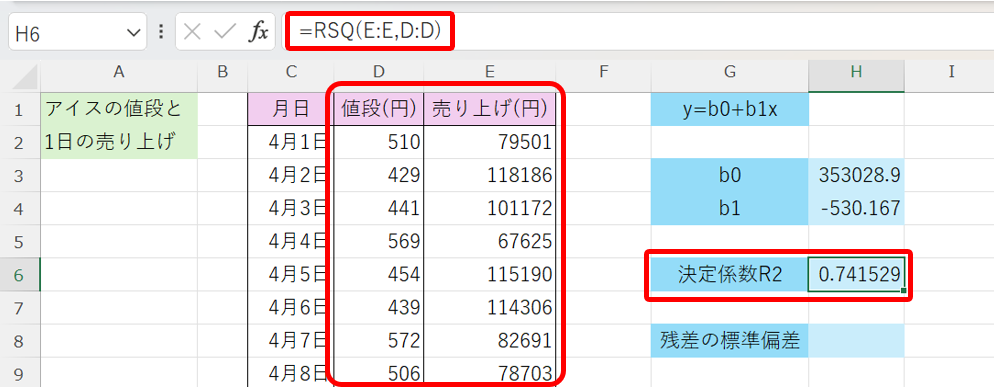
この結果から、売り上げの約74%はアイスの値段で説明できる(予測できる)事が分かります。

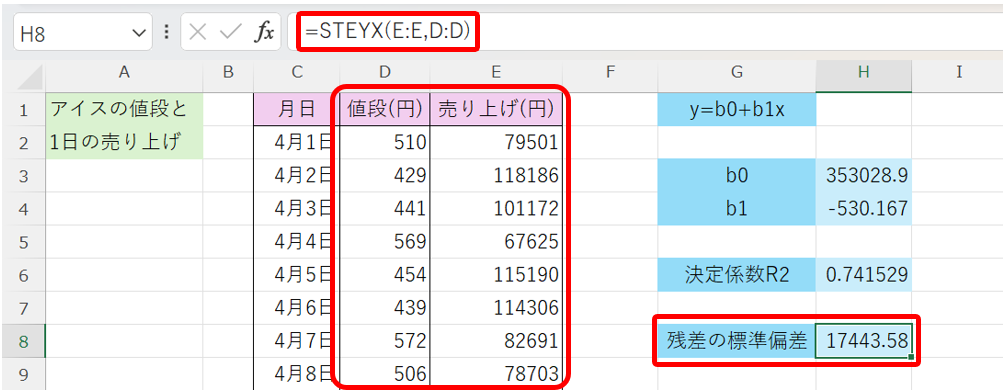
続いて、残差の標準偏差を考えます。

残差の標準偏差は、以下の様にして計算する事が出来ます。

これを用いて計算を行うと、以下の様になります。

グラフを用いた単回帰分析

例題1の単回帰分析に関して、回帰分析と決定係数の値だけであれば、Excelのグラフでも簡単に求めることが出来ます。

では早速、Excelファイル2ページ目を使ってやっていきましょう！

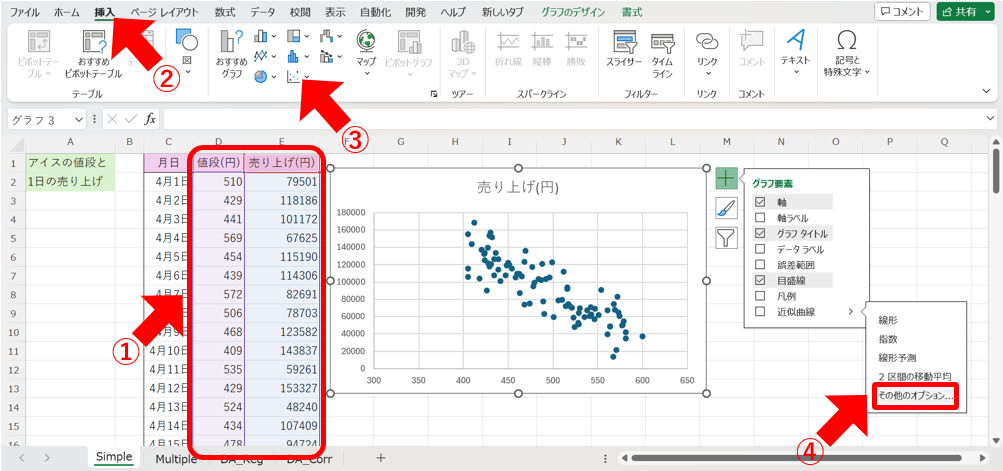
まず、①データ範囲を選択して、②「挿入」タブから③散布図を選択してグラフを作成します。

ここでは、データを見やすくするため、横軸の表示範囲を調整しています。

これらについて、詳しくは、第4章：【棒,折れ線,散布図】Excelの基本的なグラフを解説！、第6章：【プレゼン資料】Excelグラフの体裁の整え方について解説！をご参照下さい！

次に、④「近似直線」から「その他のオプション」を選択します。

続いて、⑤「グラフに数式を表示する」と「グラフにR-2乗値を表示する」にチェックを入れます。

数式や軸ラベルについては、見やすさの為に調整しています。

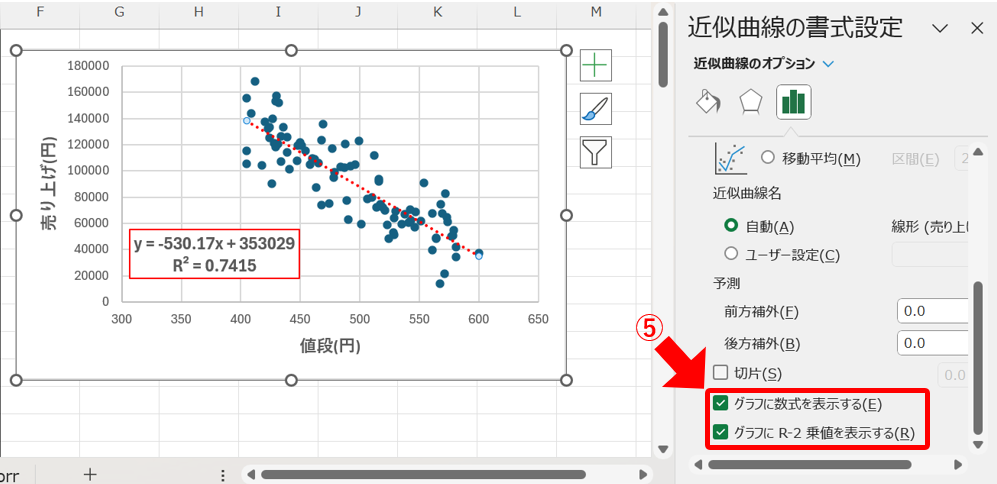
これより、回帰式と決定係数を簡単に求める事が出来ました。

値を見ると、先ほど算出した数と等しい事が分かります。

(参考)正規確率プロット

第8章の【確率変数・正規分布】確率変数や正規分布をExcelで解説！で触れましたが、単回帰は、データが正規分布に従っているかを調べる事が出来ます。

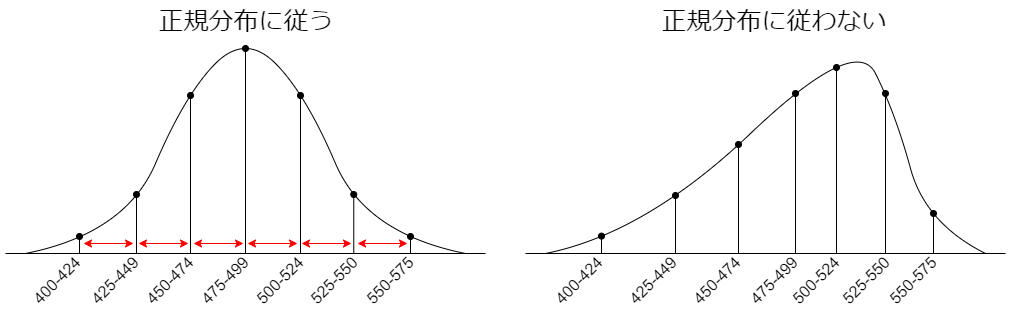
データが正規分布に従う為には、中央値付近で平均値を取り、中心から離れるにつれて、左右対称に、そのデータ数が少なくなっていくような曲線分布である必要があります。

これについて、データが正規分布に従う時、度数分布表の各階級値における、累積相対度数に対応するz値が等間隔で並びます。

そしてこの時、等間隔の階級値と等間隔のz値の関係は、単回帰分析の回帰式で精度良く表す事が出来ます。

これを用いて、正規分布に従うかを判断する事が出来るものを正規確率プロットといいます。

中心極限定理より、データ数が十分多い時は、調べずとも正規分布に従うとみなせます。

そのため今回は、Excelファイル3ページ目の、アイスの値段のデータから25個のみ抜き出したデータについて、正規性を確認してみましょう！

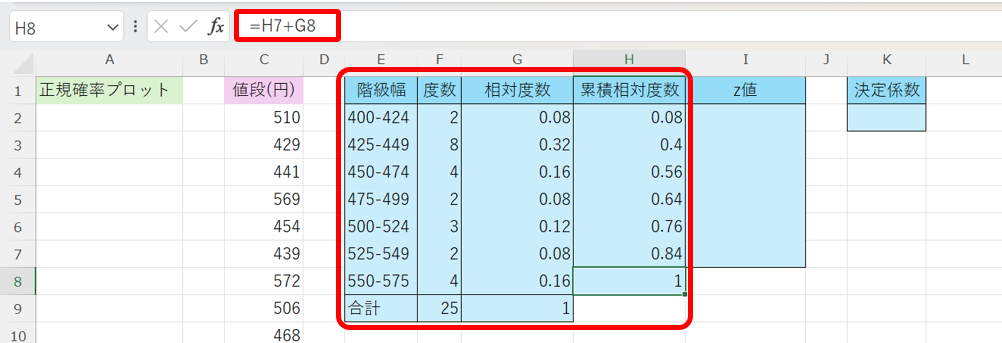
まず、度数分布表を作成して、累積相対度数を算出します。

これらの値の導き方に関して、度数にはCOUNTIF関数とCOUNTIFS関数を、合計にはSUM関数を使っています。

詳しくは、Excelファイル3ページ目のデータを見てみて下さい！

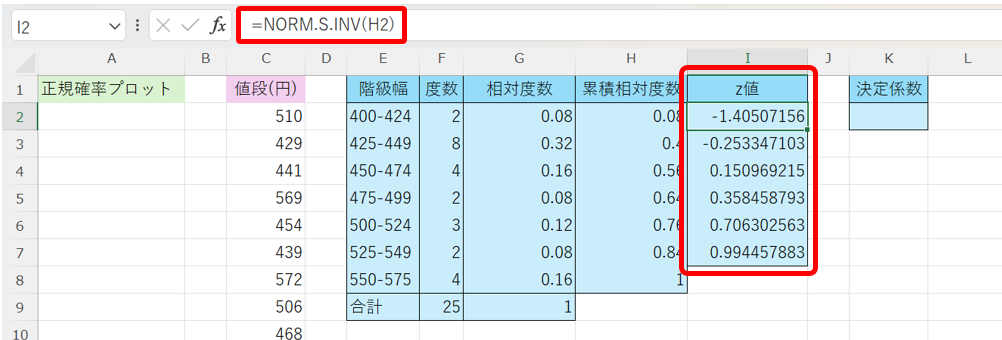
次に、累積相対度数に対応するz値を算出します。

z値を算出するには、NORM.S.INV関数を使います。

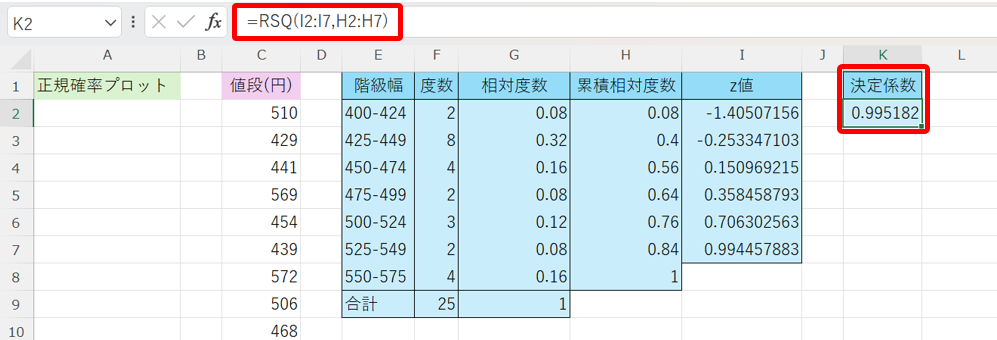
最後に、累積相対度数とz値の関係について、決定係数を算出します。

また、グラフで正規確率プロットを確認すると、以下の様になります。

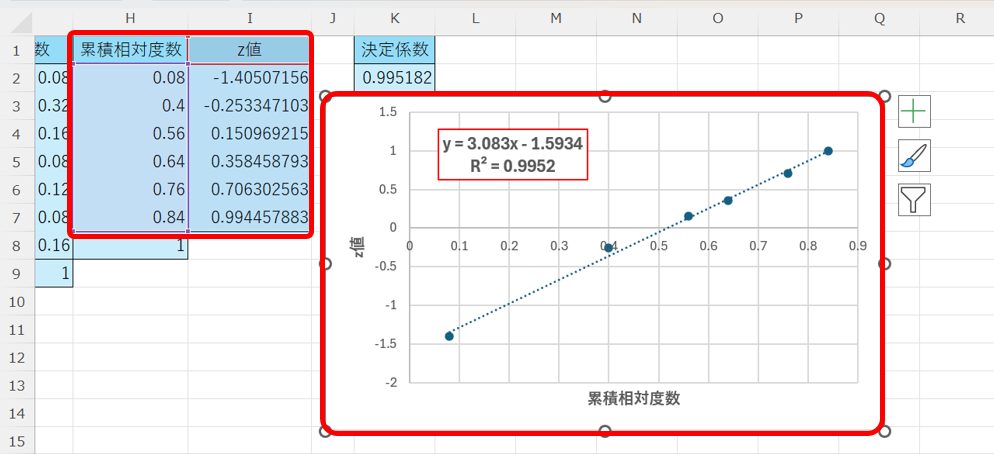
ここで、データが正規分布に従っているかの判断基準は、「決定係数が0.99以上かどうか」で行います。

この時、このデータは正規分布に従っていると判断できます。

※この決定係数の基準は、統計学的には定まっておらず、経験則によるものです。

データ分析ツールを用いた重回帰分析

最後に重回帰分析について、データ分析ツールを使って考えてみましょう！

このデータ分析が何かわからない方は、第7章：【相関分析】相関係数と共分散をExcelを用いて解説！の共分散と相関係数のデータ分析ツールを用いた算出方法を参照して設定してみて下さい！

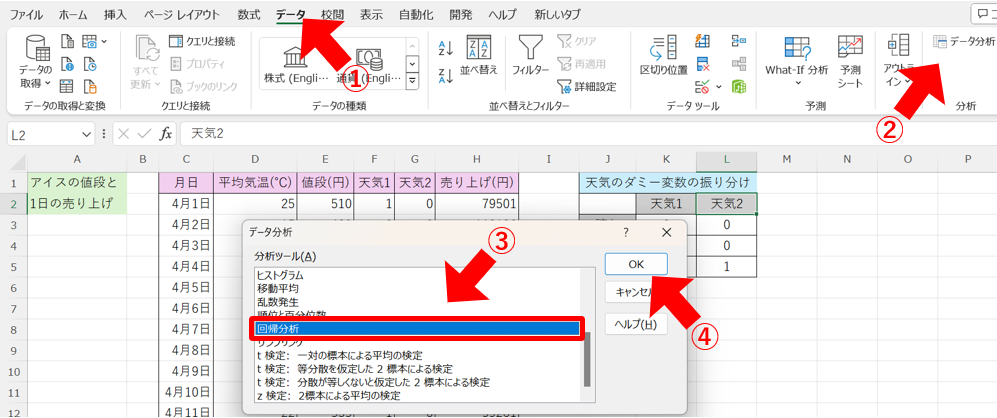
まず、①「データ」タブから、②「データ分析」ツールを選択し、更に③「回帰分析」を選択して④「OK」をクリックします。

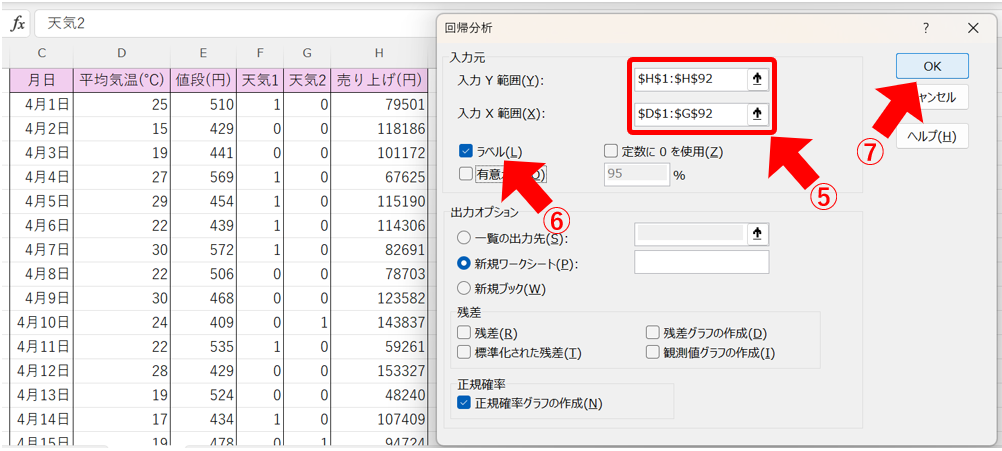
次に、⑤「入力Y範囲」に「売り上げ」の、「入力Y範囲」に「平均気温」「値段」「天気1」「天気2」を入れ、⑥ラベルを含むため「ラベル」にチェックを入れ、⑦「OK」をクリックします。

すると、以下の様に新しいシートに重回帰分析の結果が出力されます。

ここで、まず、「補正R2」に注目します。

これは、自由度調整済み寄与率の事です。

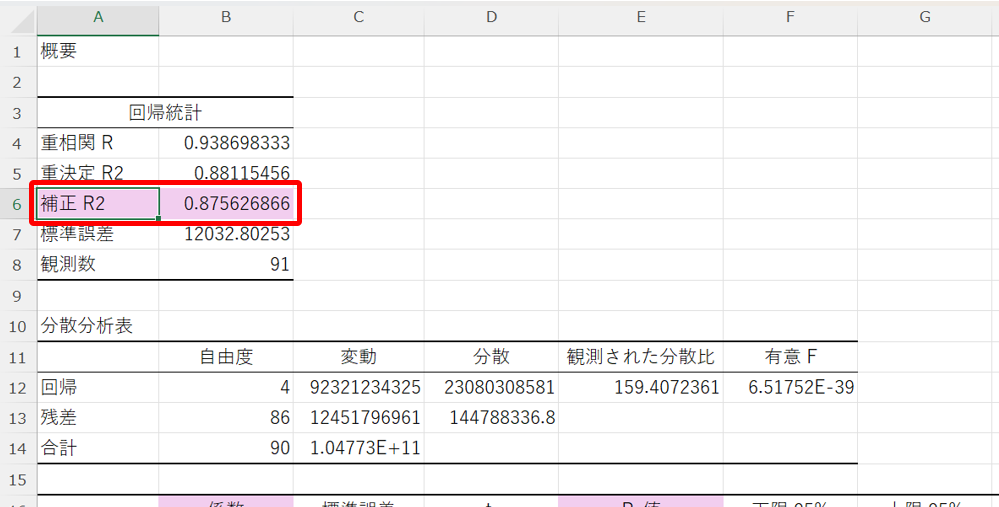
この、補正R2(自由度調整済み寄与率)を見ると、目的変数の約87.6%がこの回帰式で説明できることが分かり、先ほどの単回帰分析より高くなっている事が確認できます。

次に、係数とp値について確認します。

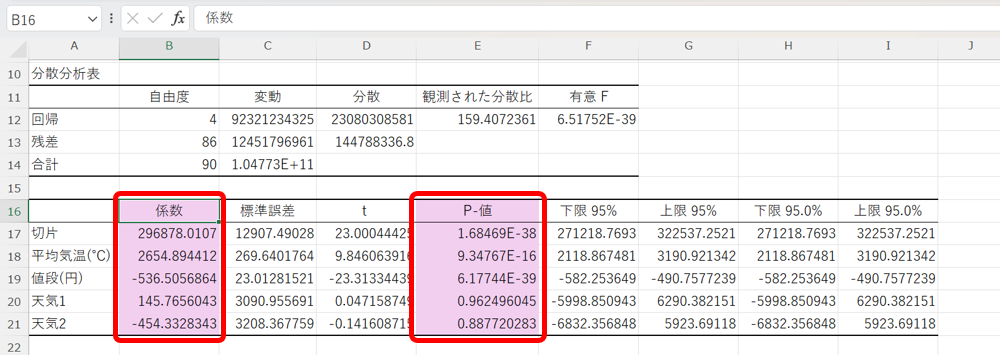
まず、係数に関して、これは、偏回帰係数の事で、この絶対値が大きい時、その説明変数が売り上げ(目的変数)に寄与する割合が高くなります。

更にp値に関して、この値が小さい程、その説明変数が目的変数に寄与するという事が出来ます。

更に、今回の有意水準を5%とすると、「平均気温」と「値段」に関しては、p値が0.05を下回っているものの、「天気1」と「天気2」に関しては、p値が大きくなっています。

そのため、「天気1」と「天気2」は目的変数の説明に役立っていないと判断する事が出来ます。

ここで、先程のデータ分析ツールにおいて、以下の様に、「天気1」と「天気2」を説明変数から除いて、結果を出力してみます。

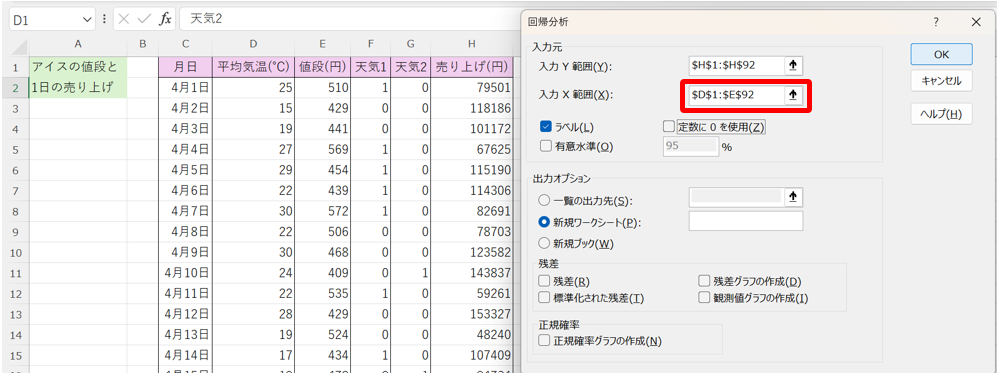
すると、以下の様になります。

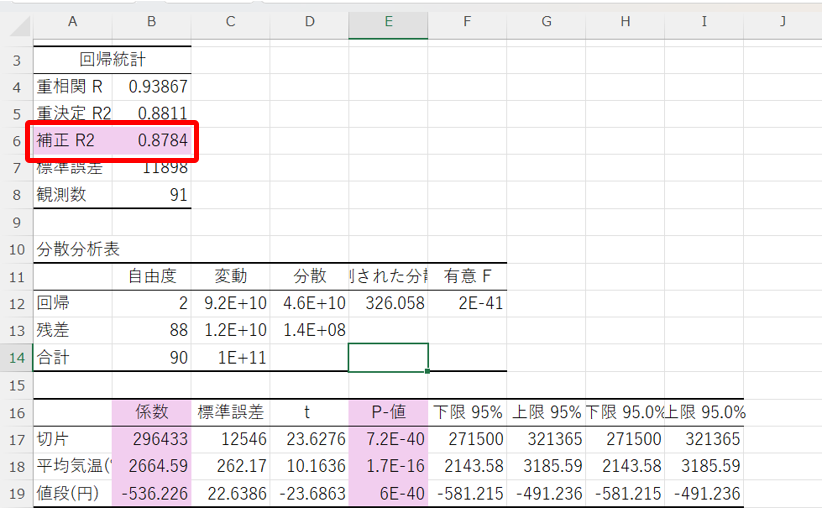
この結果から、補正R2が約87.8%で（今回は少しだけ）上がり、先程の回帰式より少し良くなったことが確認できます。

このように、関係ない説明変数は除外して回帰分析を行うと、より良い結果が得られることがあります。

最後に、多重共線性について調べます。

先程と同じで順で、①「データ」タブから「データ分析」ツールを選択し、②「相関」を選択して③「OK」をクリックします。

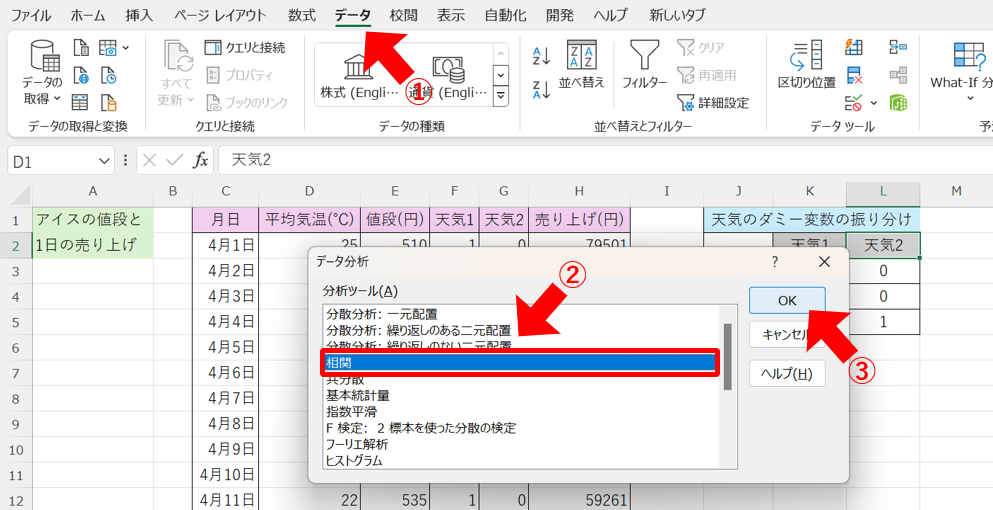
次に、④データ範囲を選択して、⑤「先頭行をラベルとして使用」にチェックを入れて、⑥「OK」をクリックします。

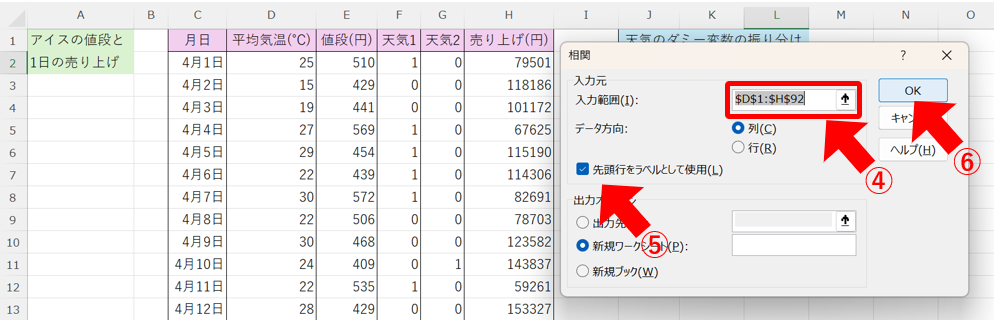
すると、新しいシートに、以下の様に相関行列が出力されます。

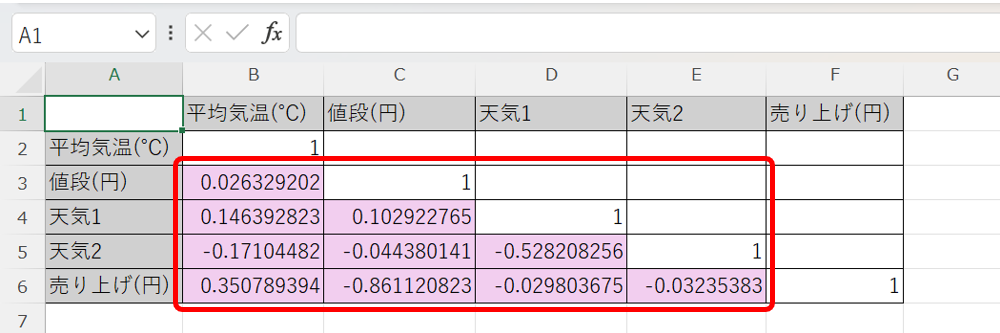
ここで、説明変数間の相関についてみてみると、際立って大きいものはなく、説明変数は独立であったという事が出来ます。

まとめ

今回のExcelによる統計解析講座第13章では、回帰分析として、単回帰分析及び重回帰分析の概要とExcelでの使い方について解説してきました。

この回帰分析は、原因分析や予測において、一般的な分析方法となっており、その汎用性も高くなっていますので、是非、身に付けていってください！

本章で、Excelによる統計解析講座は終わりです。

もし分からない部分があったら、前の章を見なおして、データ分析の基礎を付けていただければと思います！