第7章からは、統計分野に踏み込んで、実際にデータ分析について触れていきます!
統計・数学が苦手な人でも理解できるように心がけて説明していきますので、是非ついてきてください!
本章では、統計学に基づいたデータ分析の先駆けとして、共分散と相関係数について解説します!
高校の数学Ⅰで習う範囲なので、忘れかけた記憶を呼び起こしながら読んでいって下さい!
以下の記事では、「共分散」「相関係数」についてより詳しく解説しています。

今回用いるファイルは以下からダウンロードして下さい!
本連載講座【Excelによる統計解析講座】では、Excel未経験の方、自身の無い方でも順を追って学習でき、基礎からデータ分析に必要なスキルまでを身に付ける事が出来ます。
画像が多く、ビジュアルで理解しやすくなっておりますので、読み物が得意ではないという方も大丈夫です!
また、第7章からは、統計学の分野も扱う為、様々な方に役立つ講座となっております。
そのため、
- Excelを仕事で使う可能性のある方
- Excelに自信のない方
- データ分析をExcelでやりたい方
等は是非、TechTeacherが運営する【Excelによる統計解析講座】を使って学習していって下さい!
〈目次〉
第1章:【テーブル】Excelのテーブル(フィルター)を解説!
第2章:【SUM,AVERAGE】Excelの基本的な関数を解説!
第3章:【XLOOKUP,COUNTIF】データ分析の為のExcel関数を解説!
第4章:【棒,折れ線,散布図】Excelの基本的なグラフを解説!
第5章:【ピボットテーブル】Excelの便利機能”ピボットテーブル”を紹介!
第6章:【プレゼン資料】Excelグラフの体裁の整え方について解説!
第7章:【相関分析】相関係数と共分散をExcelを用いて解説!
第8章:【確率変数・正規分布】確率変数や正規分布をExcelで解説!
第9章:【t検定・z検定】母平均と母分散の仮説検定について解説!
第10章:【t検定・z検定】2つの集団の母平均・母比率の仮説検定を解説!
第11章:【仮説検定】カイ二乗検定とF検定をExcelで一瞬で解く!
共分散と相関係数の意味
今回紹介する、共分散と相関係数を理解する為に、まず、分散と標準偏差について触れていきましょう!
分散と標準偏差の意味
あるデータを考えた時に、そのデータの平均との距離を偏差といい、以下で計算できます。
偏差=データ値ー平均
そして、この偏差の平均を取る事でデータのばらつき具合を調べようとするのが、分散と標準偏差です。
あるデータの集まり\(\{x_{1}, x_{2}, \cdots , x_{n}\}\)とその平均\(\bar{x}\)に関して、偏差の2乗平均を取ったものを分散と言い、これを\(S^{\scriptsize{2}}\)として、以下の計算式で表す事が出来ます。
\[S^{\scriptsize{2}}=\frac{\text{各データの偏差の2乗}}{\text{データ数}}=\frac{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}}{n}\]
更に、分散の平方根を取ったものを標準偏差といい、これを\(\sigma\)として、以下の式で表す事が出来ます。
\[\sigma=S=\sqrt{S^{\scriptsize{2}}}\]
分散と標準偏差の大きな違いは、元の単位が保存されるか否かにあります。
例えば、身長のデータ(単位:\(cm\))について分散と標準偏差を考えると、分散の単位は\(cm^{2}\)、標準偏差の単位は\(cm\)となります。
分散と標準偏差について、その大きさは単位や規模に大きく左右されるため、値を比較する際には注意が必要です。
例えば、身長のデータの単位を\(cm\)から\(mm\)に変えると、元のデータの大きさは10倍になり、分散の値は100倍、標準偏差の値は10倍になってしまいます。
分散と標準偏差について詳しく知りたい方は、次の平均・分散とは?基本統計量を分かりやすく解説!をチェックしてみて下さい!

共分散の意味
2次元データにおいて、2つの属性(データ)の関係を相関関係と言います。
この時、下図(左)の様に、全体的に右肩上がり(全体的な方向の傾きが正)の関係を正の相関、下図(右)の様に、全体的に右肩下がり(全体的な方向の傾きが負)の関係を負の相関と言います。
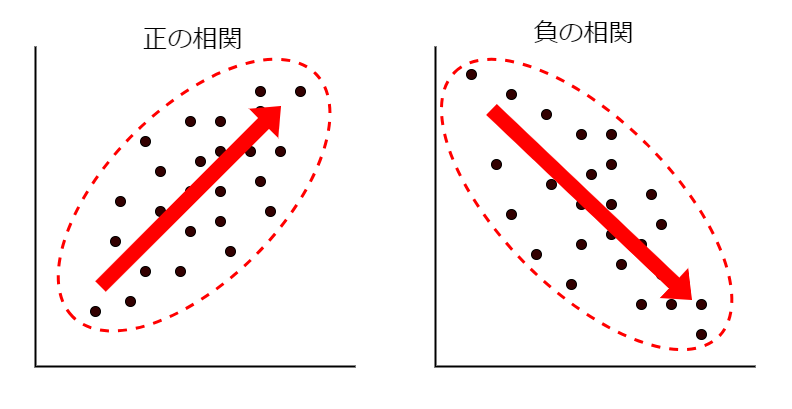 この時、データに正の相関があるのか、負の相関があるのかを表すのが、共分散です。
この時、データに正の相関があるのか、負の相関があるのかを表すのが、共分散です。
ここで、共分散(=Covariance)は、Cov(x,y)で表され、2次元データ\((x,y)=(x_1,y_1),\cdots,(x_n,y_n)\)の偏差の平均として、以下の式で定義されます。
\begin{equation}
\begin{split}
Cov(x,y)
&=\frac{\text{xの偏差}\times\text{yの偏差}}{\text{データ数}} \\
&=\frac{(x_{1}-\bar{x})\times(y_{1}-\bar{y})+\cdots+(x_{n}-\bar{x})\times(y_{n}-\bar{y})}{n}
\end{split}
\end{equation}
この式について、
\( \text{「} x_n-\bar{x} \: >0 \text{かつ} y_n-\bar{y} \: >0 \text{」} \text{もしくは「}x_n-\bar{x} \: >0 \text{かつ}y_n-\bar{y} \: >0 \text{」} \)
\( \text{の時、} Cov(x,y)>0 \)
\( \text{「} x_n-\bar{x} \: >0 \text{かつ} y_n-\bar{y} \: <0 \text{」} \text{もしくは「}x_n-\bar{x} \: <0 \text{かつ}y_n-\bar{y} \: >0 \text{」} \)
\(\text{の時、} Cov(x,y)<0 \)
となり、これは以下の図から、共分散が正なら、灰色部分に属するデータが多いため正の相関が、共分散が負なら、白色部分に属するデータが多いため負の相関があることが分かります。
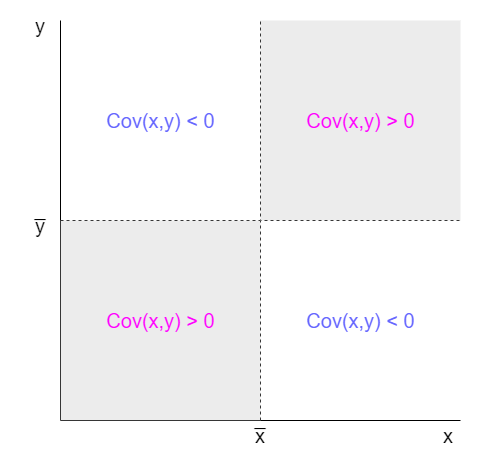
共分散の大きさは相関の”強さ”には関係ない事に注意しましょう。
共分散の定義式について、xを身長(\(cm\)のデータ、yを体重\(kg\)のデータとすると、共分散の単位は、「\(cm \times kg\)」となります。
しかしここで、xのデータ表記を\(cm\)から\(mm\)へ、yのデータ表記を\(kg\)から\(g\)に変換すると、xの値は10倍、yの値は1000倍になるため、結果的にデータは変わっていなくても、共分散の大きさは10000倍になります。
このように、共分散は単位に大きく左右される為、共分散の大きさは意味を成さない事に注意しましょう。
相関係数
共分散は、その値に単位を含む為に、相関の強さを推し量ることが出来ないのでした。
これに対して、単位を消去する事で相関の強さを-1から1までの数値で表したものが相関係数です。
ここで、相関係数(Correlation)は、その英語のrを取って、ギリシャ文字の\(\rho(x,y)\)で表され、2次元データ\((x,y)=(x_1,y_1),\cdots,(x_n,y_n)\)に対して、共分散をxの標準偏差とyの標準偏差で割った値として、以下の式で定義されます。
\[\rho(x,y)=\frac{\text{xとyの共分散}}{\text{xの標準偏差} \times \text{yの標準偏差}}=\frac{Cov(x,y)}{\sigma(x) \sigma(y)}\]
この時、相関係数の正負は共分散によって決まります。
また、定義式より、単位が消去されるため、以下の図の様に、相関の強さを数値で評価する事が出来ます。

\(\rho(x,y)=1\)の時(全てのデータが傾きが正の一直線上にある時)を正の完全相関といい、\(\rho(x,y)=-1\)の時(全てのデータが傾きが負の一直線上にある時)を負の完全相関といいます。
共分散と相関係数のExcel関数を用いた算出方法
ではついに、これらの値をExcelで算出していきましょう!
まずは、分散と標準偏差からです。
分散と標準偏差の算出方法
まず、Excelにおける、分散の関数は、以下の様になります。
=VAR.P(データの入力範囲)
これを用いて、T小学校の小学3年生の男子の身長の分散を算出してみましょう!
すると、下図の様に、分散の値が86.95である事が瞬時に計算できます。
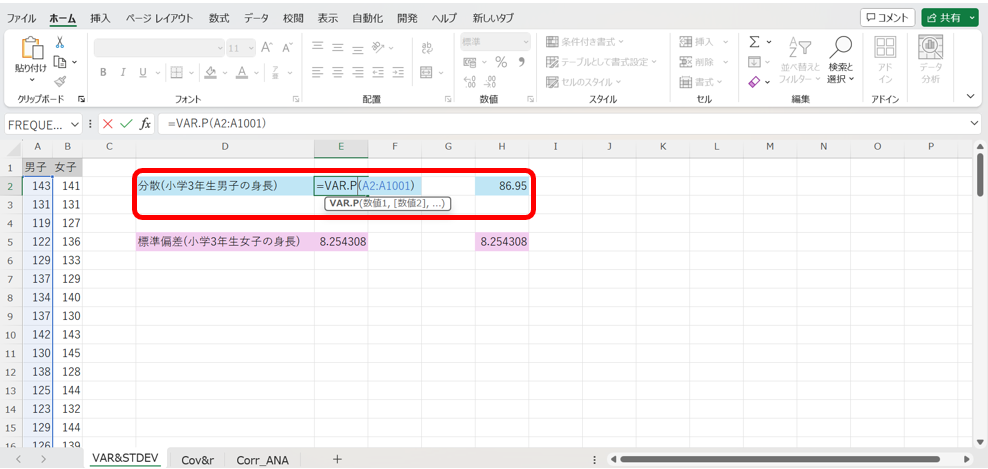
=VAR.P(データの入力範囲)の様に、”P”が付く関数をP関数と言います。
これは、母集団(Population)のPで、標本ではなく、母集団の分散を計算する事を示しています。
母集団や標本に関しては、第8章では話しますが、詳しく知りたい方は、以下の母集団・標本・区間推定とは?統計の基本用語をマスターしようをご覧ください!

次に、Excelにおける、標準偏差の関数は、以下の様になります。
=STDEV.P(データの入力範囲)
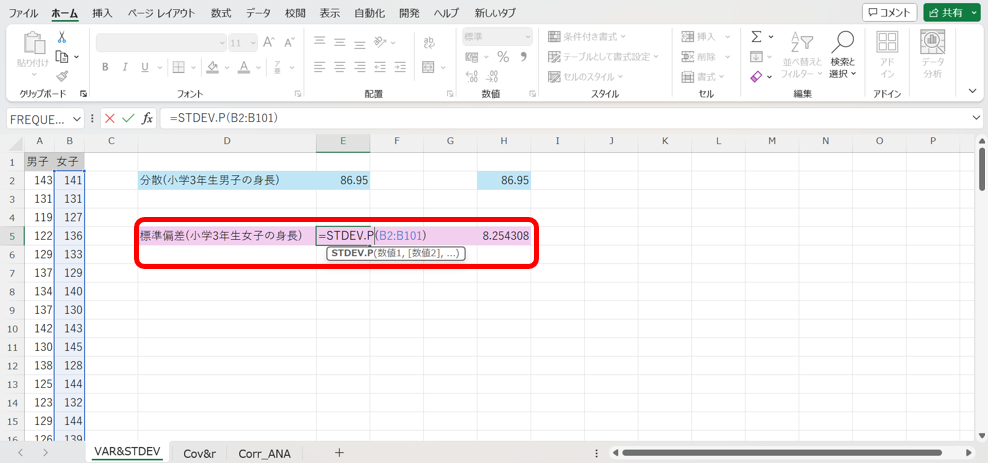
これを用いて今度は、T小学校の小学3年生の女子の身長の標準偏差を算出してみましょう!
すると、下図の様に、標準偏差の値が約8.25である事が瞬時に計算できます。
例題
T小学校の小学3年生に関して、Excelファイル1ページ目を使って、女子の身長の分散と、男子の身長の標準偏差もそれぞれ求めて、比較してみましょう!
まず、T小学校の小学3年生に関して、女子の身長の分散は以下の式を入力する事で計算する事が出来ます。
=VAR.P(B2:B1001)
この計算結果から、約68.13である事が分かります。
男子と女子のデータの単位が同じである事に留意すると、男子の身長の分散が86.95であったことから、女子の方が身長のばらつきが小さい事が分かります。
次に、T小学校の小学3年生の男子の身長の標準偏差は以下の式を入力する事で計算する事が出来ます。
=STDEV.P(A2:A101)
この計算結果から、約9.32である事が分かります。
こちらも男子と女子のデータの単位が同じである事に留意すると、女子の身長の標準偏差が約8.25であったことから、やはり女子の方が身長のばらつきが小さい事が分かります。
共分散の算出方法
では、今度は共分散の値をExcelで算出していきましょう!
Excelにおける、共分散の関数は、以下の様になります。
=COVARIANCE.P(x入力範囲,y入力範囲)
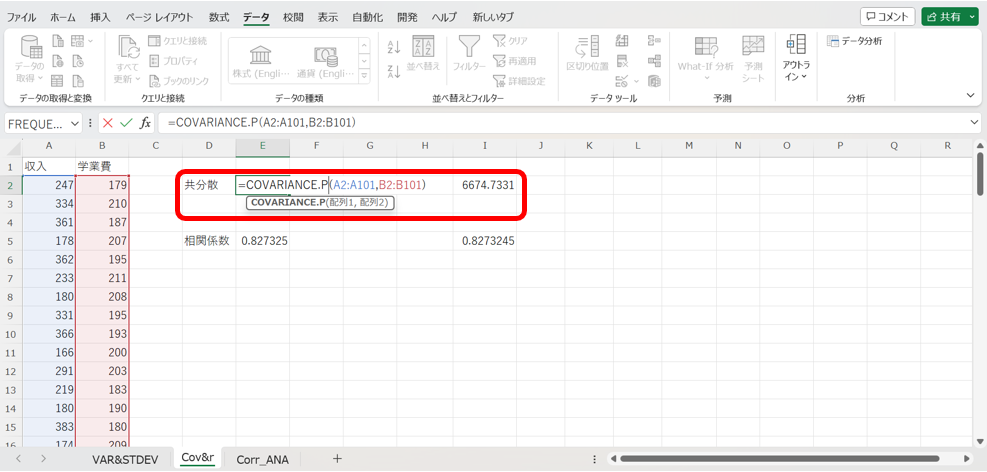
これを用いて、E公立幼稚園の世帯年収に対する学習費総額の共分散を算出してみましょう!
すると、以下の様に共分散の値が約6674.73である事が簡単に計算できます。
相関係数の算出方法
同様にして、相関係数の値もExcelで算出していきましょう!
Excelにおける、相関係数の関数は、以下の様になります。
=CORREL(x入力範囲,y入力範囲)
※ここではPが入らない事に注意しましょう!
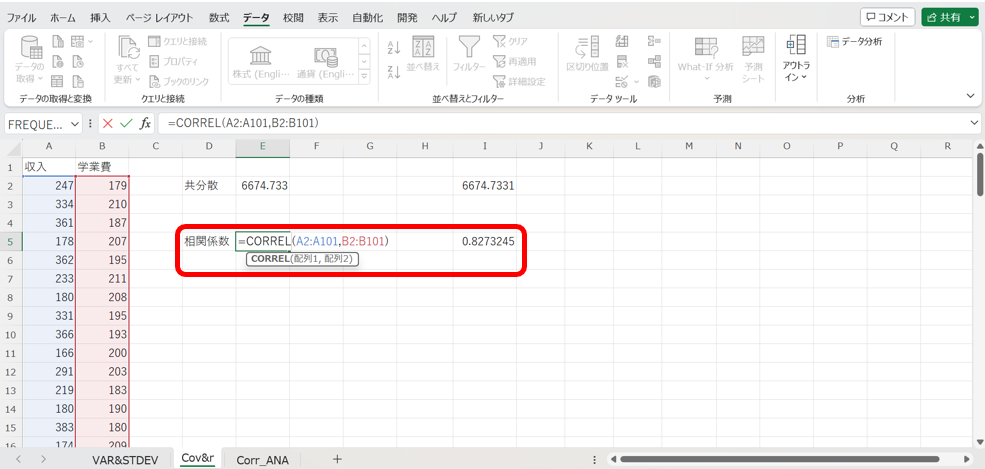
これを用いて、E公立幼稚園の世帯年収に対する学習費総額の相関係数を算出してみましょう!
すると、以下の様に相関係数の値が約0.83である事が簡単に計算できます。
共分散と相関係数のデータ分析ツールを用いた算出方法
Excelを用いたデータ分析の方法には、関数の他にも、データ分析ツールというものがあります。
これを用いると、求めたい統計値等を一瞬で計算する事が出来ます。
しかし、Excelの初期設定では、このデータ分析ツールは表示されていない為、WindowsとMacについてそれぞれ、これから一緒に設定していきましょう!
データ分析ツールの設定方法 (Windowsの場合)
Windowsでデータ分析ツールを設定するにはまず、①「ファイル」タブ→(その他→)オプションをクリックします。次に、②「アドイン」から、③「設定」をクリックします。
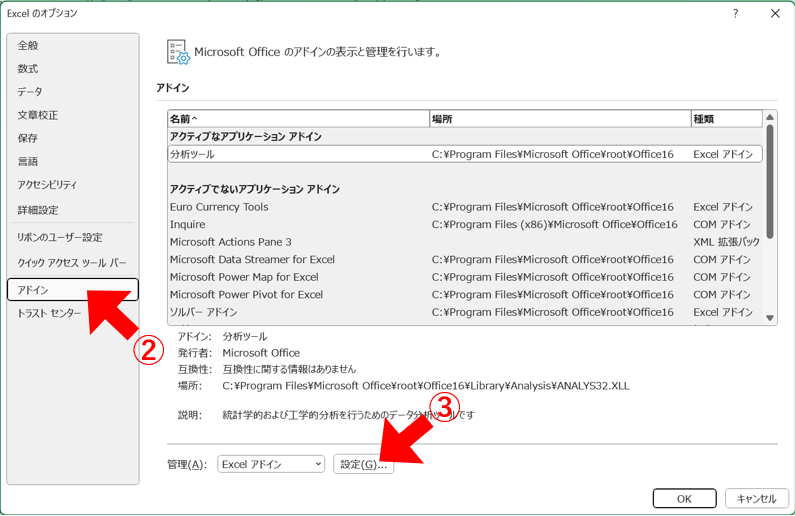
更に、④「分析ツール」にチェックを入れて、⑤「OK」をクリックします。
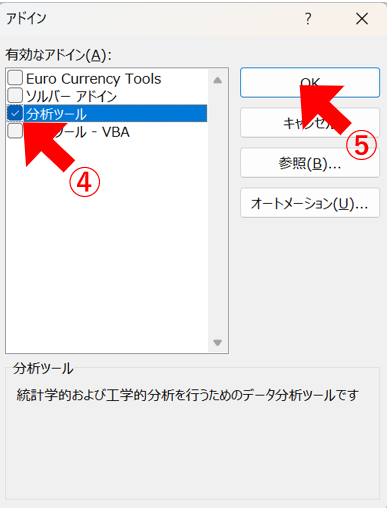
すると、以下の様に、データツールにデータ分析ツールが追加されます!

データ分析ツールの設定方法 (Macの場合)
同様にして、Macの場合のデータ分析ツールの追加方法も説明していきます。
と言っても、Macの場合は、非常に簡単です。
まず。①画面上部の「ツール」タブから、②「Excelアドイン」をクリックします。
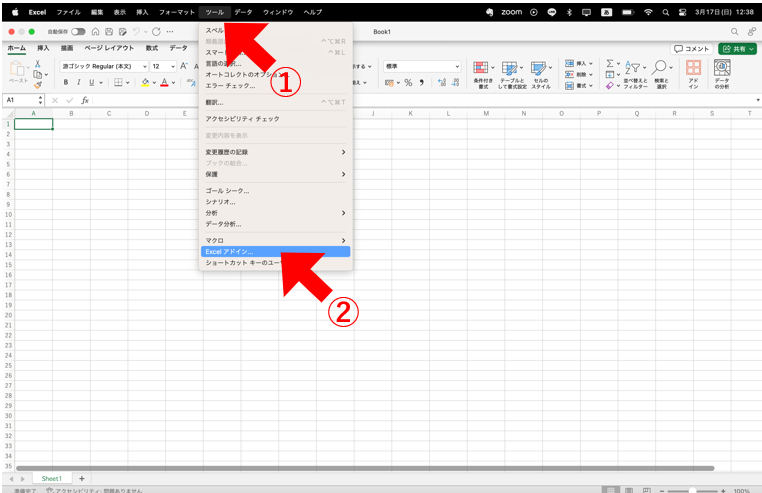
次に、③「分析ツール」にチェックを入れて「OK」を押すだけです。
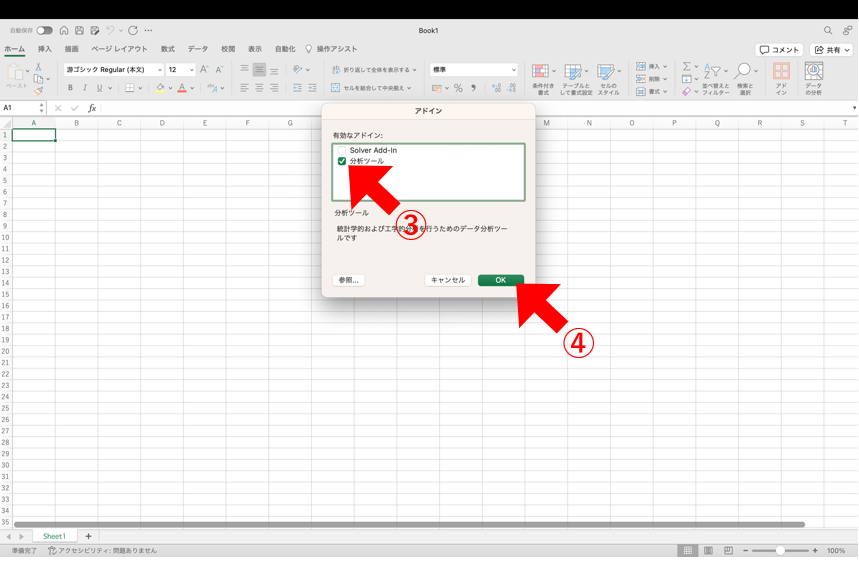
データ分析ツールを用いた共分散と相関係数の算出方法
では、今設定したデータ分析ツールを用いて、共分散を算出してみましょう!
まず、①「データ」タブから、②「データ分析」をクリックして、③「共分散」を選択し、④「OK」をクリックします。
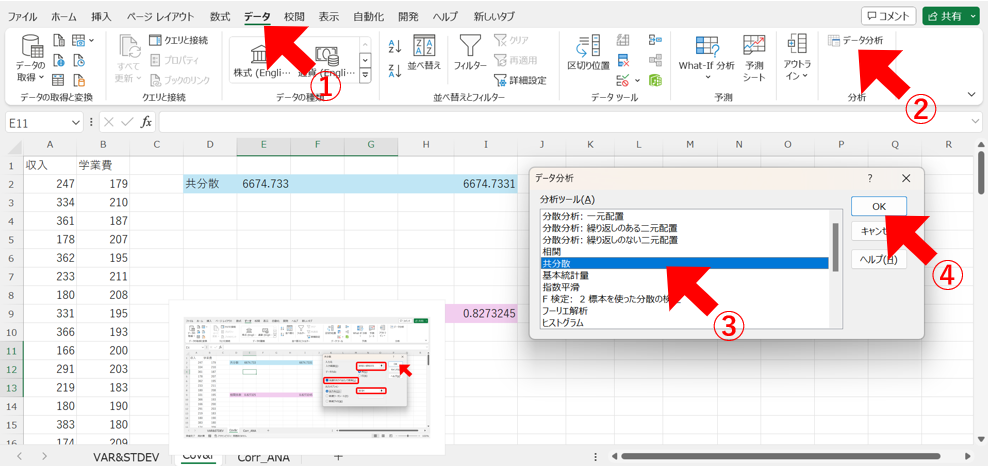
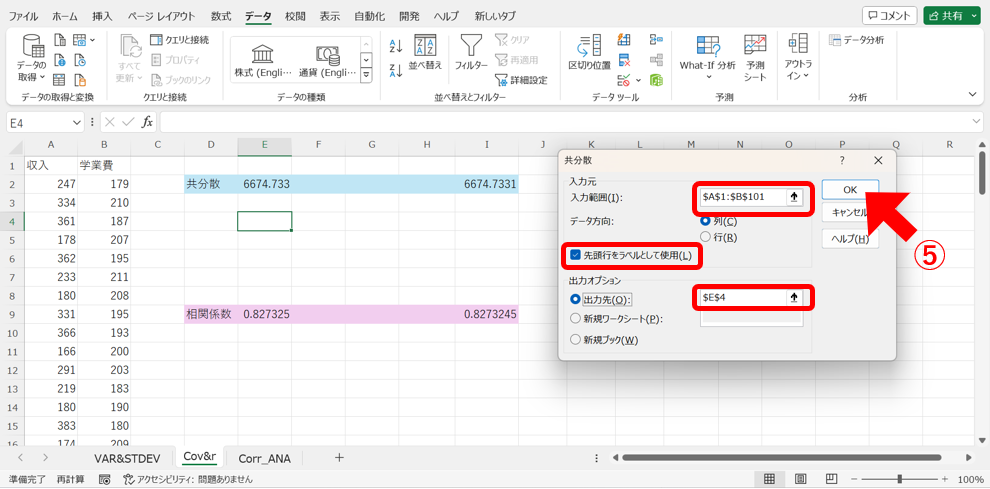
次に、⑤各項目にセルの範囲を入力して、「OK」を押します。
なおここでは、A列(収入)とB列(学業費)のセルを全て選択して、「先頭行をラベルとして使用」にチェックを入れ、出力先を共分散を求めたすぐ下に設定しています。
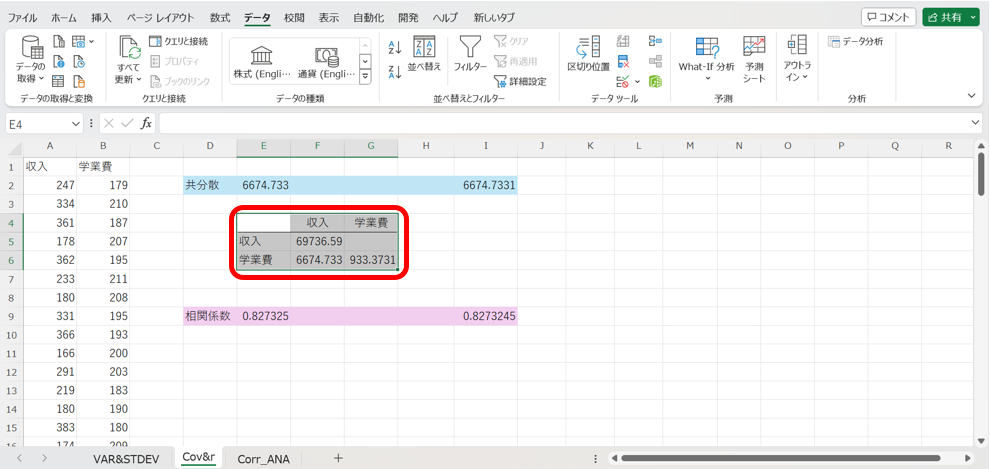
すると、以下の様に、収入と学業費の分散及び、共分散の値がまとめて出力されます。
※”収入”と”収入”の共分散は”収入の分散”になります。
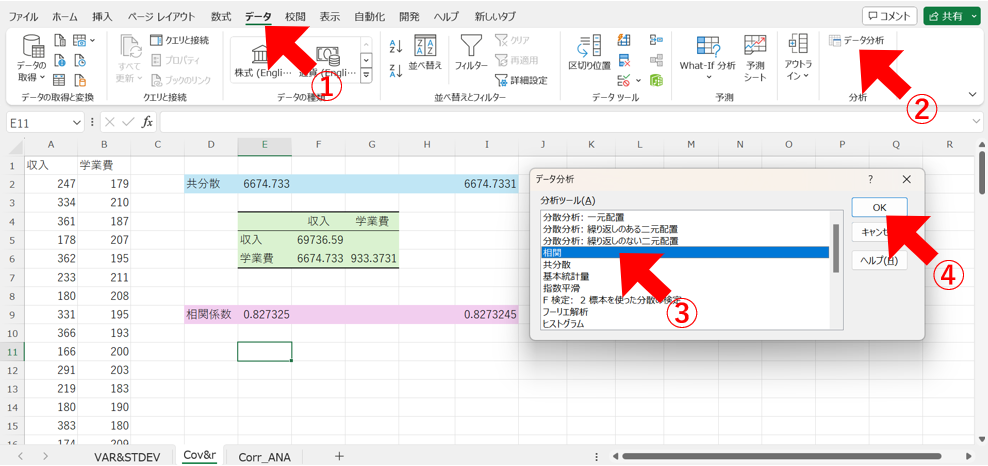
同様にして、相関係数の値も算出していきましょう!
①「データ」タブから、②「データ分析」をクリックして、③「相関」を選択し、④「OK」をクリックします。
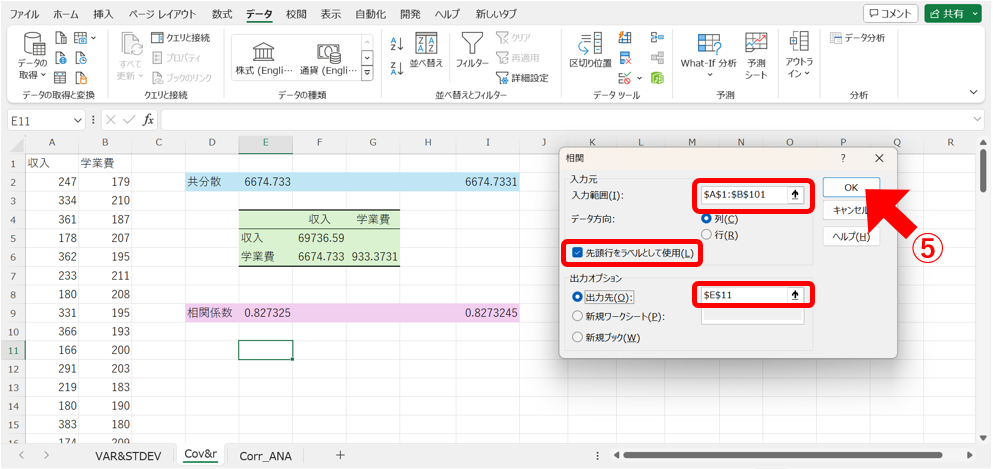
次に、⑤各項目にセルの範囲を入力して、「OK」を押します。
なおここでも、A列(収入)とB列(学業費)のセルを全て選択して、「先頭行をラベルとして使用」にチェックを入れ、出力先を相関係数を求めたすぐ下に設定しています。
すると、以下の様に、収入と学業費相関係数の値がまとめて出力されます。
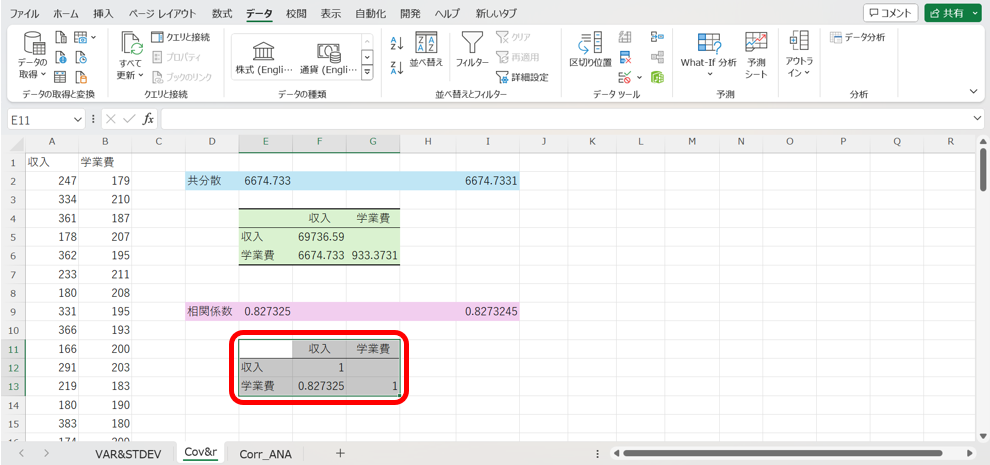
また、上の画像から、共分散と相関係数に関して関数による計算結果と一致している事が確認できます。
是非自分にやりやすい方を選んで、使ってください!
相関分析をやってみよう!
では実際にExcelファイル内の、2000年から2020年の日本人の総人口の推移のデータを用いて、自己相関分析をやってみましょう!
自己相関分析とは
日本の総人口の様に、同一の観測対象に対して時間を追って観測したデータを時系列データと言います。
この時系列データの分析には主に、ある時点でのデータとその数年後におけるデータを比較する、自己相関分析が用いられます。
この自己相関とは、元データと時間をずらしたデータとの相関の事で、前年度との相関を求める事で、未来の遷移を予測する事が出来ます。
例えば、2000年から2010年までの日本の総人口のデータと、2年ずらして、2002年から2012年までの日本の総人口のデータの相関をラグ2の自己相関係数といい、これを求める事を自己相関分析と言います。
自己相関分析を用いた時系列データ分析
今回は、国勢調査による、2000年から2020年の日本人の総人口の推移のデータについて、自己相関分析を行っていきます。
データの個数をそろえる点に注意して、まずは実際に自分でやってみましょう!
応用問題
Excelファイル3ページ目を使って、2000年から2020年の日本人の総人口の推移のデータについて、ラグ1(1年ずらし)の自己相関係数を求めてみて、日本の総人口が2021年以降どうなっていくのかについて予測してみましょう!
ラグ1(1年ずらし)の自己相関係数なので、2000年から2019年までのデータと、2001年から2020年までのデータの相関係数を求めます。
まず、下の様に、2000年から2019年までのデータと、2001年から2020年までのデータを抜き出して並べます。
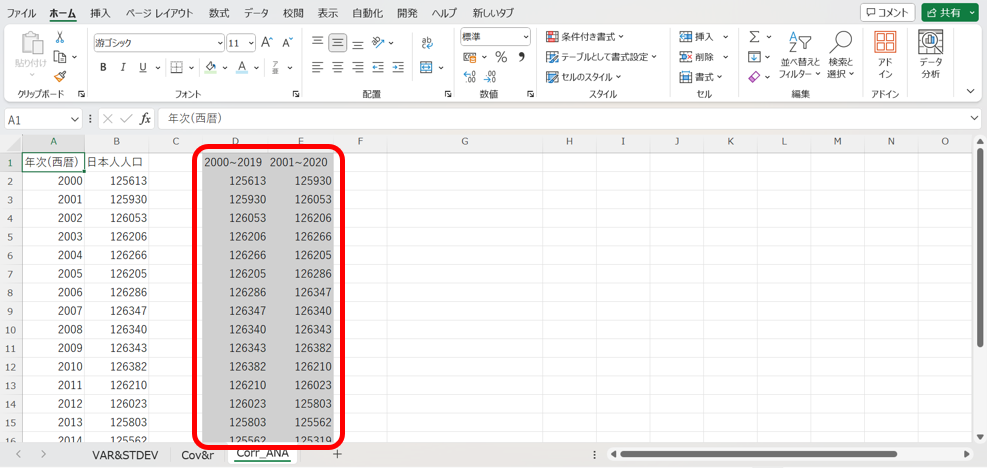
次に、下の様に、2つのデータについて、「関数」もしくは「データ分析ツール」を用いて相関係数を求めます。
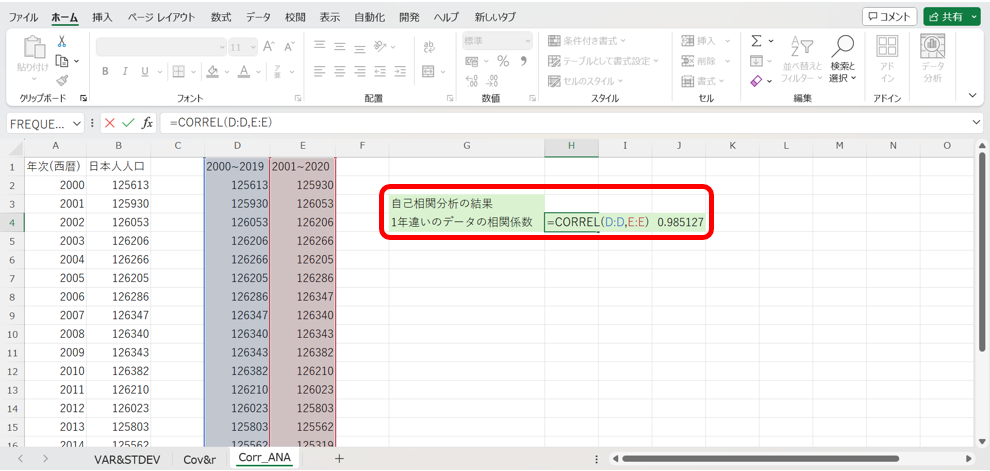
これより、2000年から2020年の日本人の総人口の推移のデータのラグ1の自己相関係数は約0.99である事が分かりました。
ある時点と1年後の時点の日本の総人口の関係が、おおよそ比例関係にあるという事は、前年度の人口が増えている時、来年度の人口も増える事が予想できます。
その為、2021年度以降の日本の総人口は増える、と数字で予測する事が出来ます。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
まとめ
今回のExcelによる統計解析講座第7章では、共分散と相関係数及び、そのExcelでの使い方について解説してきました。
今回から一気に統計分野の学習に足を踏み入れたこともあり、難しいと感じた方や、戸惑った方もいると思います。
しかし、今回から始まる統計分野の学習はデータ分析には不可欠で、非常に役立つ部分なので、理解出来るまで何回も読み直して欲しいです!
また、データ分析ツールに関しても、非常に便利な機能である為、設定して頂くのが良いと思います。
次章では、仮説検定に触れる前段階として、統計の基礎となる、確率分布、標本調査や、正規分布について学習していきます!
統計学及びデータ分析を学ぶ上で、避けては通れない道なので、是非読んでみて欲しいです!