excelはさまざまなデータを扱う際に有用なツールで、多くの場面で活躍しています。そしてそのデータの分析をexcelで行いたいけど、設定方法や分析の方法、結果の見方がよくわからない、と悩んだことはありませんか?
そこでこの記事では、データ分析を行いたいexcel初心者向けに、excelを使ったデータ分析の方法と結果の見方を図解します。excelでデータ分析を行い、その結果の判断を行う際の参考にしてください。
excelのデータ分析とは?
「excelのデータ分析」とは、データセットに対してさまざまなデータ分析を行うexcelの拡張機能のことです。
この機能を使用したデータ分析は、関数などを使わずにプルダウンメニューからデータ分析メニューを選択後、分析に必要な情報を入力するのみで比較的簡単に実行することができます。
初期状態では分析ツールは非表示
「excelのデータ分析」の機能はexcelの拡張機能であり、初期状態では表示されていないため、使用できるように設定する必要があります。設定については新たなダウンロードなどは不要で簡単に設定可能です。

分析ツールの導入方法
excelのデータ分析の機能を使用するための初期設定は、以下の手順で行います。
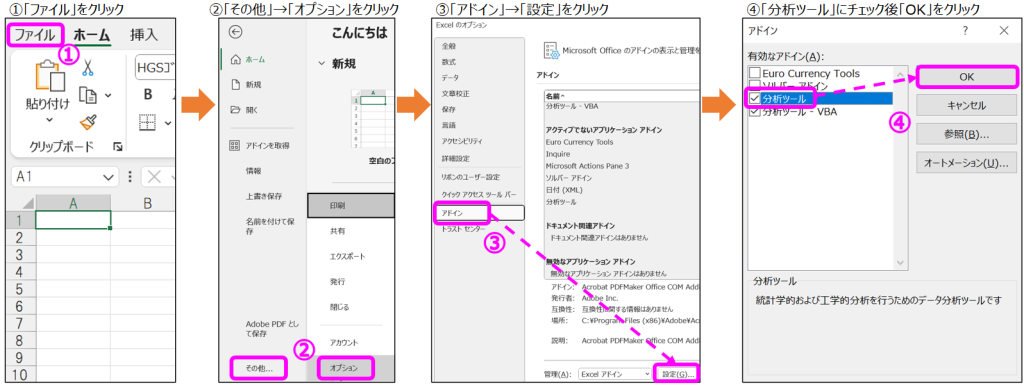
- excelを起動して「ファイル」タブをクリック
- 「その他」→「オプション」をクリック
- 開いた「Excelのオプション」ウィンドウの「アドイン」をクリック後、「設定」をクリック
- 開いた「アドイン」ウィンドウの「分析ツール」にチェックを入れて「OK」をクリック
初期設定は以上です。設定後「データ」タブの中に「データ分析」の項目が追加されます。

excelのデータ分析の種類
excelで準備されているデータ分析の種類は以下の19種類あります。
- 分散分析:一元配置
- 分散分析:繰り返しのある二元配置
- 分散分析:繰り返しのない二元配置
- 相関
- 共分散
- 基本統計量
- 指数平滑
- F検定:2標本を使った分散の検定
- フーリエ解析
- ヒストグラム
- 移動平均
- 乱数発生
- 順位と百分位数
- 回帰分析
- サンプリング
- t検定:一対の標本による平均の検定
- t検定:等分散を仮定した2標本による検定
- t検定:分散が等しくないと仮定した2標本による検定
- z検定:2標本による平均の検定
基本統計量や相関分析、回帰分析など、基本的な分析については対応しています。
ここでは、よく使用される代表的な分析手法7選について解説します。
①分散分析
分散分析とは、複数のグループ間で平均値に統計的に有意な差があるかどうかを判断するために使用される統計学の手法の1つです。
excelで準備されている分散分析は、以下の3種類があります。
- 「分散分析:一元配置」1つの要因を持つデータに対して行う分散分析
- 「分散分析:繰り返しのある二元配置」お互いに関連性のある2つの要因を持つデータに対して行う分散分析
- 「分散分析:繰り返しのない二元配置」お互いに独立している2つの要因を持つデータに対して行う分散分析
どういった目的でデータ分析を行うのかという用途によって使い分けます。
ここでは、「分散分析:一元配置」の実行例を図解します。
サンプルデータ:3つの製造プロセスの製品品質データ。各プロセス30個サンプリング。
①「データ」タブから「データ分析」をクリックし、データ分析ウィンドウから「分散解析:一元配置」を選択して「OK」をクリック。
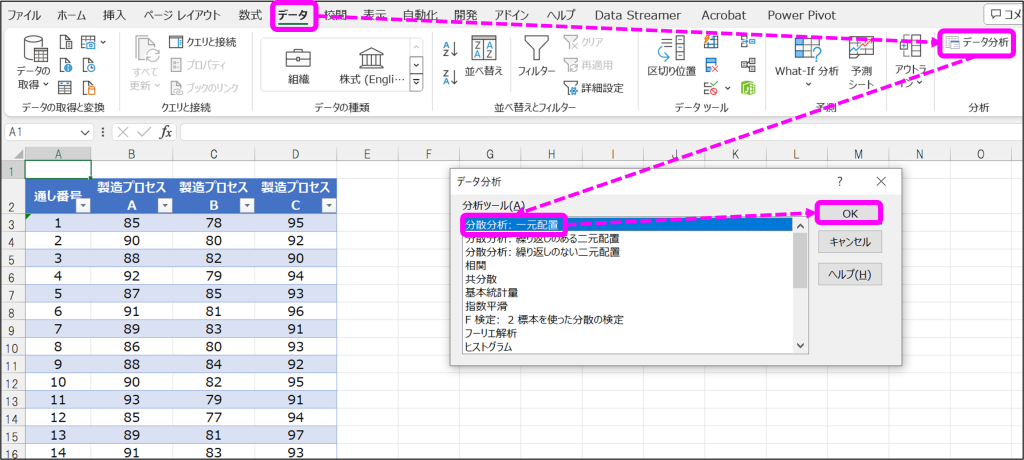
②分散分析のウィンドウで、入力範囲・データ方向、α(A)、出力先を指定して「OK」をクリック。
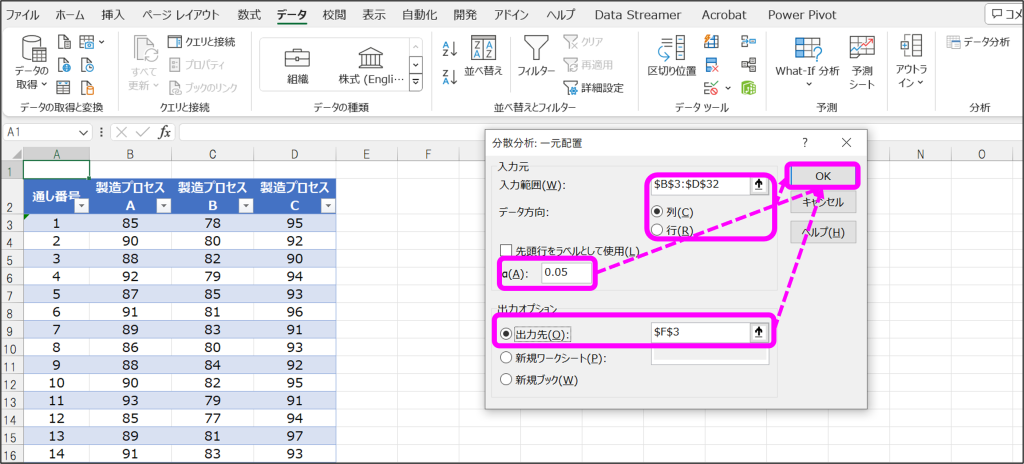
③指定した出力先に分析結果が出力。
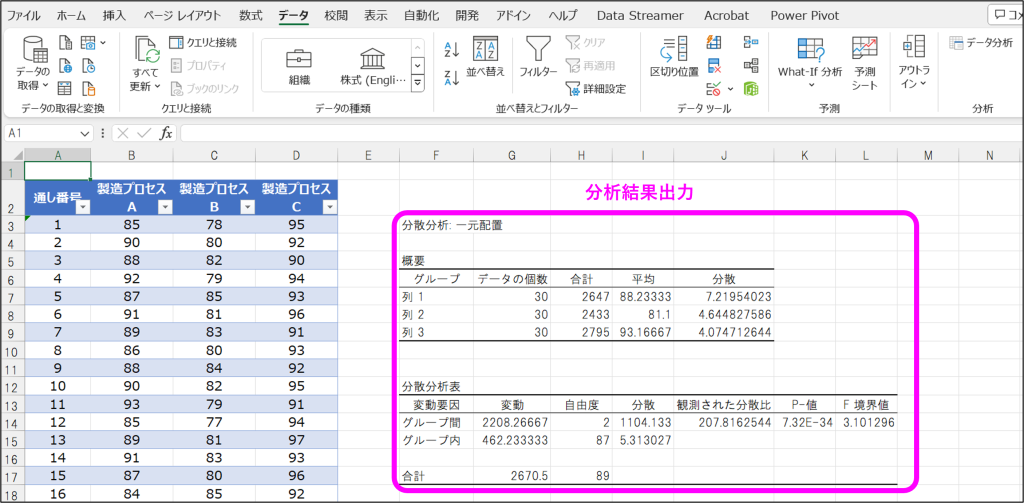
ここで着目するのは「P値」で、この値がα(A)より小さい場合、3つのデータセットの平均値に差があることを意味します。
この結果から、以下のようなことが分かります。
- P値がα(A)より小さいので、3つの製造プロセス間の品質の平均値に差がある。
②相関分析
相関分析とは、2つの変数間の関係性、つまり一方の変数が変化したときの他方の変数の変化の仕方に関係性があるか、を分析する手法です。
2つの変数間の関係性を表す指標を相関係数と呼び、ー1から1までの値をとります。
- 正の相関:相関係数が正の値をとる場合、正の相関関係にあります。この場合、一方の変数が増加すると他方の変数も増加し、逆も同様です。相関係数が1に近いほど変数間の関係性が強いことを意味します。
- 負の相関:相関係数が負の値をとる場合、負の相関関係にあります。この場合、一方の変数が増加すると他方の変数は減少し、逆も同様です。相関係数がー1に近いほど変数間の関係性が強いことを意味します。
- 無相関:相関係数が0に近い場合、変数間にはほとんど相関が無い、とみなされます。
相関関係・相関係数に関しては以下の記事で詳細に解説しています。

excelでの相関分析では相関係数で相関関係を表しますが、データ分析の機能以外で、各変数をそれぞれX軸、Y軸とした散布図を作成して視覚的に相関関係を確認することもよく行われます。
以下に実行例を図解します。
サンプルデータ:1か月間の最高気温および降水量と商品売上高の関係
①「データ」タブから「データ分析」をクリックし、データ分析ウィンドウから「相関」を選択して「OK」をクリック。
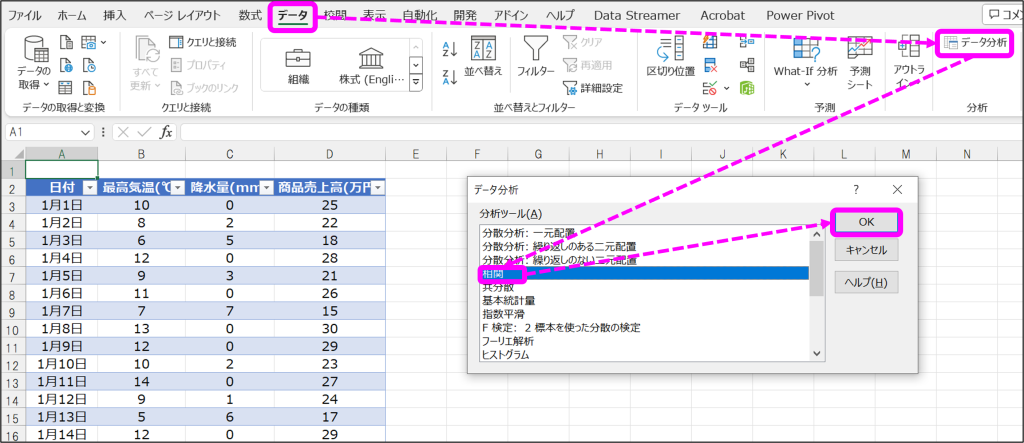
②相関のウィンドウで、入力範囲・データ方向、出力先を指定して「OK」をクリック。
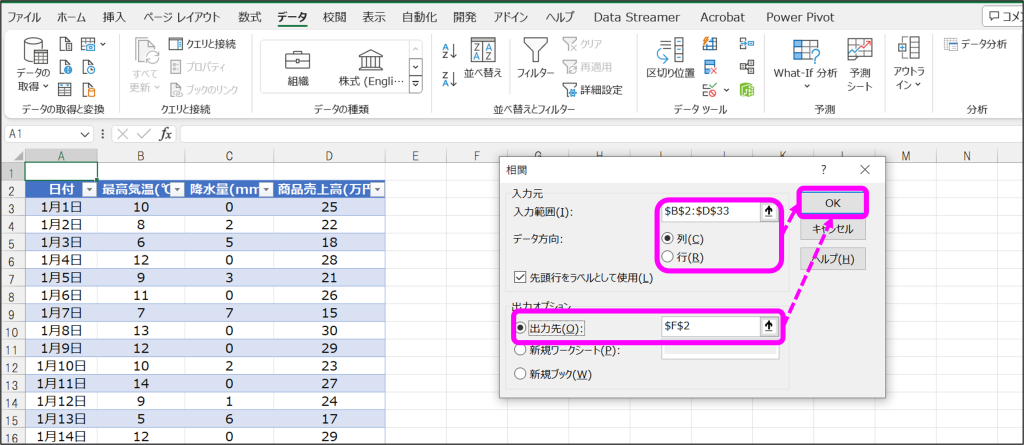
③指定した出力先に分析結果が出力。
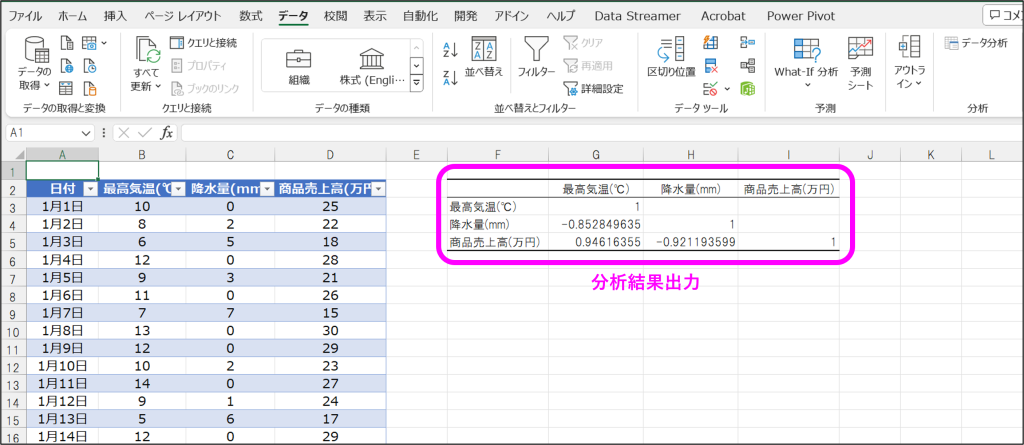
出力される分析結果はそれぞれの項目間の相関係数が表形式で出力されます。
この結果から、以下のようなことが分かります。
- 最高気温と商品売上高は正の相関があり、最高気温が高いほど商品売上高は増える。
- 降水量と商品売上高は負の相関があり、降水量が多いほど商品売上高は減る。
③基本統計量
基本統計量とは、データ全体にどのような特徴があるのかを数値で表して分析する手法です。
基本統計量には一般的に以下の指標を含みます。
- 平均:データ全ての合計をデータ数で割った数値
- 中央値:データを順番に並べた時の中央の数値
- 最頻値:データの中で最も頻度が高い数値
- 標準偏差:データのばらつき度合を表す数値
各基本統計量については以下の記事で詳細に解説しています。

以下に実行例を図解します。
サンプルデータ:店舗A、店舗Bの1ヶ月分の日毎の売上データ
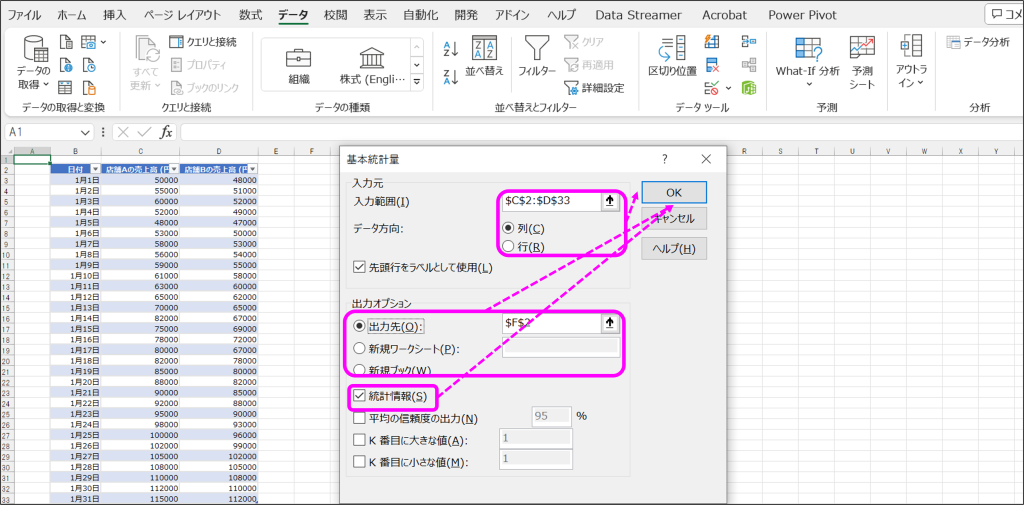
①「データ」タブから「データ分析」をクリックし、データ分析ウィンドウから「基本統計量」を選択して「OK」をクリック。
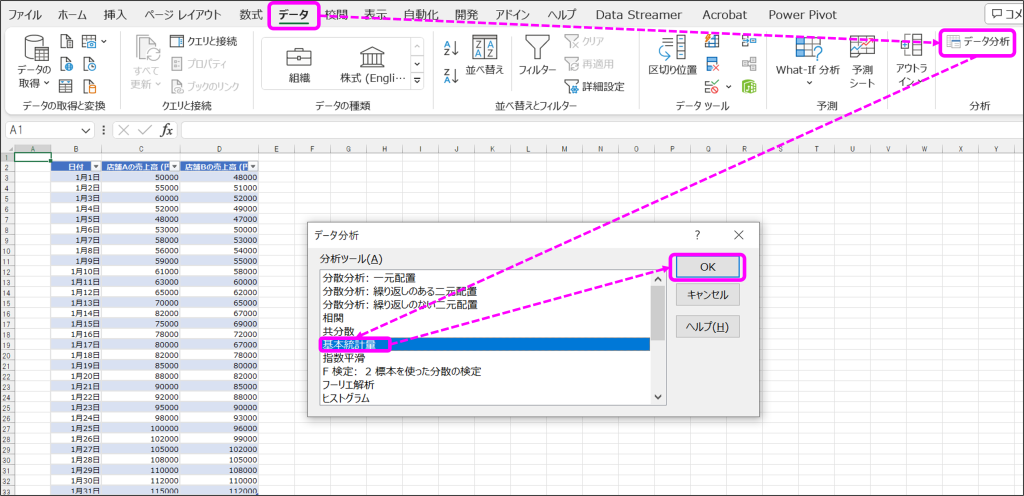
②基本統計量のウィンドウで、入力範囲・データ方向、出力先を指定して「統計情報」にチェックを入れて「OK」をクリック。
③指定した出力先に分析結果が出力。
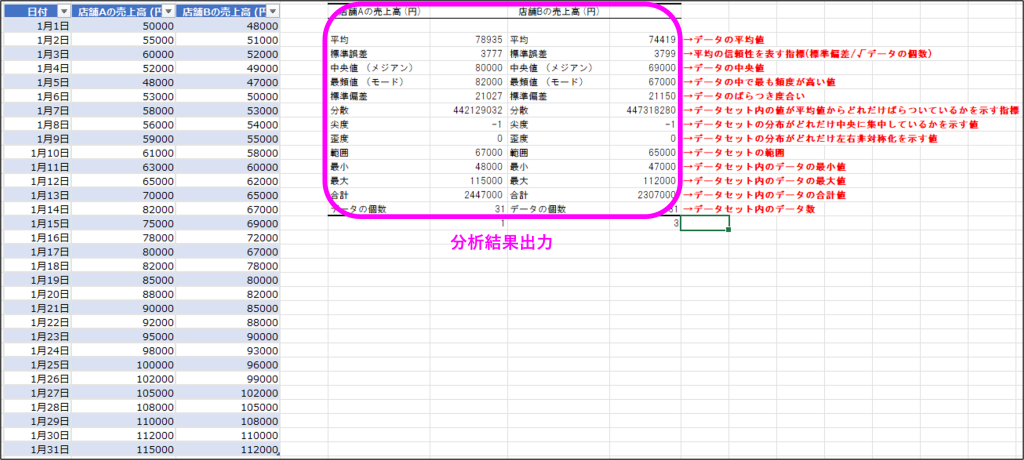
基本統計量の分析結果が出力されて、データ全体の特徴をとらえることができます。
この結果から、以下のようなことが分かります。
- 合計、平均から、店舗Aの方が店舗Bより売上は高い。
- 分散の大小から、店舗Bの方が店舗Aより日々の売上の変動が大きい。
④ヒストグラム
ヒストグラムとは、データをいくつかの区間(これを階級と呼びます)に分けて、それぞれの区間に含まれるデータの個数(これを度数と呼びます)を表す棒グラフでグラフ化したものです。(グラフ化せずに表形式でまとめたものを度数分布表と呼びます。)
ヒストグラムのメリットは、データ全体の傾向を視覚的に把握できること、データ中の異常値が発見できることが挙げられます。逆にデメリットは、決められた区間でデータをまとめるので、個々のデータが見えにくくなる点が挙げられます。
またヒストグラムの区間の幅を決める方法については、データ分析の目的によって異なりますが、5や10などの区切りの良い値、データの幅を区間の数で割って測定単位の整数倍に丸める、などの方法がとられます。
以下に実行例を図解します。
サンプルデータ:A組からE組までの計5クラス、各30人のテストの点数のデータ
①「データ」タブから「データ分析」をクリックし、データ分析ウィンドウから「ヒストグラム」を選択して「OK」をクリック。
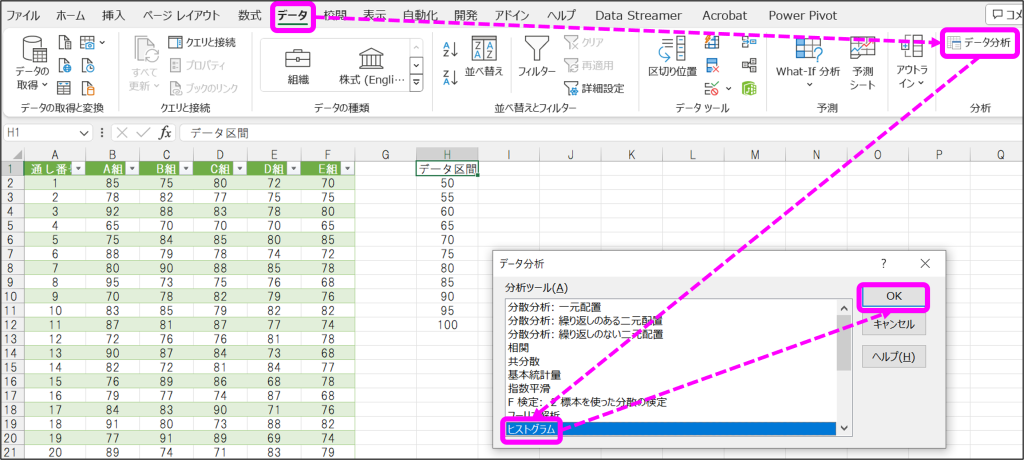
②ヒストグラムのウィンドウで、入力範囲、データ区間、出力先を指定して、「グラフ作成」にチェックを入れて「OK」をクリック。
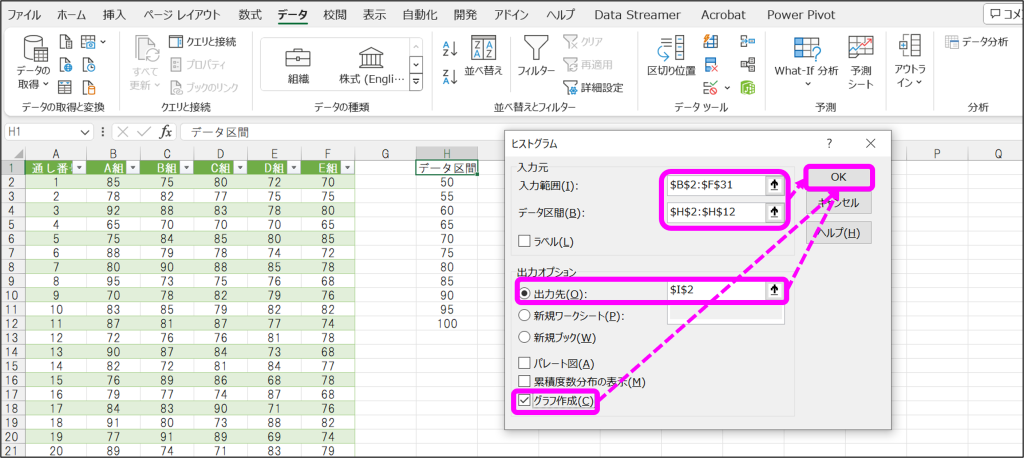
③指定した出力先に分析結果が出力。
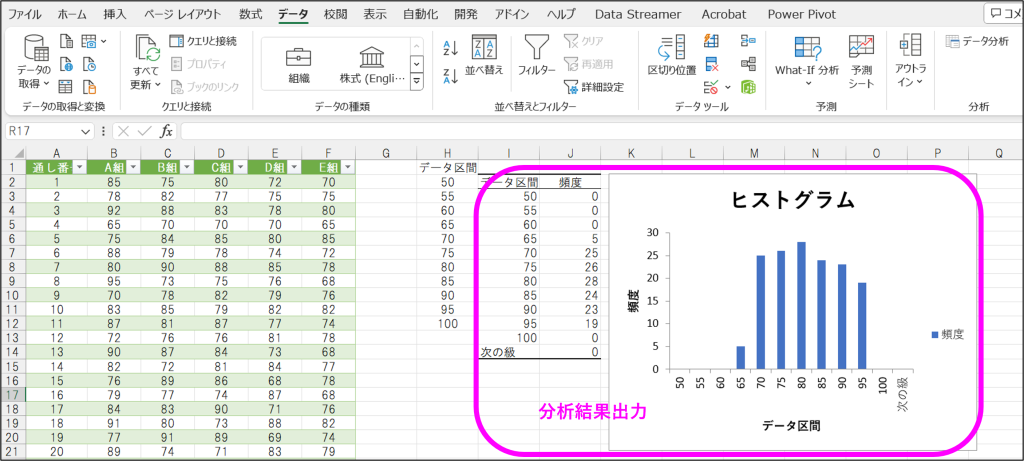
ヒストグラムの分析結果が出力されて、データ全体の傾向を視覚的に把握することができます。
この結果から、以下のようなことが分かります。
- 80点を中心に、プラスマイナス15点の間にまんべんなく分布している。
- 異常値(極端に低い点数)は無い。
⑤移動平均
移動平均とは、時系列データに対して一定の範囲ごとの平均値を、その範囲をずらしながら平均をとることで、データを平滑化する手法です。
移動平均は時系列データを分析する際に、データ全体の傾向を把握するために用いられます。
以下に実行例を図解します。
サンプルデータ:A社の株価の1か月間の推移のデータ
①「データ」タブから「データ分析」をクリックし、データ分析ウィンドウから「移動平均」を選択して「OK」をクリック。
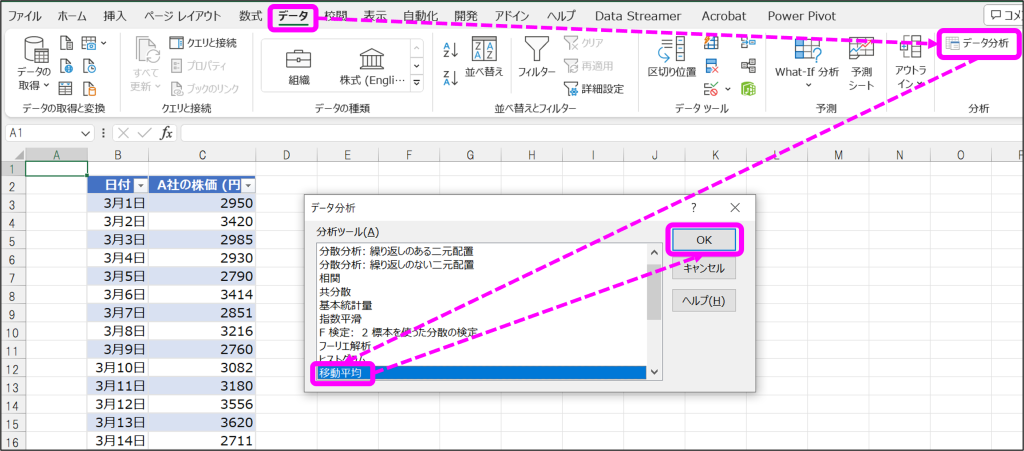
②移動平均のウィンドウで、入力範囲、区間、出力先を指定して、「グラフ作成」にチェックを入れて「OK」をクリック。
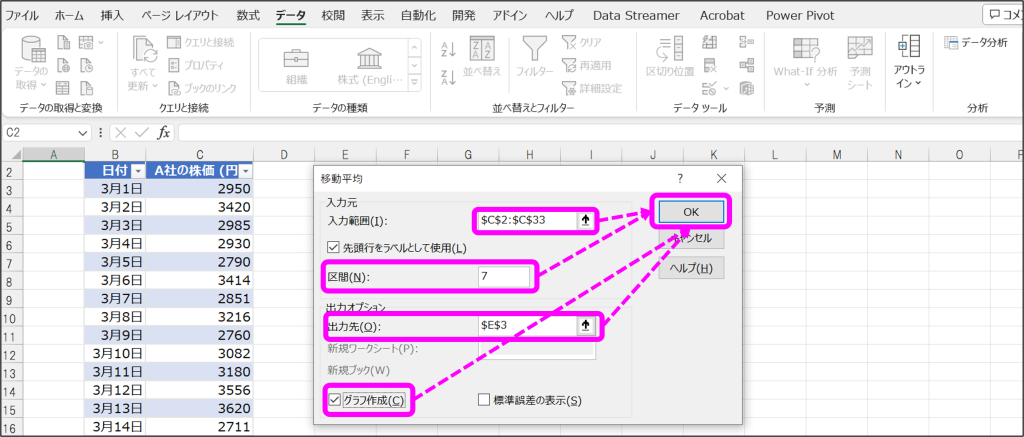
③指定した出力先に分析結果が出力。
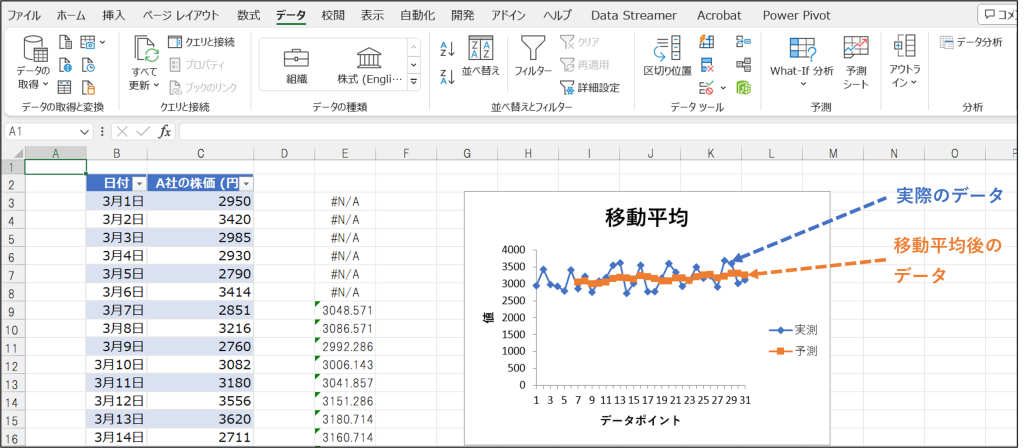
移動平均の分析結果が出力されて、実データのグラフより滑らかな移動平均線がプロットされています。
この結果から、以下のようなことが分かります。
- 移動平均線がほぼ平らであることから、A社の株価は安定傾向にある。
⑥回帰分析
回帰分析とは、ある変数(これを目的変数と呼びます)の変動に対して別の変数(これを説明変数と呼びます)の変動がどの程度影響を与えているかを分析する手法です。
回帰分析は目的変数に、より大きな影響を与えている説明変数がどれかを探す際に活用されます。
以下に実行例を図解します。
サンプルデータ:ある小売店の広告費と売上の関係
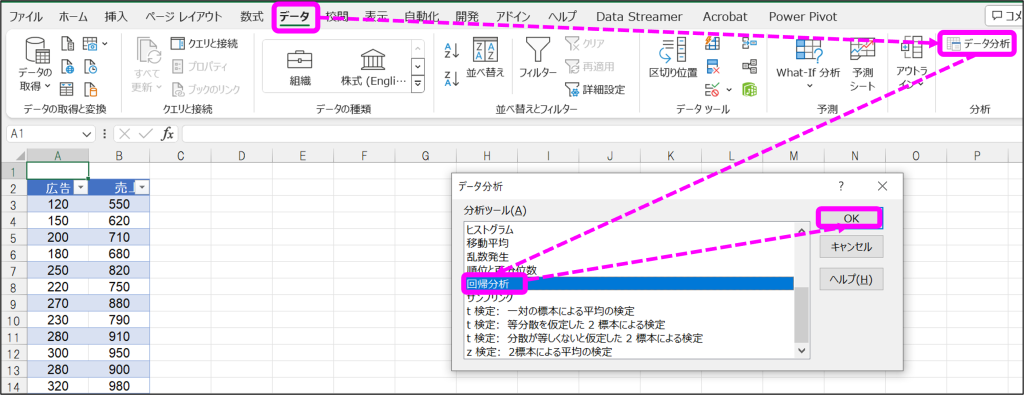
①「データ」タブから「データ分析」をクリックし、データ分析ウィンドウから「回帰分析」を選択して「OK」をクリック。
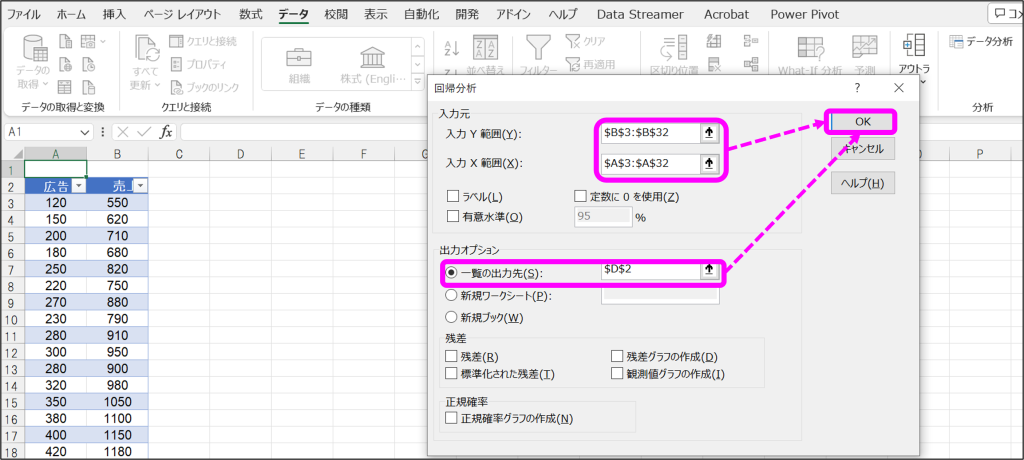
②回帰分析のウィンドウで、入力Y範囲、入力X範囲、一覧の出力先を指定して「OK」をクリック。
③指定した出力先に分析結果が出力。
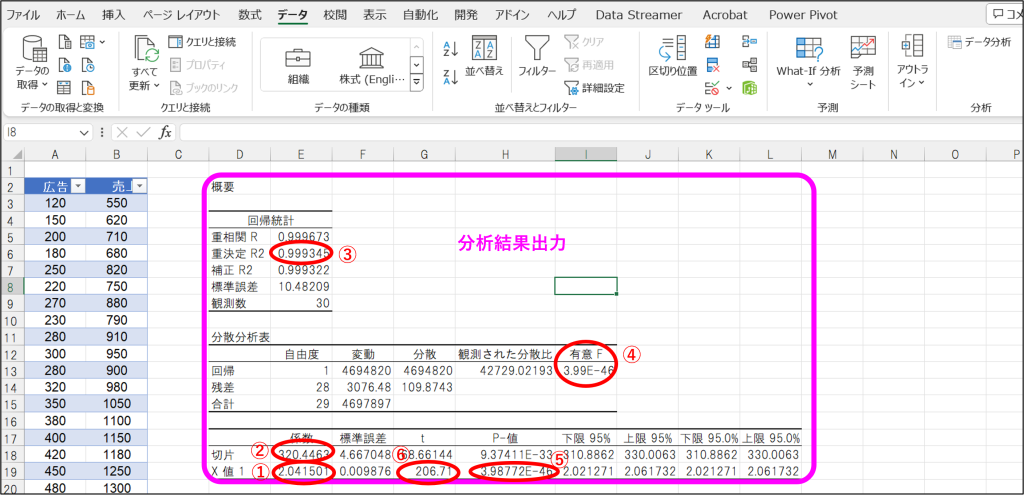
ここで分析結果出力について、代表的な単語を解説します。
| No | 項目 | 説明 |
| ① | 回帰係数 | 説明変数+1に対する目的変数の増減量 |
| ② | 切片 | 説明変数0の時の目的変数の値 |
| ③ | 重決定R2 | 得られた回帰式が目的変数の値変動をどの程度説明できているかを示す指標。0から1の値をとり、1に近いほど回帰式の精度が高いことを意味する。 |
| ④ | 有意F | 回帰式の有用性を示す指標。数値が小さいほど有用な回帰式であることを意味する。 |
| ⑤ | P値 | 個々の説明変数の目的変数に対する関係性を表す指標。一般的に0.05未満であれば関係性がある、と判断する。 単回帰分析では、④有意Fと同じ値。 |
| ⑥ | t値 | 説明変数が目的変数に与える影響の大きさを示す指標。t値の絶対値が大きいほど影響が強いことを意味する。 |
この結果から、以下のようなことが分かります。
- 「重決定R2」が1に近いので、得られた回帰式は精度が高い。
- t値が大きいので、広告費は売上に大きく影響する。
⑦t検定
t検定とは、2つのデータセットの平均に統計的な意味のある差(これを有意差と呼びます)があるかどうかを確認する分析手法です。
excelで準備されているt検定は、以下の3種類があります。
- 「t検定:一対の標本による平均の検定」:2つのデータセットが1対1で対応している場合
- 「t検定:等分散を仮定した2標本による検定」:2つのデータセットが異なる対象から抽出され、かつその2つのデータセットの分散が等しいと仮定する場合
- 「t検定:分散が等しくないと仮定した2標本による検定」:2つのデータセットが異なる対象から抽出され、かつその2つのデータセットの分散が等しいと仮定できない、もしくはわからない場合
どういった目的でt検定を行うのか、用途によって使い分けます。
ここでは、「t検定:分散が等しくないと仮定した2標本による検定」の実行例を図解します。
サンプルデータ:高血圧の治療を受けた人と受けていない人の各30人のデータ
①t検定の前段階として、F検定を行います。F検定とは、データセットの分散が等しいかどうかを検定する手法です。F検定の結果から、t検定で用いる手法を決定します。
「データ」タブから「データ分析」をクリックし、データ分析ウィンドウから「F検定:2標本を使った分散の検定」を選択して「OK」をクリック。
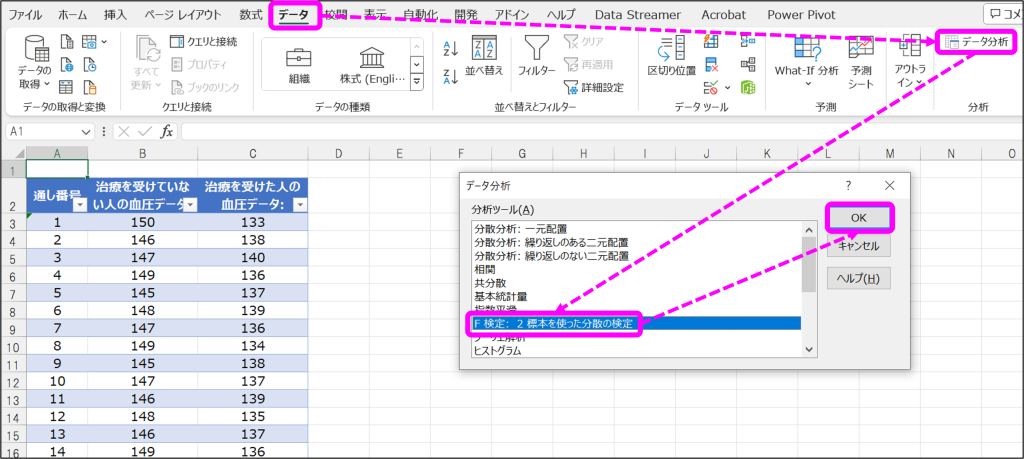
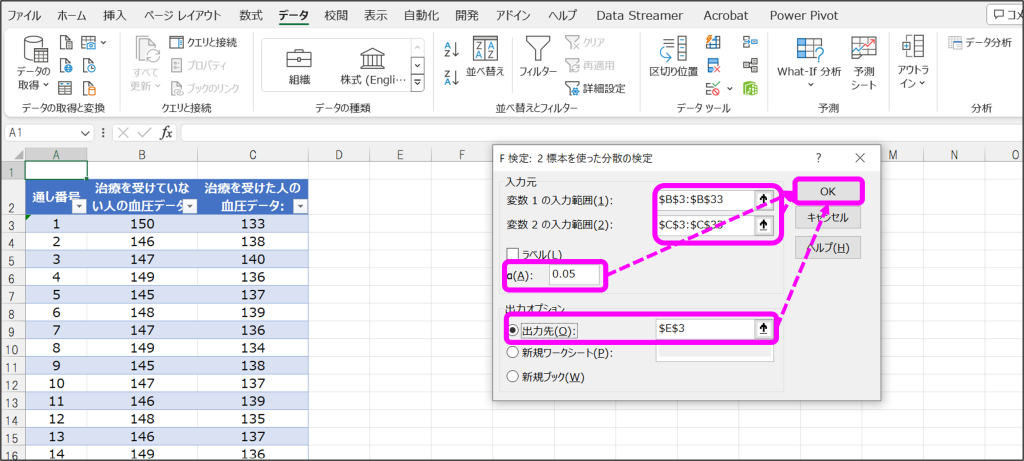
②F検定のウィンドウで、変数1の入力範囲、変数2の入力範囲、α(A)、出力先を指定して「OK」をクリック。ここで「α(A)」は、比較する分散が等しいかどうかを判定する閾値で、通常0.05や0.01が用いられます。
③指定した出力先に分析結果が出力。
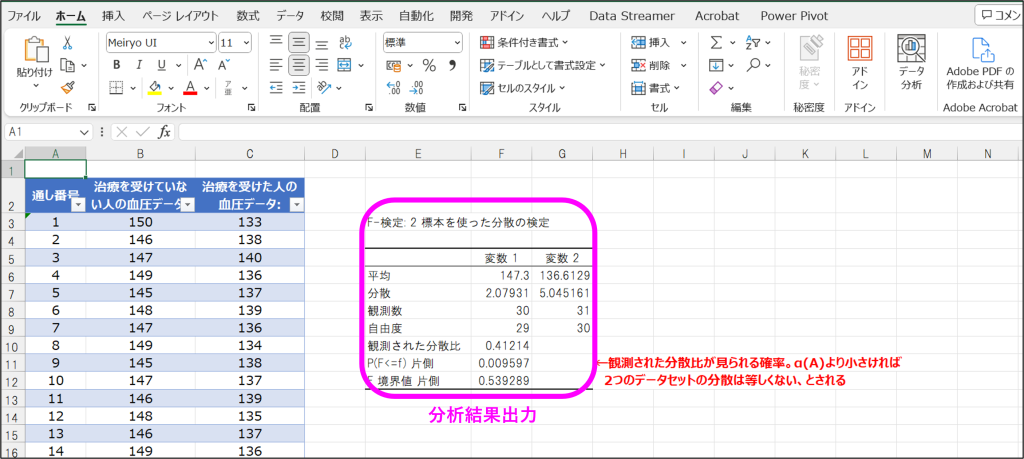
ここで2つのデータセットの分散が等しいかどうかの判定は、「P(F<=f)片側」の値が設定した「α(A)」との大小関係で行います。「P(F<=f)片側」が「α(A)」より小さい場合、2つのデータセットの分散は等しくない、ことを意味します。
今回の結果では、「P(F<=f)片側」が「α(A)」より小さいので、2つのデータセットの分散は等しくないことがわかり、t検定は「分散が等しくないと仮定した2標本による検定」で行います。
④「データ」タブから「データ分析」をクリックし、データ分析ウィンドウから「t検定:分散が等しくないと仮定した2標本による検定」を選択して「OK」をクリック。
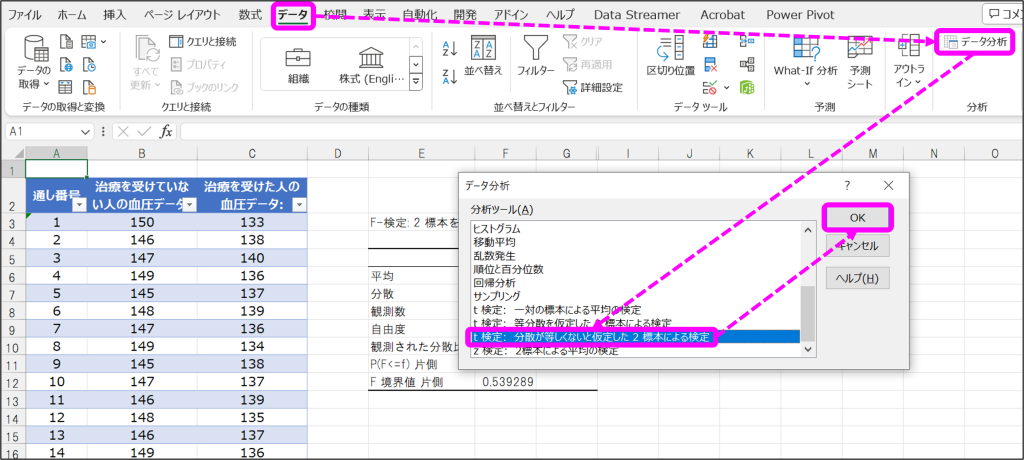
⑤t検定のウィンドウで、変数1の入力範囲、変数2の入力範囲、α(A)、出力先を指定して「OK」をクリック。
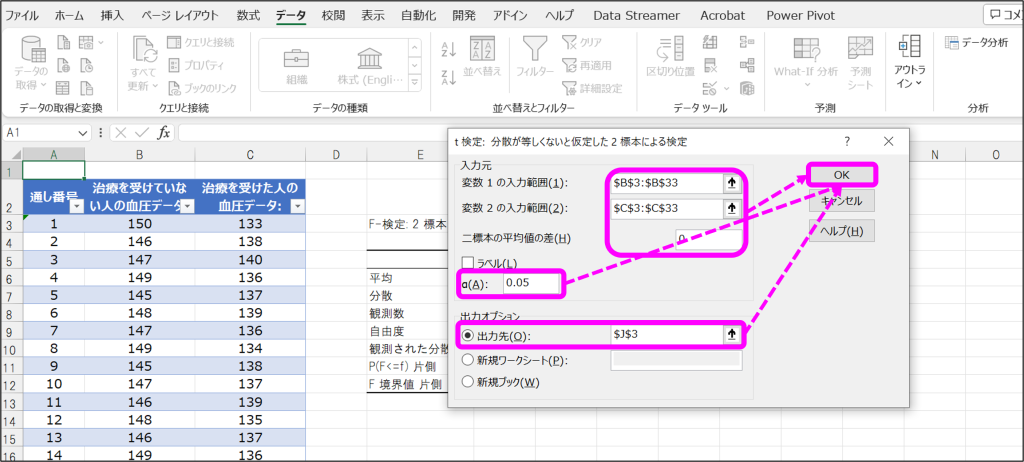
⑥指定した出力先に分析結果が出力。
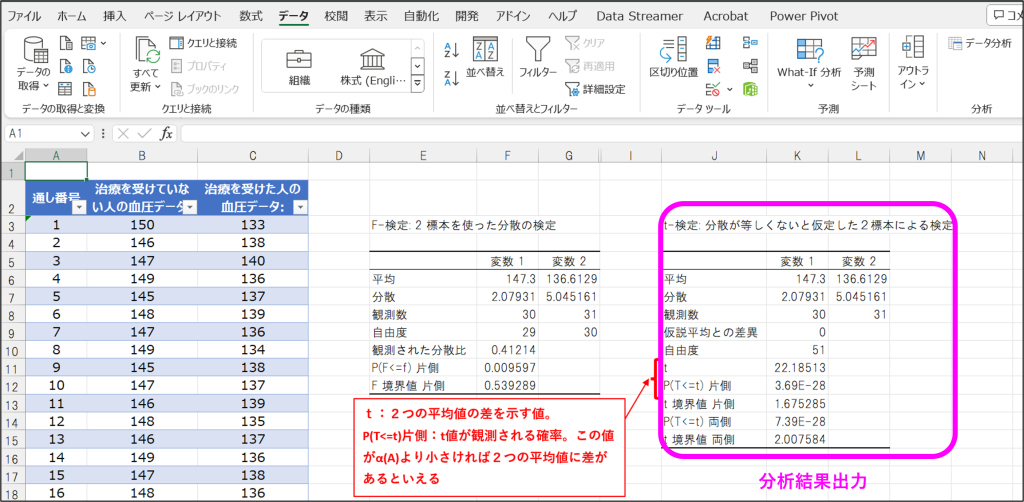
ここで「t」は2つのデータセットの平均値の差を示す値で、「P(T<=t)片側」はそのt値が観測される確率を示します。この「P(T<=t)片側」が「α(A)」よりも小さければ、2つの平均値に差がある、ことを意味します。
この結果から、以下のようなことが分かります。
- 「P(T<=t)片側」が「α(A)」よりも小さいので、2つの平均値には差がある。
excelを使ったデータ分析のトラブルシューティング例
excelを使ったデータ分析は比較的簡単にデータ分析が実行可能ですが、データに誤りがあったり、分析に必要な情報に入力ミスがあると、処理が実行できない場合があります。
そこでここでは、excelを使ったデータ分析のトラブルシューティング例を3つ紹介します。
①データのフォーマット不正
excelを使ったデータ分析では、データは数値である必要があります。数値以外の文字列などをデータに含めてしまうと、処理が実行できません。
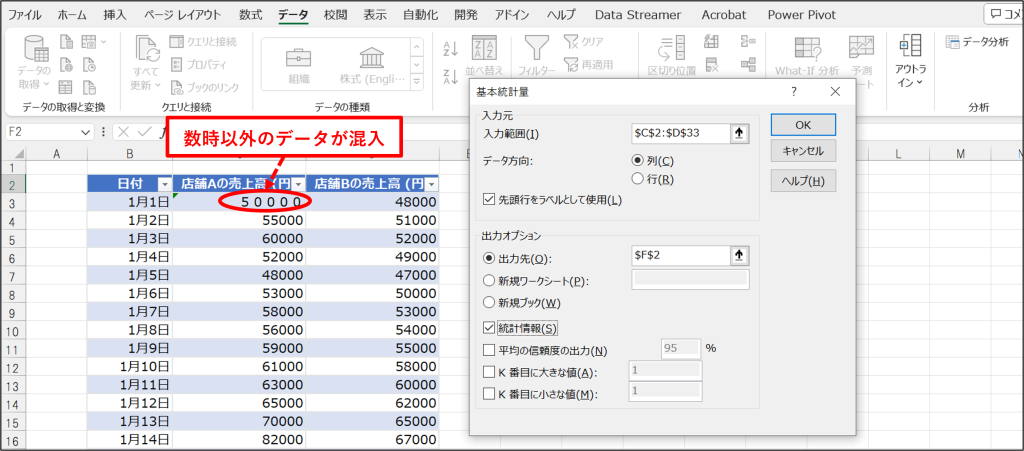
この例ではデータの中に「50000」という文字列が混入しています。この状態で分析を実行しようとすると、「入力範囲に数値以外のデータがあります」というメッセージが出て実行できません。
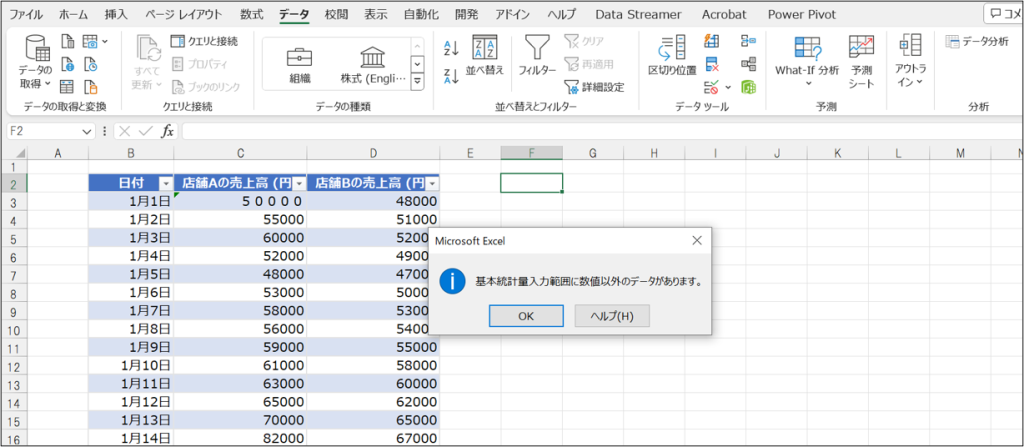
このような場合は、データ内の数値以外のデータを全て数値に修正して実行する必要があります。
②データ範囲不正
データ分析を行う際、データ範囲に制約がある項目があり、その制約に違反すると処理が実行できません。
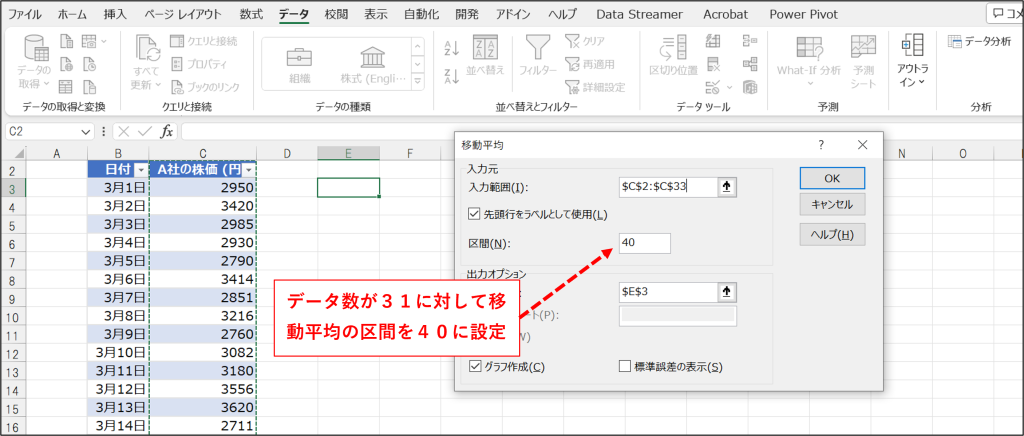
この例では、区間の指定はデータ数よりも小さい必要がありますが、データ数よりも大きい数値を区間に指定しています。この状態で分析を実行しようとすると、「移動平均区間はデータ件数より多くできません」というメッセージが出て実行できません。
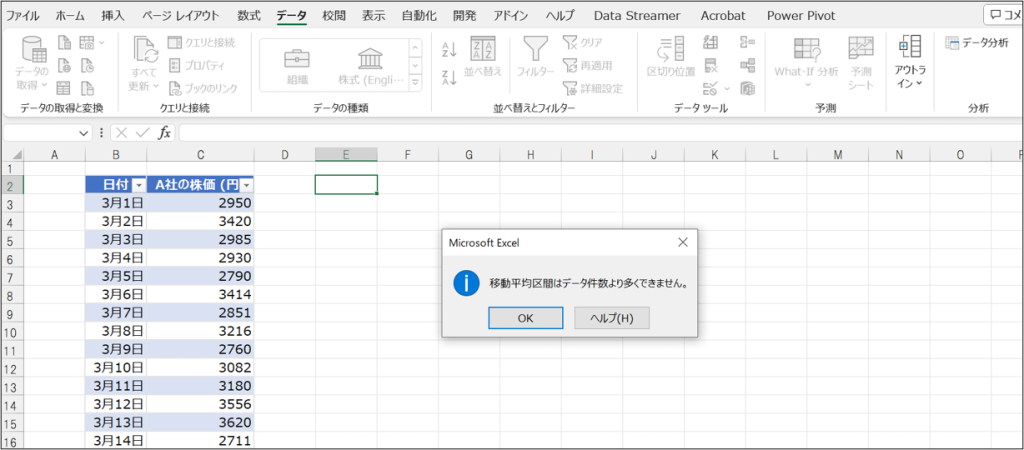
このような場合は、メッセージに記載の内容を修正して実行する必要があります。
③分析するデータ量過大
excelを使ったデータ分析はあくまでexcel上で実行するので、excelの制約である約100万行以上のデータは取り扱えません。
またexcelはパソコンで動作する以上、パソコンのスペックにも影響があります。データ量が多くても、データや分析条件に誤りが無ければ処理は投入されますが、パソコンのスペックによってはexcelが応答しなくなってしまいます。
そのような場合は、excelのフィルター機能などを使ってデータを間引いて処理を行うか、excel以外の方法でデータ分析を行う必要があります。

『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
excelを使った適切なデータ分析で仕事を一歩前へ
この記事ではデータ分析を行いたいexcel初心者向けに、excelを使ったデータ分析の方法と結果の見方を図解しました。
excelには拡張機能として、基本統計量や相関分析、回帰分析などの基本的な分析が19種類が準備されていて、複雑な計算式や関数を使用しなくても、分析に必要な情報を入力するのみで比較的簡単にデータ分析が実行可能です。
この便利な機能を使いこなして、仕事を一歩前へ進めましょう。