教師なし学習の勉強を進めると、階層的クラスタリングという用語が出てきます。階層的クラスタリングとはどのような手法なのでしょうか。
本記事では機械学習初心者の方向けに、階層的クラスタリングの概要、メリット、実装法を解説します。
階層的クラスタリングとは？
階層的クラスタリングとは、階層クラスター分析とも呼ばれ、似ているデータをまとめる手法です。教師なし学習の手法の一種で、人間が正解を与えずにデータだけを読み込ませて分析します。階層クラスタリングを通じて、クラスタ数をいくつに設定したらいいのか、また、どのデータ同士が似ているかが分析できます。
階層的クラスタリングで使われるデンドログラムとは？
階層的クラスタリングでは、デンドログラム（樹形図）が使用されます。
デンドログラムとは、どのデータが同一のクラスタに入っているのか、どのデータ同士が距離的に近いのかを表す図です。
以下ではとくにウォード法で考えた場合のデンドログラムで説明します。ウォード法の詳細は「階層的クラスタリングで使われる距離」をご覧ください。
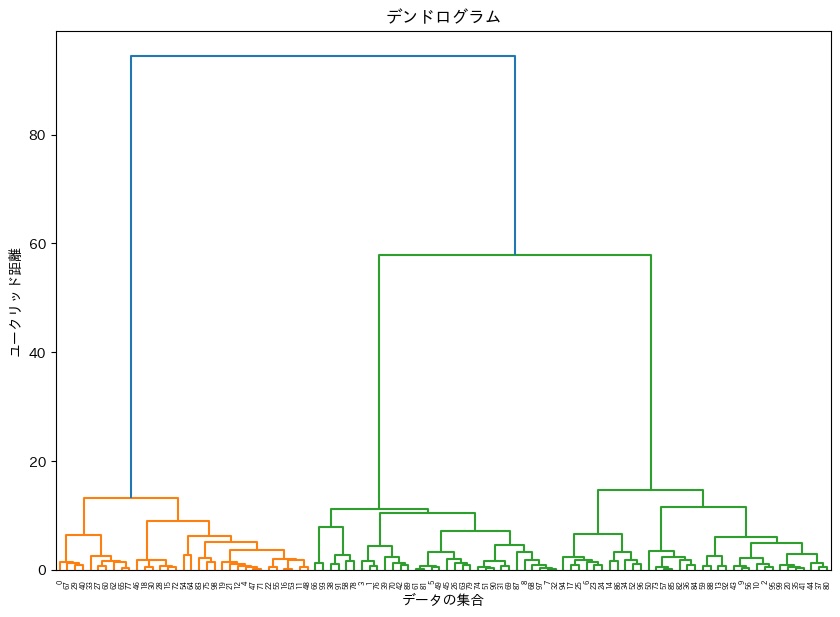
デンドログラムでは、階層クラスタリングの結果、下側から上側へとデータやクラスタ同士が統合されていく様子を表しています。
最も下側では、個別のデータをそれぞれ独立したクラスタとして考えます。その後、上に行くにしたがって、距離の近いクラスタ同士が統合されていきます。
このデンドログラムを作成することで、クラスタ数をいくつに設定すれば、データの背景にある事象をうまく説明できるかを分析できます。
上のデンドログラムの場合、クラスタ数を３つに設定すると最も満遍なくデータを分類できます。
階層的クラスタリングのメリットとデメリット
階層的クラスタリングのメリット
階層的クラスタリングのメリットは、クラスタ数を自由に設定できることです。k-means法のように、事前にクラスタ数を決める必要がないため、データの傾向が事前にわからない場合でも分析を進められます。
また、階層的クラスタリングの分析結果は、デンドログラムで表現されるので、視覚的にも理解がしやすいです。
階層的クラスタリングのデメリット
階層的クラスタリングはすべてのデータを計算するので、計算量が大きくなります。そのため、ビッグデータのような膨大な量をデータ分析する際は、階層的クラスタリングは不向きです。
階層的クラスタリングで使われる距離
階層的クラスタリングでは、2つのデータ間の距離やクラスタ間の距離が重要です。この２つの距離には複数の測定方法があります。
以下では、複数の測定方法のうち代表的なものを紹介します。
データ間の距離
２つのn次元のデータx、yの距離の測定には、以下の３つの距離が使用されます。
ユークリッド距離
ユークリッド距離は最も一般的な定義で、以下のように表されます。データ間を線分で結んだ際の長さがユークリッド距離に該当します。
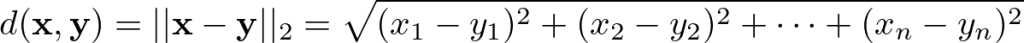
マンハッタン距離
マンハッタン距離は絶対値の和で定義された距離で、以下のように表されます。
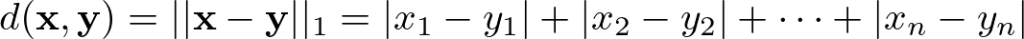
なお、ユークリッド距離とマンハッタン距離は以下のような関係があります。マンハッタン距離は直角三角形の底辺と高さの和、ユークリッド距離は直角三角形の斜辺の長さになります。
マハラノビス距離
マハラノビス距離はデータ間の相関関係を考慮した距離です。データのばらつきを考慮に入れた分析が可能です。
クラスタ間の距離
クラスタ間の距離には以下の４つの測定方法があります。
ウォード法
ウォード法は、最も近いデータ同士を１つのクラスタにまとめる、という処理を逐次行っていく手法です。
やや計算が煩雑ですが、データのばらつきの影響を受けづらいという特徴があります。
階層的クラスタリングで最も使用されている手法です。
群平均法
群平均法は、2つのクラスタそれぞれに含まれるデータ間のすべての組み合わせの距離を計算し、その距離の平均をクラスタ間の距離とする手法です。
最短距離法
最短距離法は、各クラスタのデータ間の距離のうち、最も距離が短いものをクラスタ間の距離とする手法です。計算が簡単ではありますが、外れ値に弱いという特徴があります。
重心法
重心法は、各クラスタで重心を取り、重心同士の距離をクラスタ間の距離とする手法です。計算が比較的簡単であるという特徴があります。
Pythonでの階層的クラスタリングの実装例
それでは、実際に、階層的クラスタリングをPythonで実装してみましょう。
階層的クラスタリングをPythonで実装する際は、SciPyというライブラリを利用します。
それでは、以下の図を階層的クラスタリングしてみましょう。
以下は、２つの特徴量を持つ100個のデータの集合です。
まず、実装に必要なライブラリをインストール、インポートします。
# japanize-matplotlibは作成する図の言語を日本語にする際に必要です。
pip install japanize-matplotlib
import japanize_matplotlib
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
from sklearn.metrics import silhouette_score次に、サンプルデータを生成します。
# サンプルデータの生成
# n_samplesはデータの数、centersはクラスタの数、cluster_stdはクラスタの標準偏差、random_stateでは乱数を固定しています。
# 本来、クラスタの数は事前にわかりませんが、視覚的にわかりやすくするために、設定しています。
data, true_labels = make_blobs(n_samples=100, centers=3, cluster_std=2.0, random_state=42)サンプルデータの生成後は、階層的クラスタリングを実施します。今回はウォード法を選択しました。
# 階層的クラスタリング
# methodを変えることで、その他の手法でも可能です。
linked = linkage(data, method='ward')階層的クラスタリングができたので、実際にデンドログラムを作成してみましょう。
# デンドログラムの表示
plt.figure(figsize=(10, 7))
dendrogram(linked)
plt.title('デンドログラム')
plt.xlabel('データの集合')
plt.ylabel('ユークリッド距離')
plt.show()このデンドログラムから、クラスタ数を３つにすると最もきれいにクラスタリングできることが予想されます。
最後に、デンドログラムをもとにクラスタリング結果をプロットします。
# クラスタの割り当て
# 最大のクラスタ数を設定します。
max_d = 15
clusters = fcluster(linked, max_d, criterion='distance')
# クラスタリング結果のプロット
plt.scatter(data[:, 0], data[:, 1], c=clusters, cmap='rainbow')
plt.title('階層的クラスタリングの結果')
plt.xlabel('特徴量1')
plt.ylabel('特徴量2')
plt.show()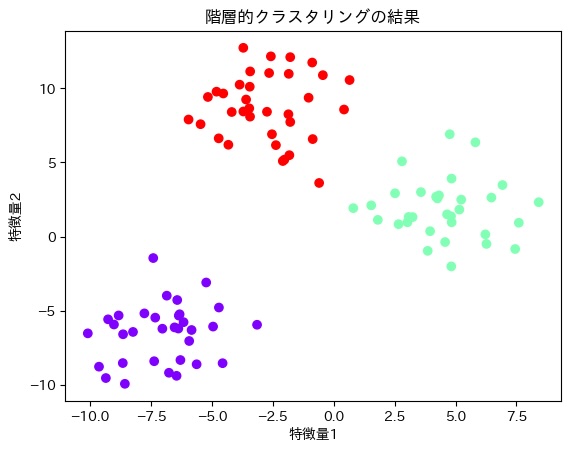
階層的クラスタリングの結果、上の図のような結果になりました。
以上のことから、今回のデータの集合のクラスタ数は３つにすると最もきれいに分類できることがわかりました。
まとめ
階層的クラスタリングは教師なし学習の一種で、データの集合を似ているもの同士でクラスタにまとめていく手法です。
階層的クラスタリングはクラスタ数を自由に設定できる、また、分析結果がデンドログラムで表されるので、視覚的にわかりやすいというメリットがあります。一方、すべてのデータを計算する必要があるので、計算量は大きくなります。
階層的クラスタリングはデータ間の距離やクラスタ間の距離によって、複数の手法があるので適切に使い分ける必要があります。
皆さんも、階層的クラスタリングを利用して、データの背後にある未知の傾向をつかめるようになりましょう。
https://www.tech-teacher.jp/blog/market/
参考文献
菅由紀子等「最短突破データサイエンティスト検定（リテラシーレベル）公式リファレンスブック 第2版」技術評論社 2022
参考URL
https://chokkan.github.io/mlnote/unsupervised/02hac.html
https://bellcurve.jp/statistics/course/27193.html
https://datawokagaku.com/hierarchical_clustering/
