ロジスティック回帰を聞いたことはありますか？
オッズ比やロジット変換といろいろな単語が出てくるけどいったい何？
結局何をやっているの？
と思っている人も多いのではないでしょうか。今回はロジスティック回帰についてわかりやすく解説していきたいと思います。
ロジスティック回帰とは
ロジスティック回帰は、統計学や機械学習の分野で広く使用される分類モデルです。特に二クラス分類で使われ、「合格/不合格」「陽性/陰性」などの予測に利用されます。
今回はロジスティック回帰の理論や内容について確認していきます。Pythonでの実装や実際の使用に関しては以下の記事で解説していますので、この記事で内容を確認したのちに以下の記事を参考に実際に分類を実施していただければと思います。
ロジスティック回帰の目的
ロジスティック回帰の出力
ロジスティック回帰は入力される説明変数からその事象が起こる可能性が出力され、それをもとにニクラスに分類していきます。
ロジスティック回帰を使用するメリット
ロジスティック回帰はその特徴より、以下のようなメリットがあります。
- 実装が容易：scikit-learnなどでモデルが準備されており、簡単に実装が可能です。
- モデルが単純：単純なモデルのため実装が簡単でありその割に精度が高く、解釈しやすい特徴があります。
- 線形モデル：ロジスティック回帰は線形モデルを用いて解析するため、説明変数と目的変数の関係を線形性をもって解析することが可能です。
- 出力が確率：Pythonで実装すると分類された結果に目が行きがちですが、本来分類結果は確率で出力されています。そのため、不確実性の検証や閾値の設定などが容易に行えます。
- 過学習の心配が少ない：線形モデルを算出する方法で分類しているため、比較的過学習が起こりにくいモデルになります。
- 重回帰分析：重回帰分析を行っているため、回帰変数を求めることにより各説明変数が与える影響が理解しやすくなります。
ロジスティック回帰の概要
ロジスティック回帰の算出方法の概要をここで見ていきます。その後、細かい内容を確認していきたいと思います。
結局何をしているの？
ロジスティック回帰は正誤判定を線形回帰で行い、正誤判定を確率で出力するためにシグモイド関数でロジスティック変換をして推定します。
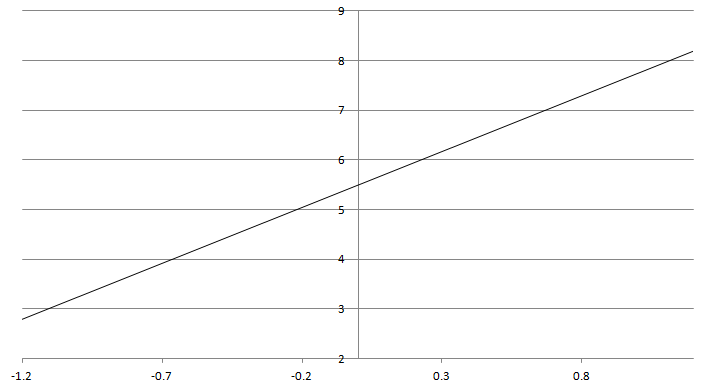
推定の式は、複数の説明変数から正答率を計算する重回帰分析を行います。一般の重回帰分析の式として、
- y = b1*x1 + b2*x2 + ・・・ + c
として算出します。
このように線形で推定された出力は際限なく数値が大きくなったり小さくなったりできるため、確率として0～1で出力できるようにロジスティック変換を行い、0～1で出力します。
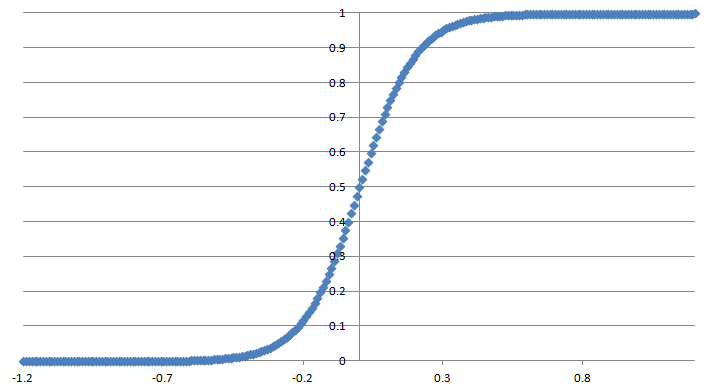
ロジスティック回帰の詳細
では、具体的にどのように回帰式を出しているか確認しておきましょう。
オッズ比
まずはオッズについて確認します。オッズとは、ある事象が発生する確率をPと置くと、以下のように示すことが可能です。
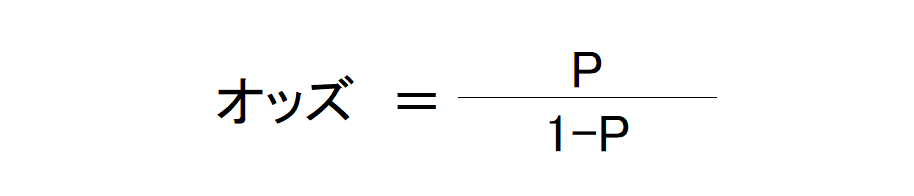
このオッズどうしの比率をオッズ比といいます。
ロジット変換
先ほど出したオッズですが、Pは確率なので０～１の値をとります。その際、Pが限りなく０に近づくとオッズは限りなく０に近づき、Pが限りなく１に近づくとオッズは際限なく大きな値をとることになります。
この問題を解決するために、これのLogをとります。そうすることにより、結果を0～1の間に収めることが可能です。この逆関数をとると、
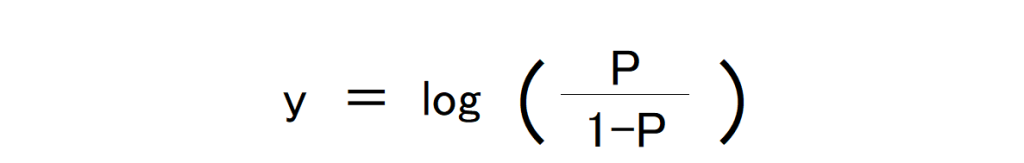
となり、
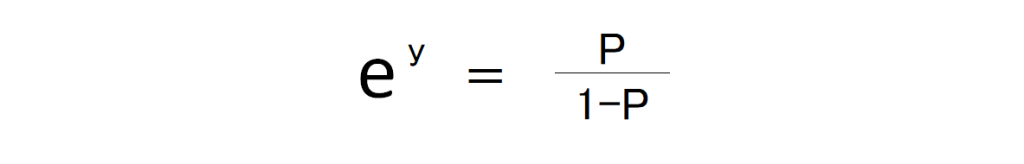
からｙを計算すると、
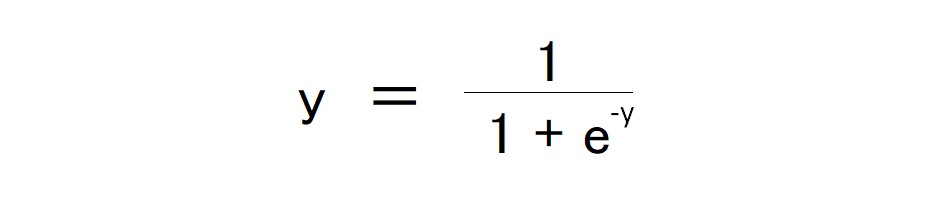
これをロジスティック関数、もしくはシグモイド関数とよび、これが上の項目で出てくるロジスティック変換の内容です。
重回帰分析の導入
ここから編回帰係数を最尤推定で求めます。尤度Lは以下のように算出可能です。
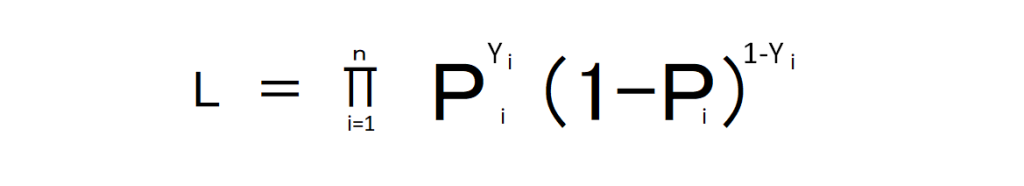
これの対数をとり先ほどのロジスティック関数に代入し、
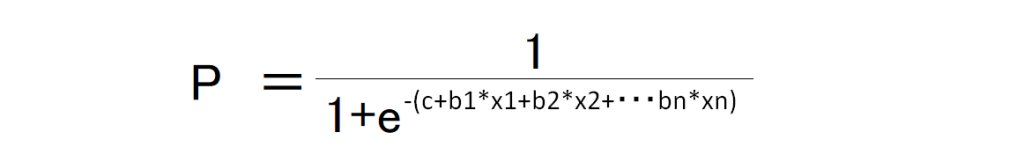
この式が導出されてきます。
重回帰分析と確率の算出
では、実際に確率を算出する方法を見てみましょう。
繰り返しになりますが、Pythonでモデル作成からモデル学習、結果の確認まで行う一連の流れは別記事に示していますので、合わせて確認してください。
偏回帰係数の算出
確率の算出に際し求める重回帰式ですが、以下のようになります。
- y = b1*x1 + b2*x2 + ・・・ + c
いくつかの説明変数と目的変数から実際に計算することは可能ですが、計算のコストが膨大になるため、今回は「scikit-learn」を使用して編回帰式を算出したいと思います。
なお、今回は回帰式の算出に必要な部分のみ記述しますので、Pythonで実際にモデルの作成をしたりする流れは別記事にまとめていますので、そちらを参考にしてください。
今回の前提条件
今回はscikit-learnのirisデータセットを利用します。
irisデータセットは
- setosa：ヒオウギアヤメ
- versicolor：ブルーフラッグ
- virginica：アイリス・バージニカ
という３つのカテゴリーに分かれているデータが、
- sepal length (cm)：がくへんの長さ
- sepal width (cm)：がくへんの幅
- petal length (cm)：花びらの長さ
- petal width (cm)：花びらの幅
という４つの説明変数を持っています。
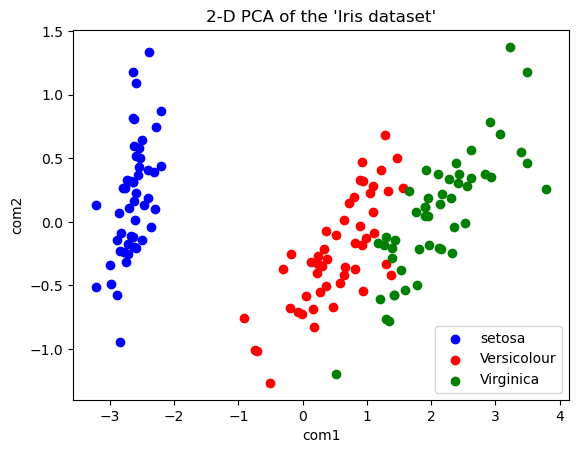
上の図は主成分分析を行ってirisデータセットのばらつきを見えるようにした図です。この中の青と赤、２つのクラスにしぼってロジスティック回帰で分析してみます。
主成分分析に関しては、以下の記事で扱っていますので、参考にしてください。
モデルの学習
先ほども書きましたが、機械学習でモデルを作成する方法は、誤差を最小にするところを探す、言い換えると「最も尤もらしい」ところを探す最尤推定を行っています。なので、厳密には統計的に重回帰式を解いているわけではありませんが、実用的にこの方法で全く問題はありません。
まず、scikit-learnのirisデータセットを読み込み、２クラスのみのデータにしたのちにトレーニングデータとテストデータに分割します。
その後、LogisticRegressionモデルを読み込んでモデルを学習します。
#必要なライブラリをインポートします。
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
#irisデータセットを読み込んでデータフレームにします。
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target'] = pd.DataFrame(iris.target, columns=['target'])
#２値分類にしたいので、カテゴリ２のデータを取り除きます。
df = df.query('target != 2')
#説明変数xと、目的変数yに分離し、80%をトレーニングデータ、20%をテストデータに振り分けます。
x = df[iris.feature_names]
y = df['target']
train_x, test_x, train_y, test_y = train_test_split(x, y, test_size=0.2, random_state=8)
display(train_x.head(), train_y.head(), test_x.head(), test_y.head())
#モデルを呼び出して学習を実施します。
model = LogisticRegression()
model.fit(train_x, train_y)回帰式の算出
LogisticRegressionを行うと、回帰式の各傾きと切片を出すことができます。
各回帰係数は「model.coef_」で確認できます。回帰係数が順番にarray形式で出力されます。
model.coef_
同様に切片は「model.intercept_」で確認できます。
model.intercept_
これらにより回帰式は
- y = 0.4047*x1 – 0.8350*x2 + 2.191*x3 + 0.881*x4 – 6.206
であることがわかりました。これに説明変数を入れ、ロジスティック関数に入れると確率が算出できます。
まとめ
今回はロジスティック回帰について確認してみました。ロジスティック回帰は通常使用する際はPythonで簡単に実装可能なため、何をしているかまで考えることはないかもしれません。
今回の内容を確認いただいて、ロジスティック回帰について理解を深めていただければと思います。
