機械学習を学び始めた方のなかには、下記のようなお悩みを抱えている方も多いのではないでしょうか?
- 損失関数って何?どうして必要なの?
- 損失関数の違いがわからない…
今回は、主要な損失関数を5つを紹介します。この記事の損失関数の数式と利用シーンの解説を通じて、プログラミングコードに落とし込む際に必要な知識を得られるでしょう。
損失関数を自分で実装したい方は、ぜひ最後までご覧くださいね。
損失関数の役割とは?
まずは、損失関数の役割について理解しておきましょう!
損失関数とは、機械学習モデルが予測した結果と正解との差を計算する数式のことです。ディープラーニングなどの教師あり学習の多くが、損失関数を最小化することで学習モデルを最適化させます。したがって、損失関数は学習精度を上げるうえで重要な役割を持ちます。
また機械学習を実行する側にとっても、損失関数は重要な指標です。損失関数の値を見れば、学習がうまくいっているか・失敗しているかがひと目で把握できるからです。ブラックボックスになる傾向がある機械学習の学習工程を理解するうえでも、損失関数は重要です。
【絶対押さえるべき】損失関数の種類と数式
さまざまな損失関数がありますが、どのような機械学習モデルにおいても「まずはこれを試すべき!」と言われている損失関数があります。機械学習を大きく回帰問題と分類問題に分けた場合に、それぞれで使われる頻度が高い損失関数は下記のとおりです。
- 回帰:平均二乗誤差
- 分類:交差エントロピー
この章では、平均二乗誤差と交差エントロピー誤差の数式と具体的な利用シーンを紹介します。両者は最低限押さえておくとよい損失関数なので、チェックしてみてくださいね!
平均二乗誤差

平均二乗誤差とは、それぞれのデータにおける正解値と予測値との差の二乗総和に対して、データ数で割って平均を計算する誤差関数です。
平均二乗誤差の特徴を把握するために、二乗差に当てはめて予測値の違いでどれくらい出力値に差が出てくるか見てみましょう。
条件:正解値が「5」のときに「3」もしくは「-2」と予測した場合
(5-3)^2=(2)^2=4
(5-(-2))^2=(7)^2=49
単純に差を求めるだけでも、-2の予測値の方が誤差が大きくなりますが、二乗を取ることでさらに誤差が大きくなっていることがわかります。
平均二乗誤差は、二次関数のグラフのように正解値から予測が外れるほど、機械学習モデルに対するペナルティを厳しく与えられるのです。正解値から大きく外れる値を過大に評価できることから、機械学習モデルからすると最適化すべき部分が明確なため、学習がスムーズに進みます。
また、平均二乗誤差は回帰問題におけるベンチマークや、平均的に優れた値を出せる機械学習モデルが欲しいケースでよく利用されます。
なお、機械学習の回帰問題の例は、下記の記事を参考にしてみてくださいね!

交差エントロピー誤差
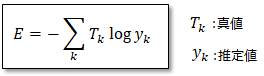
交差エントロピー誤差とは、正解値と予測値の自然対数との積を計算する誤差関数です。予測値が1未満の場合にはマイナスの値になることから、全体に対してマイナスを取らなければなりません。
交差エントロピーは分類問題に用いられ、正解値である「T_k」は実際のカテゴリーを1と0で表現します。例えばみかんとりんごの分類問題の場合に、みかんの画像に対しては(みかん,りんご)=(1,0)と表されるように、正解は「1」で不正解は「0」となります。
一方で、予測値である「Y_k」は(0 ~ 1)の確率分布です。例えば、みかんの画像に対して「正解はみかんっぽい」と予測する場合には(みかん,りんご)=(0.8,0.1)と出力するように、正解の見込み度合いに応じて確率が変わります。
また、エントロピーとは「分布の類似度を示す指標」のことで、正解と予測の分布が近ければ近いほどゼロに近づきます。
交差エントロピー誤差を具体的に理解するために、下記の条件で数式を見てみましょう。
条件:正解の確率分布が(1,0)のときに、予測した確率分布が(0.8,0.1)と(0.2,0.6)である場合
-(1×log(0.8)+0×log(0.1))=0.09
-(1×log(0.2)+0×log(0.6))=0.69
分類の正解値は「1と0」の確率分布で表現されるため、不正解値に対する予測値は相殺され、正解値に対する予測値のみが誤差として算出されます。
エントロピーの特徴と機械学習の分類問題における正解・不正解値の表現方法から、分類の誤差関数として広く利用されています。
また、交差エントロピー誤差は分類問題のなかでも、正解に対する予測値を厳しく評価したい場合に利用するケースが一般的です。
機械学習の分類問題について詳しく知りたい方は、下記をチェックしてくださいね!

【+α】損失関数の種類と数式
前述した平均二乗誤差と交差エントロピー誤差でうまく学習が進まない場合には、損失関数の試行錯誤が必要になります。
ここでは、試行錯誤を行うときの候補として検討すべき下記の損失関数を紹介します。
- 平均絶対誤差
- 平均二乗対数誤差
- Hinge損失
機械学習のモデルを少しでも向上させるために、それぞれチェックしておきましょう!
平均絶対誤差
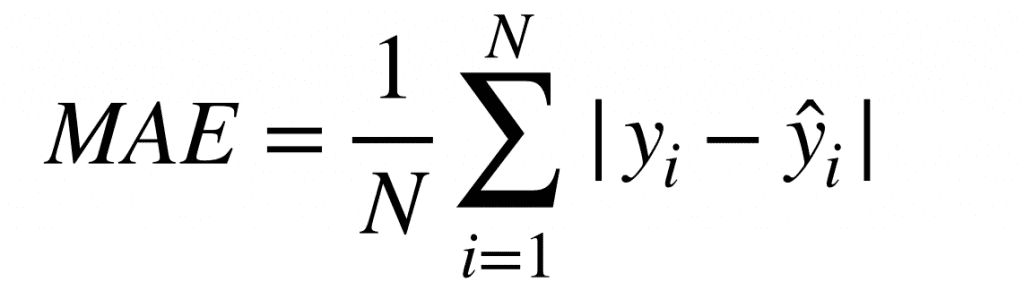
引用:【評価指標】MAEとは/AI Academy Media
平均絶対誤差とは、それぞれのデータにおける正解値と予測値との差の絶対値に対して、データ数で割って平均を計算する誤差関数です。
先述した平均二乗誤差と似ていますが、外れ値に対する評価の大きさが異なります。例えば、下記のように正解値と予測値の誤差が小さい場合には、平均二乗誤差と平均絶対誤差の評価値の差はほとんどありません。
条件:正解値が「5」のときに「3」と予測した場合
平均二乗誤差:(5-3)^2=(2)^2=4
平均絶対誤差:(5-3)=2
一方で、正解値に対する予測誤差が大きい場合は、下記のように大きく結果が異なります。
条件:正解値が「5」のときに「-2」と予測した場合
平均二乗誤差:(5-(-2))^2=(7)^2=49
平均絶対誤差:(5-(-2))=7
上記のように、平均絶対誤差の方が誤差間の分散が小さいことから、外れ値に対するペナルティを重要視しない場合には、平均絶対誤差の方が適しているといえます。平均絶対誤差は、外れ値の影響をなるべく無視したい回帰問題での利用が一般的です。
平均二乗対数誤差

引用:[損失関数/評価関数]平均二乗対数誤差(MSLE:Mean Squared Logarithmic Error)/RMSLE(MSLEの平方根)とは?/@IT
平均二乗対数誤差とは、正解値と予測値の差の二乗に対して自然対数を取り、データ数で割って平均を計算する誤差関数です。
平均二乗対数誤差は、対数関数のように小さい誤差に対しては小数点下記で繊細に評価するのに対して、正解値に対して大きく予測が外れても、大きなペナルティを与えないのが特徴です。
下記の例で、平均二乗対数誤差の誤差の特徴をチェックしておきましょう。
条件:正解値が「5」のときに「3」もしくは「4」と予測した場合
(log(1+4)-log(1+5))^2=(-0.07918)^2=0.006269
(log(1+3)-log(1+5))^2=(-0.1760)^2=0.03097
条件:正解値が「10000」のときに「3」と予測した場合
(log(1+3)-log(1+10000))^2=(-3.3979)^2=11.5457
平均二乗対数誤差の特徴から、株価の予測など微細に値を予測する回帰問題や、異常検知などで大きな異常値を排除できない回帰問題で使われています。
Hinge損失
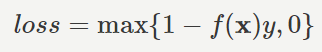
引用:ヒンジ損失/農学情報科学
Hinge損失とは、判別に成功しかつ境界から離れている・判別に成功したが境界線近く・判別に失敗の3つのケースで異なる値を出力する誤差関数です。具体的には、下記のように判別ケースごとで異なります。
- 判別に成功しかつ境界から離れている:0
- 判別に成功したが境界近く:1-f(x)y
- 判別に失敗:1-f(x)y
Hinge損失では、機械学習モデルを効率良く最適化するために、境界から離れた正解の確実性が高いものは誤差として含みません。
正しく判別できているものに対してはペナルティが緩く、判別できていないもの・失敗している可能性が高いものに対しては大きなペナルティを与えるのが特徴です。
また、Hinge損失はサポートベクターマシンを使う回帰・分類問題で頻繁に使われます。
Hinge損失の知識を深めるためには、SVMの理解が必要です。SVMの仕組みや実装例は、下記で詳しく解説しているので合わせてチェックしてくださいね!

損失関数と評価関数の違い
損失関数と評価関数は、適用するモデルの状態が異なります。損失関数とは機械学習モデルの最適化に使用する数式であるのに対して、評価関数は機械学習モデルの性能を測る数式です。
つまり、損失関数は学習中のモデルに対して使い、一方の評価関数は学習済みのモデルに対して適用します。
また、損失関数は評価関数としても使用するケースがあります。ただし、AUCやF値など評価関数として使用されている多くの数式が微分不可のものであるため、評価関数を損失関数として適用するケースはほとんどありません。
そのため、損失関数と評価関数を間違えると、機械学習モデルが正しく動かないケースがあるため混同しないように注意しましょう!
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
まとめ
機械学習の教師あり学習において、主要な損失関数は下記の5つです。
- 平均二乗誤差
- 交差エントロピー誤差
- 平均絶対誤差
- 平均二乗対数誤差
- Hinge損失
損失関数を最小化することで、機械学習モデルを最適化できます。そのため、それぞれ機械学習のケースに合わせて適切な損失関数を選ぶことで、格段に学習がうまく進むようになります。
今回紹介した内容をもっと深く知りたい方は、当社の「Tech Teacher」の利用がおすすめです!Tech Teacherでは、機械学習について熟知した教師からマンツーマンで指導を受けられます。興味や疑問がある方は、お気軽に「資料請求・無料体験」にお申込みください。