マルコフ決定過程は強化学習の基盤となる概念であり、「強化学習をしっかり理解したけど、難しい」と感じたことはありませんか?大学生、大学院生、エンジニアの方は強化学習の勉強や実装時に挫折しやすい内容なので、少しずつ読み進めてみましょう。
本記事では、最低限のポイントをまとめて、マルコフ決定過程の意味について理解しやすく解説します。
強化学習とは
機械学習は主に大きく以下の3種類での分類があります。
- 教師あり学習
- 教師なし学習
- 強化学習
教師あり学習は手書き数字の分類や認識といった入力データに対するラベルを判別するタスクで、教師なし学習は購入履歴から顧客をグループ分けするような入力データの関係性を見つけ出すタスクを担当します。
マルコフ決定過程は、3つ目の強化学習において用いられる統計学の確率過程です。強化学習では、人工知能が人と同じように囲碁や将棋をプレイし、勝ちやすい方法を自動的に見つけることができます。
基本的な強化学習の仕組みや活用例を知ってみましょう。
仕組み
強化学習で用いられる用語を5つご紹介します。
- エージェント(Agent)
- 行動(Action)
- 報酬(Reward)
- 環境(Environment)
- 状態(State)
強化学習は、エージェントが環境や状態から報酬を最大化する行動を選択できるように学習する分野です。エージェントは、学習するモデルのことで、環境と相互に影響を及ぼして学習を進め、最適な行動を選択します。
これは人と似た学習方法です。子供が自転車に乗れるように練習する過程を思い浮かべてください。自転車に乗るための練習過程で、子供はバランスを取るための様々な行動を試します。
最初は不安定で転びやすいかもしれませんが、繰り返しの試行と観察を通じて、バランスを取るための適切な行動を学ぶでしょう。転ぶことによる痛みを避けることができた経験から、自転車に乗るスキルを獲得していくのです。
活用例
2015年に囲碁の人工知能AlphaGoがプロの棋士を破り、世界中で話題となりました。実は、このモデルは強化学習を基盤としたニューラルネットワークが採用されており、戦術や戦略を繰り返し学習しています。
また、ロボティクス分野では自動運転車の制御や運転方針の最適化に強化学習が利用され、様々な状況での適切な判断が下せるように学習したモデルが活用されました。
金融の分野においても株価の予測や取引戦略の最適化研究のために強化学習が活用され、エージェントが市場の変動を理解できるように学習されます。
マルコフ決定過程とは
マルコフ決定過程(MDP, Markov Decision Process)は統計学における確率過程の一種です。確率過程は確率的な規則に従って変動する現象やシステムの数学的モデルを指します。そして、マルコフ決定過程は特に、未来の状態や報酬が現在の状態と現在の行動のみに依存するというマルコフ性を持つ確率過程です。
マルコフ性(Markov property)は、未来の状態や出来事が現在の状態や出来事のみに依存し、過去の履歴や情報には依存しないという性質を指します。
強化学習には用語が多いため、初めに概要を理解しておきましょう。
- エージェント Agent
強化学習の中心的な主体で、報酬を最大化する方策を学習し、状態と行動の組み合わせに応じて行動を選択する。 - 状態 State
システムや環境が取りうる特定の状態を表す。 - 行動 Action
エージェントが特定の状態で選択できる選択肢や行動のこと。 - 報酬 Reward
エージェントが特定の状態で特定の行動を実行したときに受ける即時のフィードバック。 - 遷移確率 Transition Probability
状態と行動の組み合わせが与えられたとき、次の状態がどれくらいの確率でどのように変わるかを示す確率分布。 - 方策 Policy
エージェントが特定の状態でどの行動を選択するかを規定する戦略や方針。 - 割引率 Discount Factor
将来の報酬を現在の価値として評価するために使用されるパラメータ。高い割引率は即時の報酬を重視し、低い割引率は将来の報酬を重視します。
強化学習はある状態においてエージェントが、報酬を最大化する行動を取るように学習が行われます。遠い将来に得られる報酬は割引率によっては価値の低いと判断されるため、パラメータの設定も重要です。
マルコフ決定過程の実装例
マルコフ決定過程がプログラムとしてどのように実装されるかを知るため、Q-Learningを用いた機械学習実装例をご紹介します。
Q-learningとは
Q学習(Q-learning)は強化学習のアルゴリズムの一つで、エージェントが未知の環境において最適な行動を学ぶための手法です。Q学習はマルコフ決定過程と呼ばれる数学的な枠組みに基づいています。
Q-learning概念は、ある状態と行動の組み合わせが、エージェントにとってどれだけ価値があるかを表す数値であるQ値(Q-value)を用いて、最適な行動を目指します。
Q学習の大まかな流れを見てみましょう。
- Q値をランダムに初期化
- 状態に基づいて行動を選択する
- 選んだ行動を実行し、環境から報酬を受け取る
- 現在のQ値や報酬、次の状態での最大Q値から、Q値を更新する
- 状態の更新: エージェントは次の状態に進み、次の行動の選択を行います。
- 収束と学習: 収束するまでQ-learningを繰り返し、最適なQ値が得られるまで学習が続けられます。
Q-learningは、エージェントが未知の環境で最適な行動を学び、制御するための非常に強力な手法であり、ロボティクス、ゲームプレイ、自動運転などのさまざまな応用分野で利用されています。

プログラム例
import numpy as np
import matplotlib.pyplot as plt
num_states = 5 # 状態空間の数
num_actions = 2 # 行動空間の数
learning_rate = 0.1 # 学習率
discount_factor = 0.9 # 割引率
epsilon = 0.1
Q = np.zeros((num_states, num_actions))
# 学習ループ
num_episodes = 1000
q_value_changes = []
for episode in range(num_episodes):
state = 0
old_q_values = np.copy(Q)
while state != num_states - 1:
if np.random.rand() < epsilon:
action = np.random.randint(num_actions)
else:
action = np.argmax(Q[state, :])
next_state = state + 1
reward = 1 if next_state == num_states - 1 else 0
Q[state, action] = (1 - learning_rate) * Q[state, action] + learning_rate * (reward + discount_factor * np.max(Q[next_state, :]))
state = next_state
q_value_changes.append(np.mean(np.abs(Q - old_q_values)))
# 結果の表示
plt.figure(figsize=(8, 6))
plt.plot(q_value_changes)
plt.xlabel("Episode")
plt.ylabel("Q-Value Change")
plt.tight_layout()
plt.show()このプログラムはシンプルなQ学習の実装例です。エピソード毎に繰り返される学習でε-greedy法に基づいた行動の選択で、探索による学習の停滞も改善されます。
ε-greedy法は、強化学習において探索と活用のバランスをとるための戦略で、エージェントはε(イプシロン)の確率でランダムな行動を選択(探索)し、1-εの確率で現在の最適な行動を選択します。
実行結果
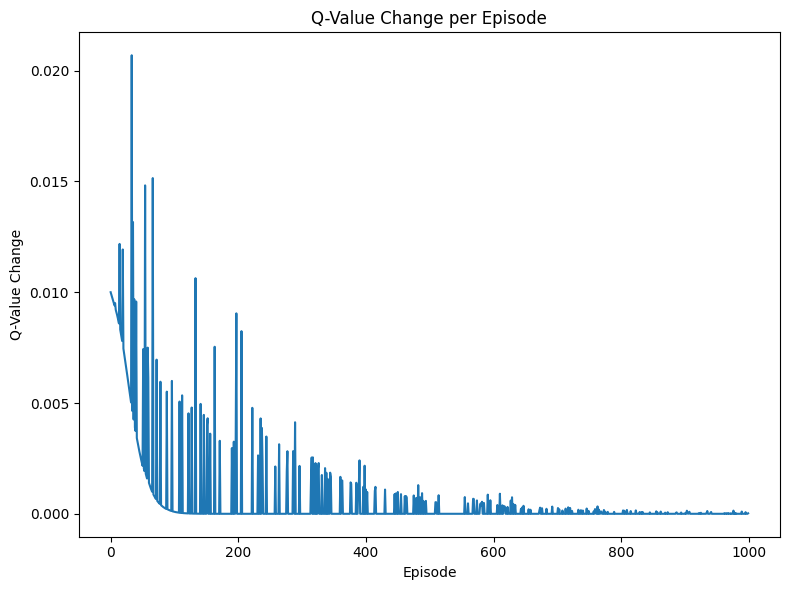
エピソードごとのQ値の変化をグラフにしたものです。徐々に変化が小さくなることが読み取れ、これは学習が収束に近づいたことを示しています。パラメータの設定次第では収束せずに処理が終わらない場合があるため、適度な探索を活用するように注意しましょう。
学習方法
数学
マルコフ決定過程では状態遷移の確率が与えられたとき、初期状態からどのよう変化するかに着目した確率過程です。確率過程は数学の確率論に関する専門用語で、離散時間型と連続時間型の2種類があります。
強化学習の実装を目的とする方は詳細な数式の変形や意味についての理解は必ずしも必要ありませんが、詳細に表記された数式を読み取れると、より鮮明なモデルの理解が可能です。
プログラミング
強化学習を含む機械学習は一般的にPythonで記述されます。Pythonには便利な処理をまとめたライブラリやコーディングの簡潔さが特徴として挙げられ、複雑な機械学習と相性の良いプログラミング言語です。
代表的な機械学習ライブラリにはPyTorchやTensorFlowなどがありますが、コードの簡潔さや拡張性の高さに違いがあるため、特徴に応じて最適なライブラリを利用しましょう。
機械学習
これまでに統計学に基づいた古典的な手法や生物の脳を模したニューラルネットのアルゴリズムが幅広く考案されてきました。強化学習はエージェントが環境に対して報酬を最大化する方法を学習します。
モデル構造の考案には統計学での計算やニューラルネットが用いられるため、幅広い機械学習のアルゴリズムに関する知識が強化学習を理解するのに効果的です。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
まとめ
マルコフ決定過程は強化学習の元となる数学的なモデルでしたが、理解するには基本的な用語の意味を知り、簡単なグリッドゲームなどで想像することが重要です。他の機械学習モデルと比べても複雑な数式を用いるため、ある程度は確率・統計の知識を学び、ライブラリの使い方を学んでみましょう。









