高次元のデータを分析することときに利用するのが主成分分析です。
主成分分析をすることで、高次元のデータを情報量をできるだけ損なうことなく、次元削減できます。
本記事では、主成分分析の概要、メリット、因子分析との違いをわかりやすく説明します。
主成分分析とは？
主成分分析（PCA: Principal Component Analysis）とは、高次元データをできるだけ情報を失わずに、その本質的な特徴を捉えるための手法です。
高次元のデータをそのまま２次元や３次元のグラフで描写することはできません。
しかし、主成分分析をすることで、高次元のデータでもデータの特徴を保ったままグラフ表示できます。
本来主成分分析は高次元のデータを対象にしていますが、以下では簡単のため、2次元データを主成分分析して1次元データにする例を見ていきます。
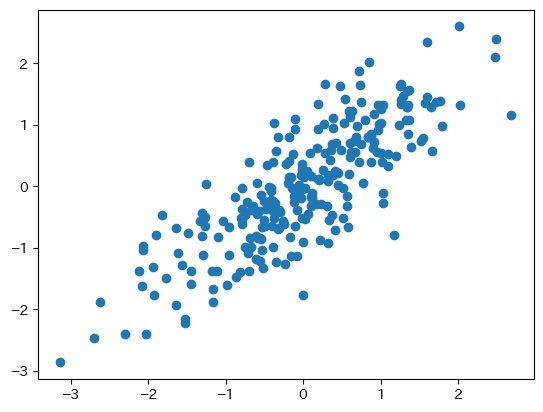
上の図は、とある２次元データのグラフです。
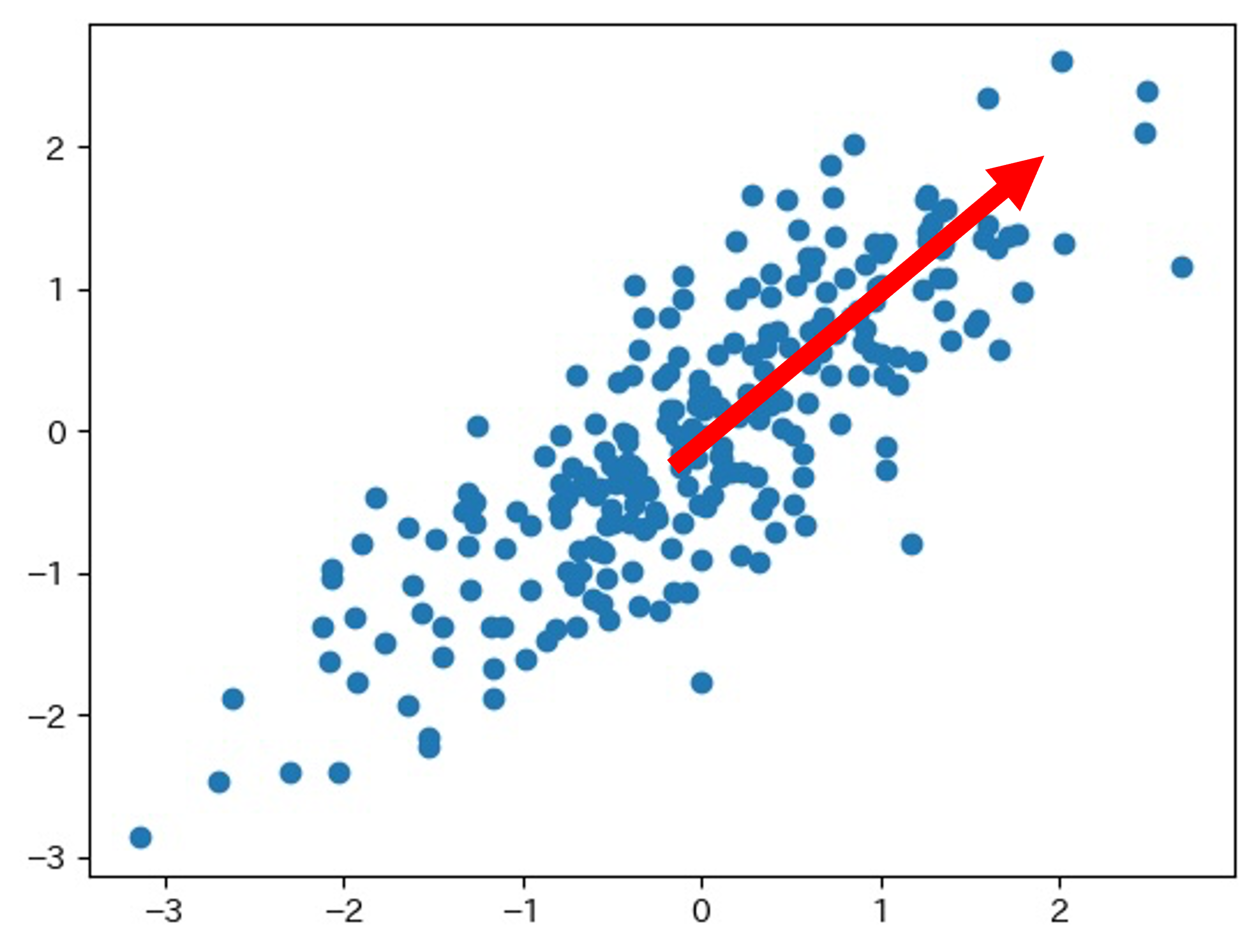
このグラフで、赤い矢印方向に新たに軸を設定し、この矢印方向に１次元データを作成します。
赤い矢印方向の１次元データはたしかにすべてのデータを説明できません。
しかし、この1次元データでも、データ全体の傾向を捉えられます。
このように、新たに設定する軸を「主成分」と言い、特に、最初に設定する主成分を「第1主成分」と言います。
第１主成分はデータの分散が最も大きい方向に設定されます。
情報量をさらに残したい場合は、第１主成分に加えて、第２主成分、第３主成分と順に設定していきます。
このように、主成分分析をすることで、高次元のデータを、できるだけその特徴を失わずにグラフ化できます。
主成分分析については以下の記事もご覧ください。
主成分分析のメリット
主成分分析の主なメリットは以下の３点です。
次元削減
主成分分析をすると次元を削減できます。
高次元のデータをそのままの状態で分析するには、データ量が多すぎてうまく分析できません。
主成分分析をすることで、データの情報量をできるだけ残しながら、データの次元を下げられます。
これにより、データを分析しやすくなります。
また、データの次元を下げると、分析に必要な計算量が小さくなるため、計算コストを下げられます。
次元削減についてもっと知りたい人は、以下の記事をご覧ください。
変数間の関係がわかる
主成分分析をすると、変数間がどのような関係にあるかがわかります。
高次元のデータは、そのままでは、それぞれの変数がどのような影響を与えているかがわかりづらいです。
主成分分析をすると、変数間の相関係数を求められらます。これによって、変数同士がどれだけ関係があるかを分析できるようになります。
データをグラフ化しやすくなる
主成分分析をすると、高次元のデータをグラフ化しやすくなります。
４次元以上のデータをそのまま私たちが普段利用する２次元や３次元のグラフで図示することは不可能です。
しかし、主成分分析から得られた主成分を用いることで、情報量をできるだけ減らすことなく、高次元のデータを２次元、または、３次元のグラフで表現できます。
グラフ化できると視覚的にデータが分析できるため、よりデータの理解を深められます。
主成分分析と因子分析の違いは？
主成分分析に似た概念として因子分析があります。
主成分分析と因子分析は、ともに変数の数を減らして、変換によって得られた新しい変数でデータを表現する手法です。
両者は、よく似た手法ですが、どのような違いがあるのでしょうか。
因子分析は、因子を事前に設定し、その因子がどれだけデータに寄与しているかを調べる手法です。
因子は自由に設定できるので、因子は自分が扱いやすい形に設定できます。一方、データを説明するために見当違いな因数を設定してしまうと、因子の寄与率が小さくなってしまい、分析の意味がなくなります。
主成分分析は、分析結果をもとに、主成分が決まります。データへの寄与率が高い主成分から順に決まっていくため、データを少ない変数で説明できます。しかし、分析によって得られた主成分の解釈は自分で行なければならず、また、その解釈自体が難しい場合もあります。
このように、主成分分析と因子分析は、新たに変換する変数を、事前に設定するか、分析結果をもとに設定するかという違いがあります。
どちらの分析をするにせよ、データがなぜそのような因子や主成分で説明できるかを解釈するには、そのデータの分野の深いドメイン知識が求められます。
主成分分析の利用例
主成分分析はさまざまな分野で利用されています。以下では、主成分分析が使われている例を３つ紹介します。
マーケティング
主成分分析を用いて、マーケティングの調査ができます。
顧客が、特定の商品を購入するかはさまざまな要因が複合的に関係してきます。例えば、年齢や性別、年収など顧客自身の特徴も関係してくるでしょう。また、商品のブランド、価格、色合い、質感など商品自身の特徴も深く関係しています。
このような、複数の要素があるものをそのまま分析するのは大変です。そのため、主成分分析をすることで、次元を削減しながら、どのような商品がより購入されやすいかを調査できます。
テストの結果の分析
テストの結果を主成分分析することで、より深く分析結果を解釈できるようになります。
例えば、とある中学校で国語、英語、数学、理科、社会の５教科のテストがあったとします。このテストの結果を主成分分析すると、国語の成績が良かった生徒は、他にどの教科の成績が良い傾向があるのか、また、どの教科の成績が悪くなる傾向があるのかなどの分析ができます。
画像処理
画像処理でも、主成分分析は利用されます。
画像は、大量のデータを含んでいるので、そのままの形では、計算コストがかかります。
そこで、主成分分析をすることで、画像の本質的な部分を残しながら、次元削減をします。これによって、画像処理に必要な計算量を減らせます。
主成分分析の実装例
最後に、実際にPythonで主成分分析の実例を示します。
まず、必要なライブラリをinstall、importします。
# グラフ内の言葉を日本語したい場合、installしましょう。
!pip install japanize-matplotlib# 必要なライブラリをimport
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import japanize_matplotlib
import matplotlib.ticker as ticker
import japanize_matplotlib次に、データを読み込みます。今回は、ランダムに生成したデータを主成分分析します。
# 今回はランダムに生成したデータを主成分分析します。
sample = np.random.RandomState(1)
#２つの乱数を生成し、グラフを作成します。
X = np.dot(sample.rand(2, 3), sample.randn(3, 250)).Tその後、読み込んだデータを前処理します。
# 標準化
sc = StandardScaler()
X_std = sc.fit_transform(X)これから主成分分析するグラフを図示すると、以下のとおりです。
plt.scatter(X_std[:, 0], X_std[:, 1])このデータを主成分分析します。
# 主成分分析
pca = PCA(n_components=2)
pca.fit(X_std)第１主成分、第２主成分の分散を計算した結果を出力してみます。
すると、第１主成分の分散は、1.82706576、第２主成分の分散は0.18096637になります。
このように、主成分の分散の値は後半にいくにつれ、小さくなります。
print('各主成分の分散:{}'.format(pca.explained_variance_))主成分分析の結果を矢印で表してみます。
# パラメータ設定
arrowprops=dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
# 矢印を描くための関数
def draw_vector(v0, v1):
plt.gca().annotate('', v1, v0, arrowprops=arrowprops)
# 元のデータをプロット
plt.scatter(X_std[:, 0], X_std[:, 1], alpha=0.2)
# 主成分分析の2軸を矢印で表示する
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ - v)
plt.axis('equal');
plt.title('主成分分析の結果')
plt.annotate("第１主成分", xy = (2, 1.5), fontsize=15)
plt.annotate("第2主成分", xy = (-2, 1), fontsize=15)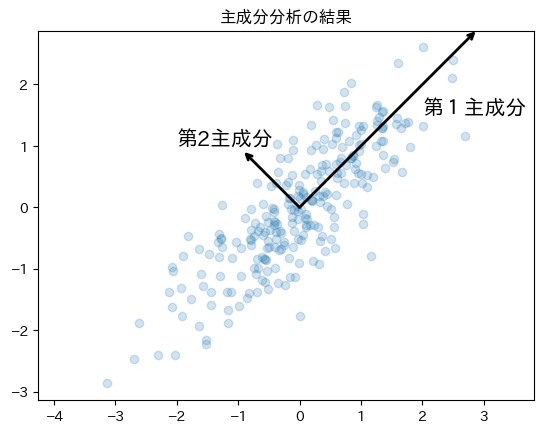
このグラフでは、左下から右上に伸びる方向が最も分散が大きいです。そのため、第１主成分は上の図の方向になります。
また、次の第２主成分は、第１主成分と直交するように設定します。そのため、第２主成分の軸は、第１主成分に直交しつつ、分散が最も大きくなる右下から左上に進む方向へ設定します。
最後に、累積寄与率を見てみましょう。
# 累積寄与率を図示する
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.xlabel("主成分")
plt.ylabel("累積寄与率")
plt.grid()
plt.show()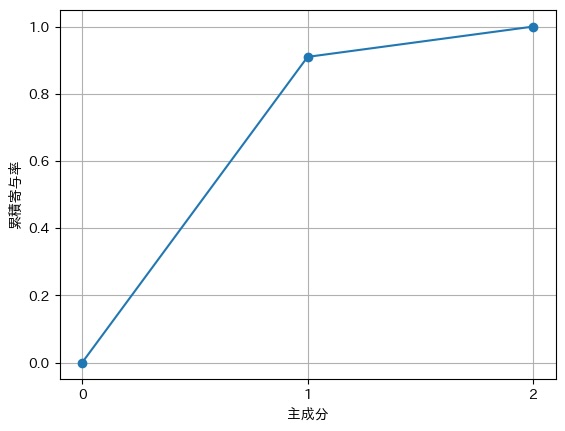
今回の場合、第１主成分の寄与率のみで、約９割あります。つまり、このデータは、第１主成分のみで、約９割を説明できていることになります。
まとめ
主成分分析は、情報量をできるだけ残しながら、高次元データの次元を削減するための手法です。
主成分分析をすることで、グラフ化しやすくなったり、変数間の関係が分析しやすくなったりします。
また、因子分析と主成分分析は、似たような概念ですが、新しく設定する変数を自分で設定するか、分析結果によって設定するかの違いがあります。
主成分分析は、高次元のデータを分析する際にとても有効な手法ですので、機会があれば、ぜひ利用してみてください。
参考文献：塚本邦尊・山田典一・大澤文孝『東京大学のデータサイエンティスト育成講座』マイナビ出版 2019
