主成分分析というワードは聞いたことがある方も多いと思いますが、
名前からして非常に難しそう
Pythonじゃないとできないの?
という疑問をお持ちの方もお見えだと思います。今回はエクセルで主成分分析をする方法を確認してみましょう。
今回は特にタイトル通り簡単にできることに主眼を置いてやり方を考えてみました。とはいえエクセルで主成分分析をすると一部統計の知識も必要になりますので、一連の手続きでわからないことやエラーが発生した際にはTech Teacherにぜひお問い合わせください!
主成分分析とは
主成分分析とは、情報をより多くの情報をもった新しい軸で表現することにより、
- 情報量の多い軸でデータを見直す
- 次元を削減して情報を理解しやすくする
- 次元を削減して計算量を削減する
などを行うことです。もしくはその軸を探し、その軸で元の情報を表示する分析法です。
具体的には下図のように横軸、縦軸で情報を見るより赤色軸をとったほうがより多くの情報を表現できそうなデータに対して新たな赤い軸を考えることです。
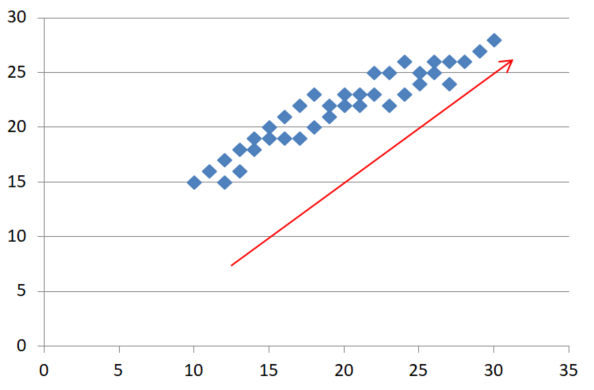
なお、主成分分析で「情報量が多い」とは、「その軸で多くの情報を持っている」=「その軸で多くのことを説明、分類ができる」ことであり、分散が多いことと同値といえます。
上の図で言うと元軸よりも赤い軸に対してのデータの分散が大きくなるため、この軸を探していくことになります。
この分散が最大となる軸を探し、それに対する直交軸の中で最大の分散を持つものを次の軸と、次々と軸を探していくことが主成分分析の作業となります。
次元削減をする際は変換後の軸であれば少ない軸で多くの情報を説明できるので、情報量の少ない軸を削除して少ない次元で元の情報を表現しようという考え方です。一般的には8割以上情報を残して軸を削除します。
今回はエクセルでこの新しい軸を探す方法を見ていきたいと思います。
主成分分析とPythonでの解法に関しては以下の記事でも取り扱っていますので、参考にしてください。

エクセルで主成分分析
今回はエクセルのみで主成分分析をしてみます。
事前準備
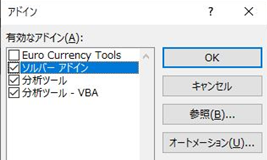
今回使用する機能「データ分析」と「ソルバー」は、初期状態では表示されていません。「データ」メニューの「分析」の中に、下記のように「データ分析」「ソルバー」が表示されていない場合は以下のように有効にしてください。

「ファイル」メニューから、「その他」、「オプション」、「アドイン」の順に開きます。
画面下側の「管理」の横にある「設定」を開きます。
「アドイン」メニューの「ソルバーアドイン」、「分析ツール」にチェックを入れてOKを押します。
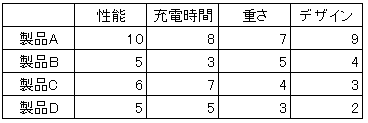
データの準備
今回は四種類のモバイルバッテリーに対して「性能、充電時間、重さ、デザイン」という項目の評価を準備しました。このデータで主成分分析をしていきましょう。
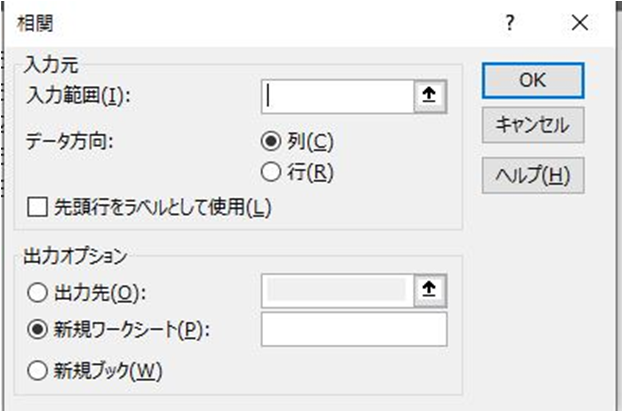
相関係数行列を求める
主成分分析を行うには「相関係数行列」から計算を行う方法と「分散共分散行列」から計算を行う方法がありますが、基準化などを考えなくてよく、エクセルで一発で算出できる相関係数行列を使用していきましょう。
「分析」、「データ分析」、「相関」の順に選択し、「入力範囲」に入力したデータ、「出力先」に適当なセルを選択します。
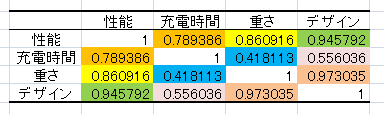
下記のようにデータが作成されます。図のように相関係数は半分しか表示されていないので、縦列をコピーして「形式を選択して貼り付け」を選択、「行列を入れ替える」にチェックを入れ、貼り付けていきます。
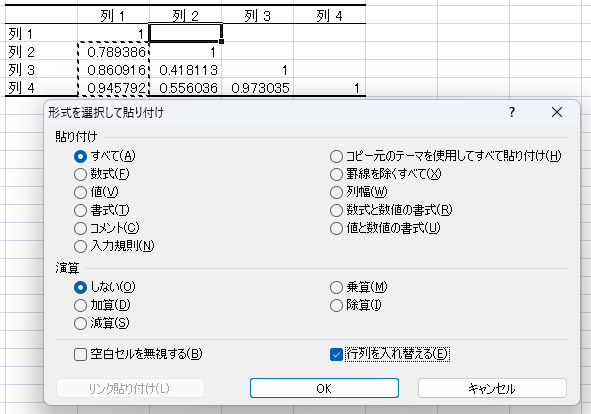
念のために確認ですが、図の同じ色の部分が同じ値になります。
仮の主成分を設定する
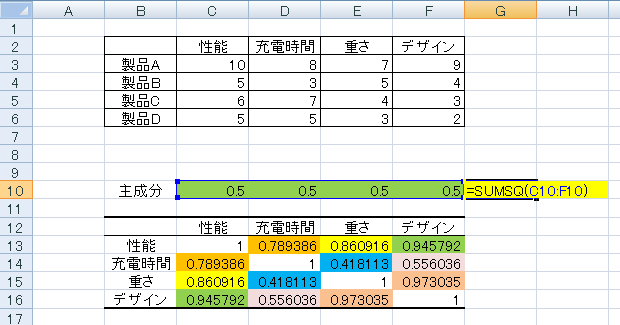
この後第一主成分、第二主成分、第三主成分、第四主成分の順に求めるので、各成分の上に仮の主成分を置きます。今回は0.5と置きました。後ほど計算するので仮の値で大丈夫です。
次に主成分の平方和を求めます。下図のように仮の主成分の平方和を表示する欄(=SUMSQ())を作成しておきます。後ほど主成分を検討する際に、主成分はその平方和を1とするため、この欄が1知なるように制約をかけながら平方和を計算していくためです。
制約条件部分はわかりやすいように黄色にしておきます。
主成分スコアを求める
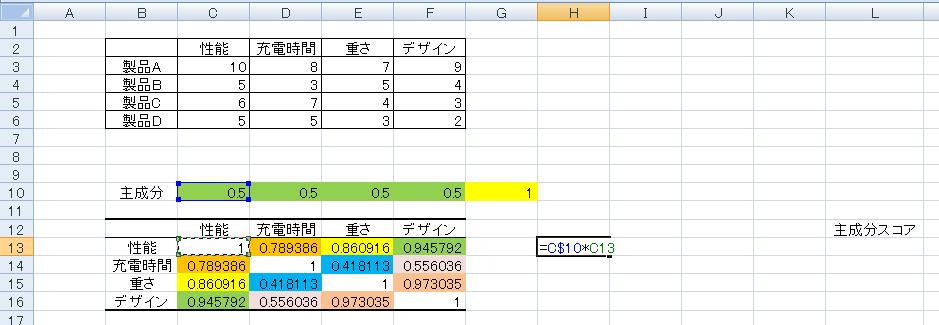
仮の主成分を用いて各データの主成分スコアを求めます。エクセルで計算しやすくするため、各項目の積を上記のように「仮の主成分」x「各データ」を計算します。この時に、コピーしやすくするよう、主成分の「行」は「$」でロックしておきます。
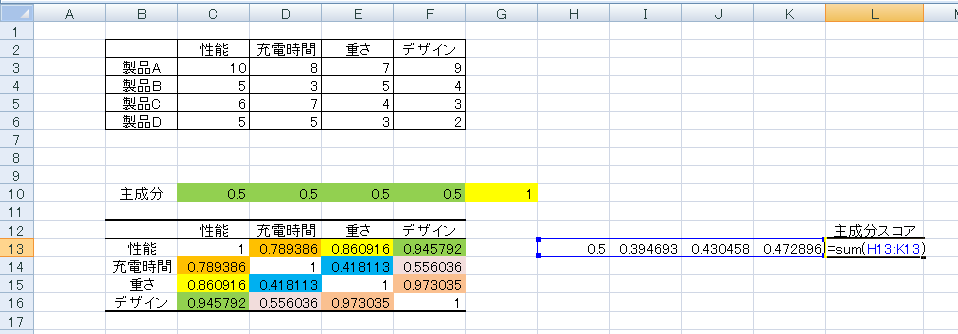
各列にも数式をコピーし、最後にその合計を「sum」でとってやることにより主成分スコアを算出します。その後、下の行にもコピーすれば完成です。
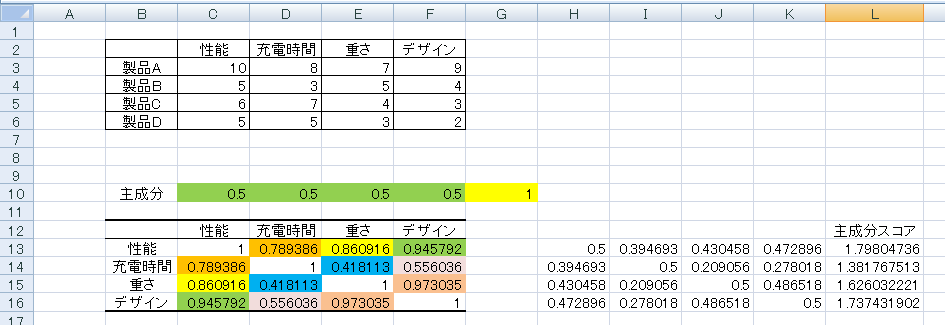
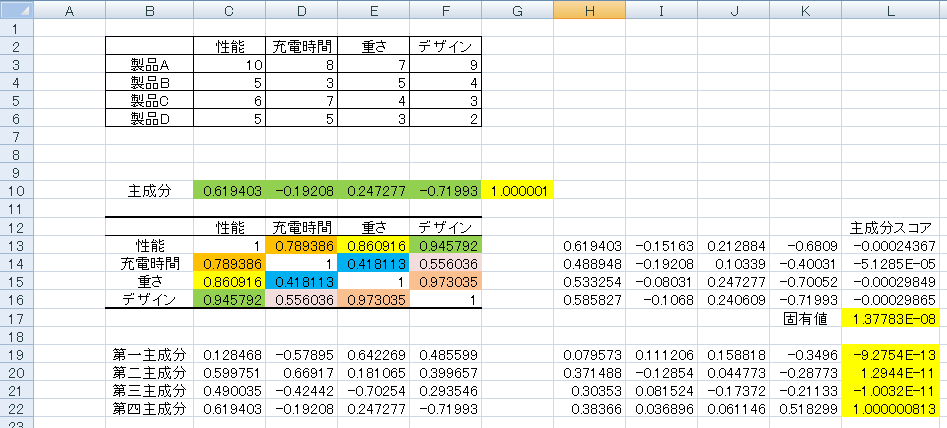
固有値の算出
先ほど求めた各主成分スコアの分散が固有値になるので、以下のように「var関数」で固有値を求めます。
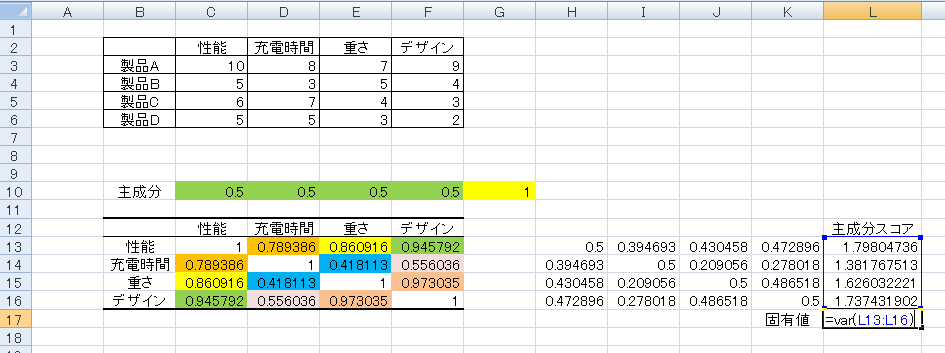
下図のような形になりました。
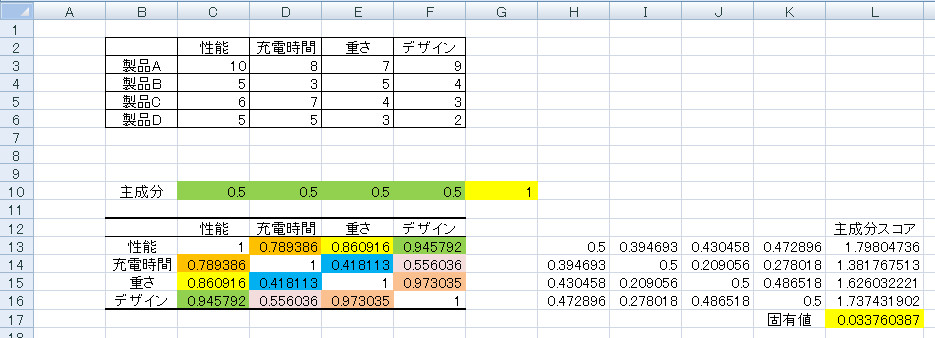
主成分分析で行いたいのは、元のデータをあるベクトルで変換した際に、その主成分スコアのばらつきである主成分スコアの分散である固有値を最大にするベクトルを探す作業です。
これはデータのばらつきがっとも大きい軸、つまり情報を最も持っている軸を探し出す行為で、上の図で言うと主成分の平方和「G10」が1で、かつ固有値「L17」が最大になる主成分「C10、D10、E10、F10」を探すことと同値になります。
第一主成分を算出する
では、そのもっとも固有値の大きくなる主成分を探していきましょう。
本来であればここで「ラグランジュ未定乗数」で偏微分した式を連立式にして解くことで正解を求めることができるのですが、今回の主旨はエクセルで「簡単に」解くことなので、「ソルバー」を利用して簡単に数値を求めましょう。
ソルバーは式を解いて値を求めるものではなく、値を繰り返し入れることによりあてはまる数値を求めるものです。したがって、解と完全に一致するものではありません。
上記のようにソルバーによる解法はPythonの解と必ずしも一致するものではありませんが、求めているものはPythonで求めているものと意味的には同じものになります。
ただ、手間を考えてもPythonで解いた方が簡単なので、以下の記事を参考にPythonでの解法にもぜひ挑戦してみてください。その際、わからないことはTech Teacherにぜひお問い合わせください!

ソルバーを使用していきます。「データ」、「分析」、「ソルバー」の順に開いてください。下のようなダイアログが表示されます。
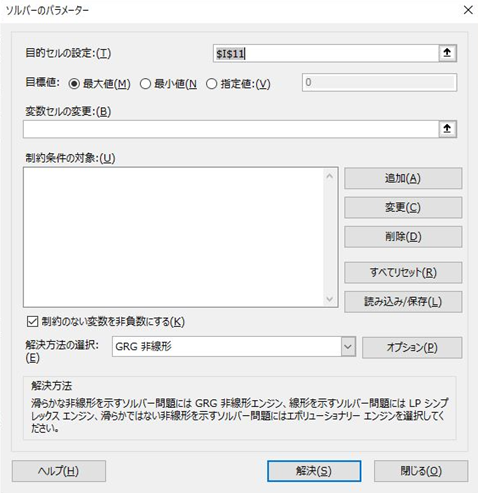
先ほど記したように「L17」を最大にする「C10、D10、E10、F10」の値を、「G10」が1である条件の下で探します。
「目的セルの設定」に「L17」を、これを最大にしたいので「目標値」に「最大値」を、「変数セルの変更」に「C10:F10」をそれぞれ入力してください。
その後、制約条件の対象で「追加」、「G10=1」と入力していきます。これで「解決」を押すと先ほど設定した「C10:F10」の値が更新されます。
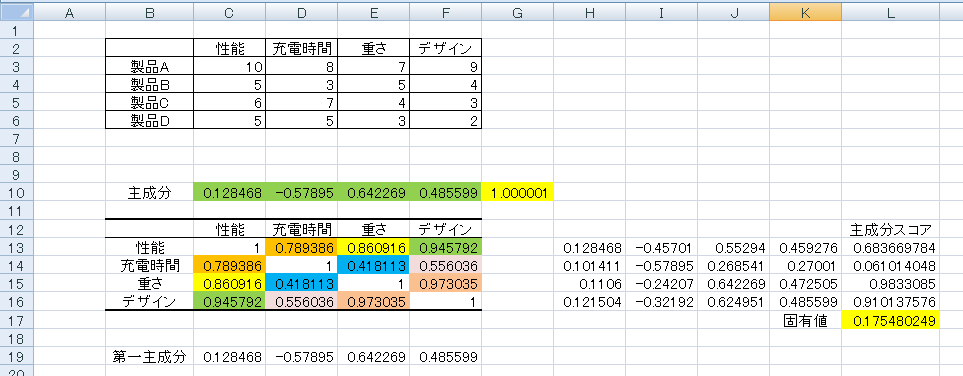
この条件に合う数値が「C10」から「F10」に入力されるので、これを数値で「C19」に貼り付けます。これが「第一主成分」になります。
第二主成分を算出する
第二主成分は第一主成分と直行し、その中で固有値が最大になる軸になります。先ほどソルバーで出した主成分の条件に「第一主成分に直交する」という条件を追加します。
「H19」から「K19」に、「H13」から「K13」のセルをコピーして貼り付けます。この状態で「L19」に先ほどの「H19」から「K19」の合計、「sum(H19:K19)」を入力します。これで「L19」が第一主成分とこれから求める主成分、緑色のセルとの内積になります。これが「0」になると、求めたい「第一主成分に直交する」という条件が成立します。
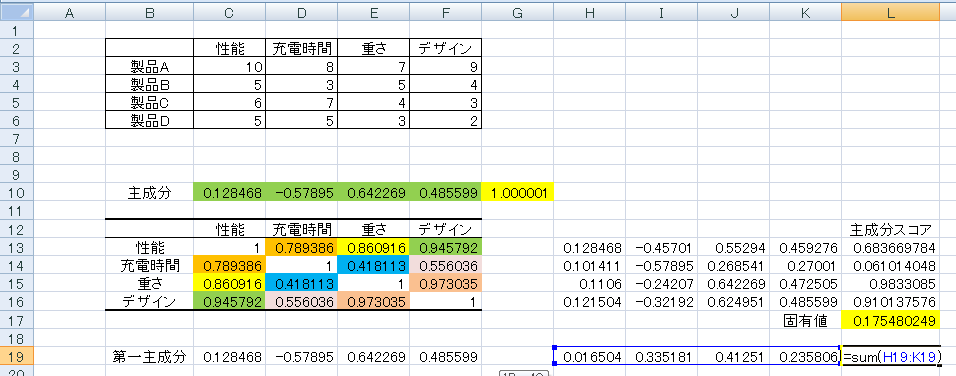
したがって、先ほどの「L19」を黄色にし、先ほどのソルバーの条件に「L19=0」を追加して再度主成分を求めます。
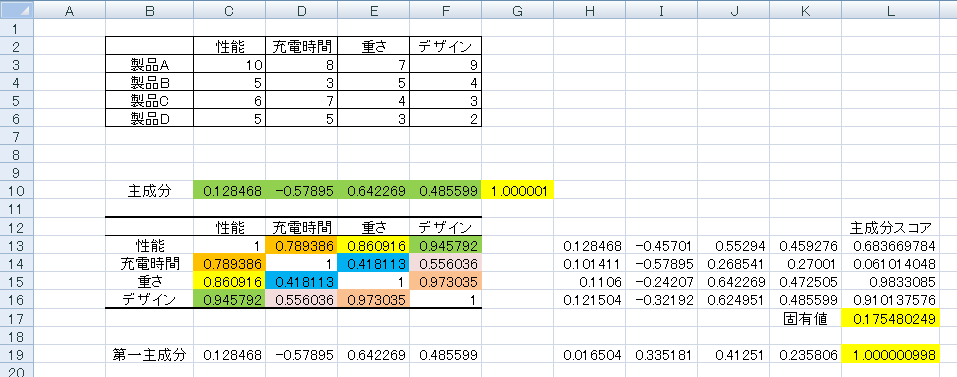
この状態で解決された答えが第二主成分となります。
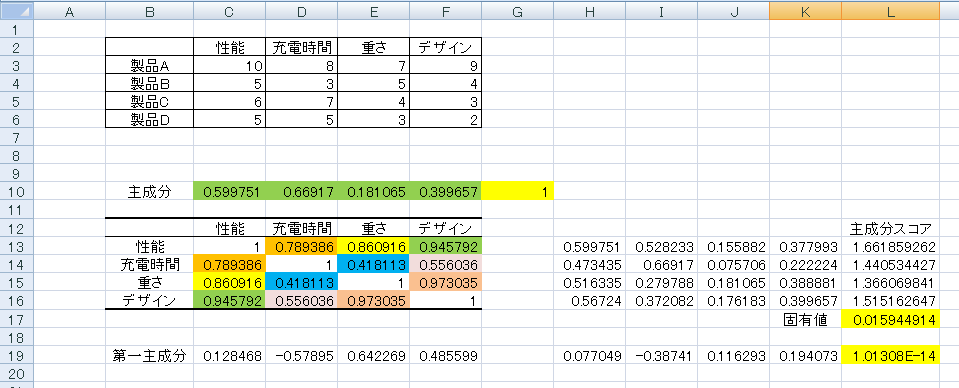
第三主成分、第四主成分を算出する
第三主成分、第四主成分も同様です。第三主成分は第一主成分、第二主成分に直交するので同様に第二主成分を下方に書き出して「L20=0」という条件を追加、同様に第四主成分は第一主成分から第三主成分まですべてに直交する条件を追加して算出します。
結果の見方
元データの変換
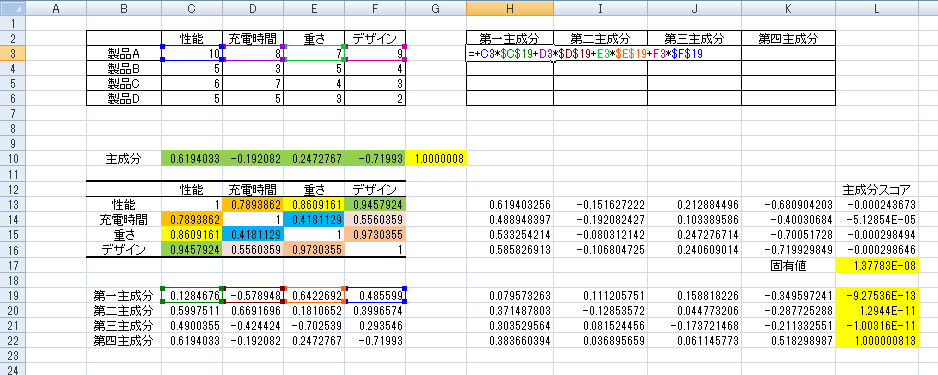
ではここからは先ほど出した軸をもとに、元データを変換してみましょう。「H3」から「K6」に変換後の数値を記入する欄を設けました。
まずは製品Aと第一主成分のベクトルで内積をとると製品Aの第一主成分が出るので「H3」に「C3*$C$19+D3*$D$19+E3*$E$19+F3*$F$19」と入れます。「$」は後々式をコピーすることを考えて入れています。
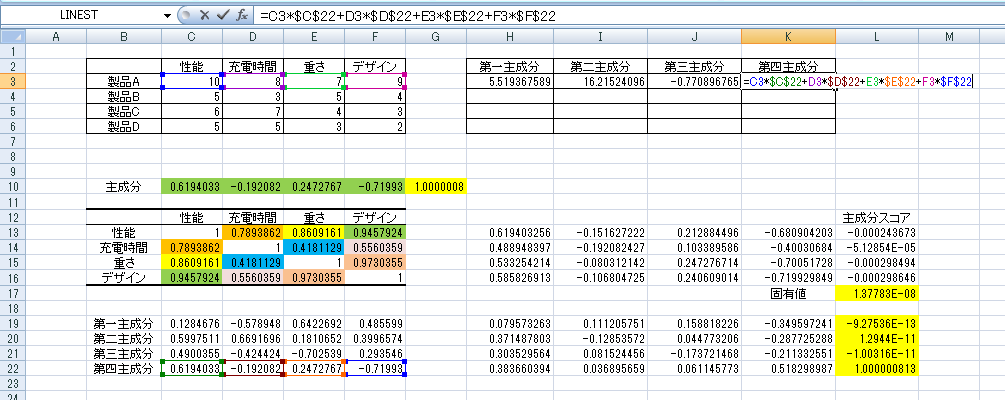
同様に第二主成分、第三主成分、第四主成分も変換する式を入力していきます。
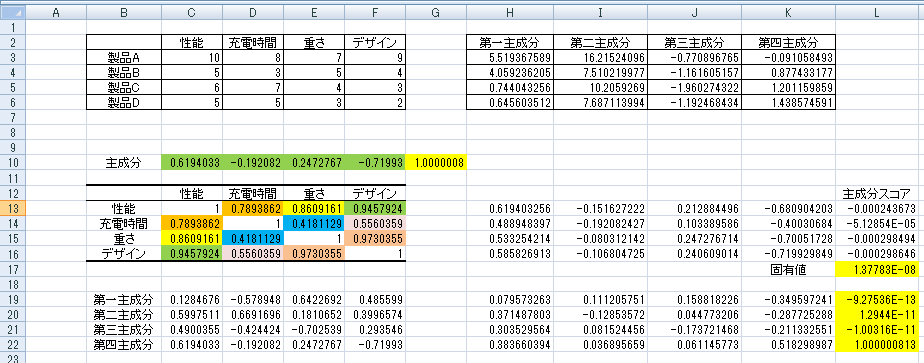
その後、「製品D」の部分まで式をコピーして元データのデータ変換完了です。
グラフでの表示とその意味
では、変換したデータを使用してグラフを描いてみましょう。
元のデータでは「性能」「充電時間」「重さ」「デザイン」という4つの情報を持っていましたので、一度にグラフにするには4次元のグラフを描く必要があり、事実上グラフに表すことができませんでした。
今回このデータを変換して第一主成分、第二主成分だけでたくさんの情報を持たせたので、この2軸だけで散布図を描いてみましょう。これは2次元のグラフなのでエクセルで簡単に描くことが可能です。
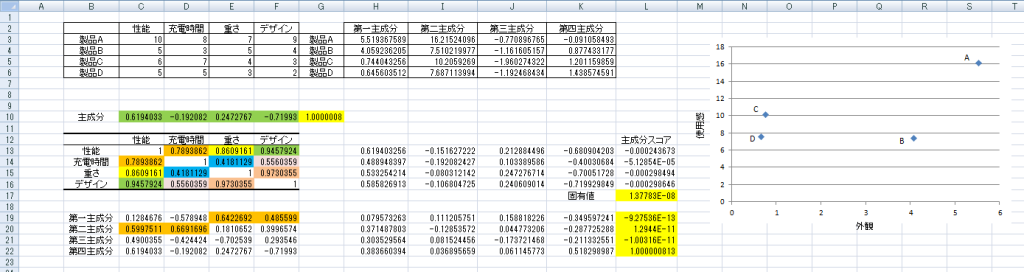
上記のように右側に散布図を書くことができましたが、これが何を意味しているのか見ていきましょう。各主成分がどのような情報を持っているかは左下の各主成分の内訳をみることで理解可能です。
第一主成分は橙色にした部分「重さ」や「デザイン」の情報を多く持っており、第二主成分は「性能」や「充電時間」の情報を多く持っています。したがって、第一主成分を「外観」第二主成分を「使用感」と名付けてみました。
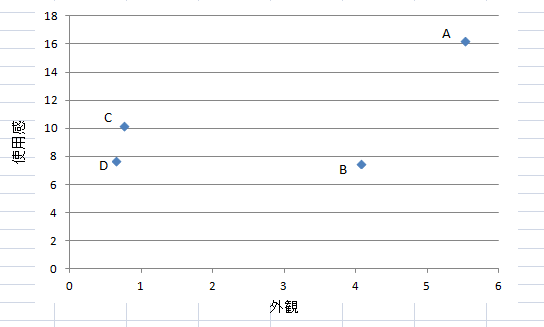
こう見ると、「A」は使用感も外観もよく、「C」や「D」は外観があまりよくないようです。では、これをもとのデータで確認してみると「A」はすべての得点がまんべんなくよく、「C」や「D」は重さやデザインの数値が低いことがわかります。
今回は説明のために少数の変数で行っていますが、主成分分析はこのようにたくさんの情報を少ない軸にまとめ、傾向をつかむ際に効果を発揮します。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
まとめ
今回はエクセルで主成分分析をする方法を見てきました。文中にあるように、Pythonで主成分分析をした方が簡単かつ正確に実施可能です。とはいえPythonはどうしてもとっつきにくいという方はこの際Tech Teacherに相談してみてはいかがでしょうか。Pythonを使用すれば今回のような処理を非常に簡単に解決できるようになります。









