連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第10章では、「母平均の区間推定(母分散が既知の場合)」について解説します。
初学者も理解しやすいように丁寧に解説しているので、ぜひ最後までご覧ください。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章：平均・分散などの基本統計量
2章：相関関係
3章：確率の基本
4章：条件付き確率・ベイズの定理
5章：期待値
6章：代表的な確率分布
7章：母集団と標本
8章：標本平均・不偏分散
9章：中心極限定理
10章：母平均の推定(分散既知)
11章：母平均の推定(分散未知)
12章：仮説検定
13章：正規分布を用いた検定
14章：【t検定】母平均を検定
15章：【F検定】分散に差があるか？
16章：ウェルチの検定
17章：カイ2乗検定
18章：分散分析
19章：回帰分析
本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。
区間推定
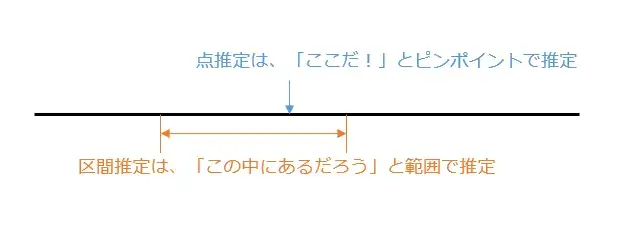
復習：区間推定とは
区間推定は、母数を1つの値ではなく、入る区間（幅）で推定します。
点推定では母数を単一の値で推定します。
一方、区間推定では母数が特定の確率（たとえば90％や95％）で存在すると推定される区間を求めることを目的としています。
引用：https://avilen.co.jp/personal/knowledge-article/statistical-estimation/
「標本」や「区間推定」など統計の基本用語は下記の記事でまとめているので、統計学初学者の方はぜひご覧ください。
信頼区間の正しい解釈
引用：https://bellcurve.jp/statistics/course/8891.html
信頼区間を誤って理解している方も多いので、ここで詳しく解説していきます。
例として、母平均の区間推定について考えます。
信頼区間を理解する上で大切なことは、
- 母平均は分からないが決まった値である
- 標本は確率的に決まる値である
ということです。
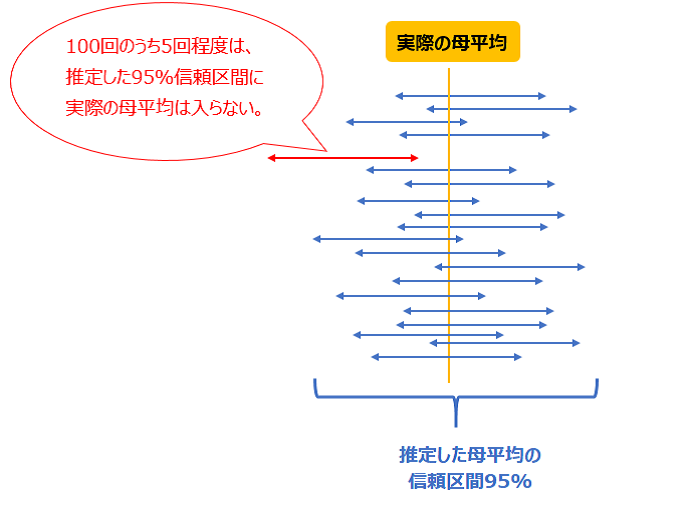
したがって、図のように区間推定を複数回行うと、母平均の値は一定ですが、信頼区間は区間推定を行うたびに変わります。
95%信頼区間とは、標本によって確率的に算出される区間のうち95%の区間が母平均を含むということを意味します。
もちろん、この「95%」は状況によって「90%」「98%」などに変わります。
ありがちな間違えとして、
95%の確率で、母平均uは
$$ a \leq u \leq b $$
という解釈です。
これは母平均を定数でなく、確率的に変換する値として捉えているため誤っています。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
母平均の区間推定(母分散が既知)
では実際に、母平均の区間推定を行います。
問題
ある高校生の身長を調査するために、10人のサンプルを取りました。
以下はそれぞれの学生の身長です。（単位：cm）
163, 168, 170, 165, 172, 167, 162, 169, 171, 166
また、母分散は「\(\sigma^2 = \scriptsize 4^{2}\)」と既知であるとします。
さらに、母集団の分布は「正規分布」であると仮定します。
この時、高校生の身長の母平均uを95%信頼区間で推定してください。
まず、標本平均\(\bar{X}\)を求めます。
$$
\begin{align*}
\bar{X} &= \frac{\scriptsize 163 + 168 \dots + 171 + 166}{\scriptsize 10}\\
&= \scriptsize 167
\end{align*}
$$
母集団が「平均u」「分散\(\sigma^{\scriptsize 2}\)」の正規分布の時、標本平均は「平均u」「分散\(\frac{\sigma^{\scriptsize 2}}{n}\)」の正規分布に従います。
nを十分大きいとみなすと、中心極限定理から同様のことが言えます。
中心極限定理では、nが大きい場合「近似的に標本平均が正規分布に従う」とみなせました。
しかし、母集団が正規分布と仮定した場合、nの個数によらず「ポイント」のような事実が成り立つことが知られています。
中心極限定理について詳しく知りたい方は下記の記事をご覧ください。
したがって、この問題では標本平均が「平均：u」「分散：\(\frac{\scriptsize 4^{2}}{\scriptsize10}\)」の正規分布に従います。
そして、正規分布では正規分布表や計算サイトを用いると下記のような「確率と区間の対応」を得ることができます。
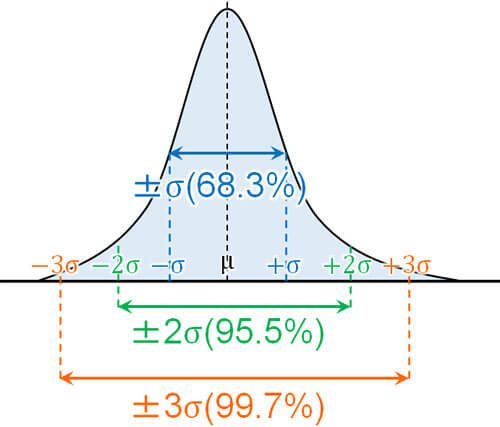
引用：https://hatsudy.com/jp/interval-estimation.html
図より、「平均：u」「分散：\(\sigma^2\)」の正規分布の場合、中心から「\(\pm\sigma\)」離れた区間内は「68.3%」に対応します。
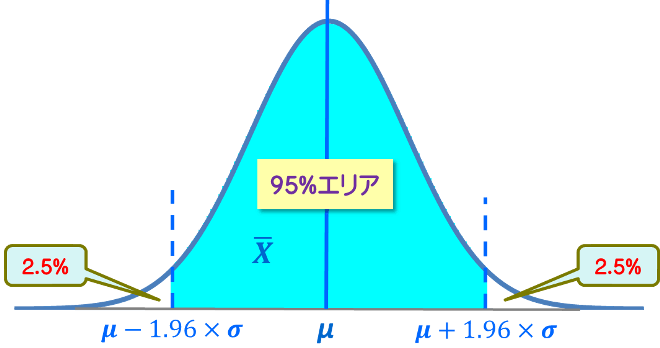
正規分布では、標本平均\(bar{X}\)が「u-1.96\sigma以上」「u+1.96\sigma」以下に入っている確率が95%です。
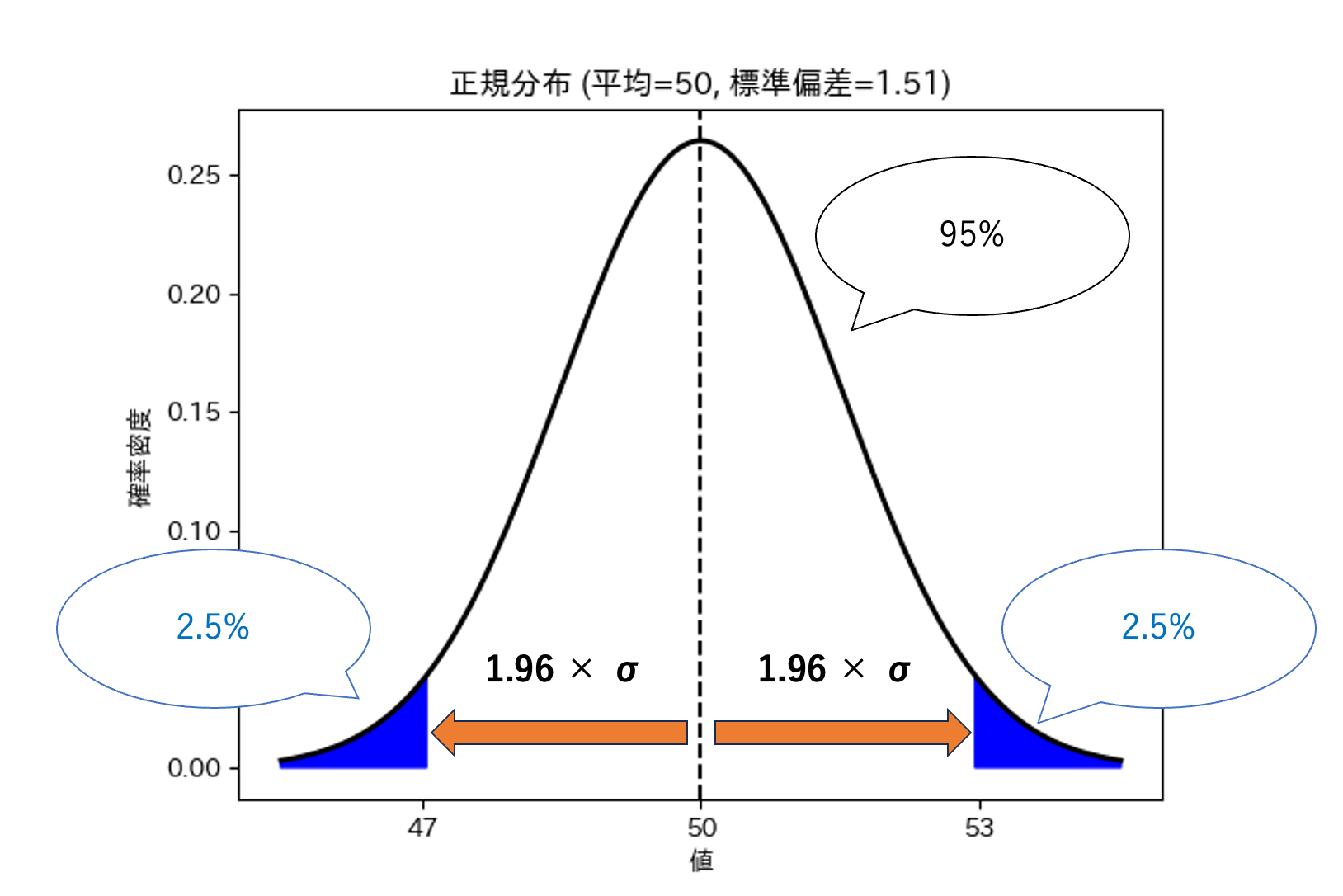
正規分布は確率密度関数なので、全体の面積は「1」となります。
すなわち、95%エリアの面積は「0.95」です。
標本平均\(\bar{X}\)が「平均：u」「分散：\(\frac{\scriptsize 4^{2}}{\scriptsize10}\)」の正規分布について考えているので、
95%信頼区間では
$$
u – {\scriptsize1.96} \times \frac{\scriptsize 4}{\scriptsize \sqrt{10}} \leq \bar{X} \leq u + {\scriptsize1.96} \times \frac{\scriptsize 4}{\scriptsize \sqrt{10}}
$$
となります。
式変形をすると
$$
\bar{X} – {\scriptsize1.96} \times \frac{\scriptsize 4}{\scriptsize \sqrt{10}} \leq u \leq \bar{X} + {\scriptsize1.96} \times \frac{\scriptsize 4}{\scriptsize \sqrt{10}}
$$
標本平均\(\bar{X}\ = \scriptsize 167\)なので
$$
\scriptsize 167 – {\scriptsize1.96} \times \frac{\scriptsize 4}{\scriptsize \sqrt{10}} \leq u \leq \scriptsize 167 + {\scriptsize1.96} \times \frac{\scriptsize 4}{\scriptsize \sqrt{10}}
$$
以上より、高校生全体の身長の母平均uの95%信頼区間は
$$
164.5 \leq u \leq 169.5
$$
と求めることができました。
まとめ：母平均の区間推定(母分散が既知)
母平均u、母分散\(\sigma^{\scriptsize 2}\)の正規母集団に対する信頼度mの信頼区間は
$$
\bar{X} – k\times \frac{\sigma}{\sqrt{n}} \leq u \leq \bar{X} + k\times \frac{\sigma}{\sqrt{n}}
$$
で得られる。
kは「分散1、平均０の標準正規分布」の両側100(1-m)%点である。
(95%の場合：1.96)
練習問題を解いて、区間推定に慣れていきましょう。
練習問題
母分散が「\(\sigma^2 = \scriptsize 5^2\)」である正規母集団から10個の無作為標本を抽出して標本平均\(\bar{X}\) = 12.8 を得ました。母平均の95%信頼区間を求めてください。
(母集団分布が正規分布である母集団を正規母集団と言います。)
引用：区間推定
先ほどの問題と同様に考えると、母集団分布が正規分布に従うので、標本平均\(\bar{X}\)は、「平均：u」、「分散：\(\frac{\scriptsize 5^2}{\scriptsize 10}\)」の正規分布に従います。
したがって、95%信頼区間で標本平均が満たす式は
$$
u – {\scriptsize1.96} \times \frac{\scriptsize 5}{\scriptsize \sqrt{10}} \leq \bar{X} \leq u + {\scriptsize1.96} \times \frac{\scriptsize 5}{\scriptsize \sqrt{10}}
$$
式変形すると、
$$
\bar{X} – {\scriptsize1.96} \times \frac{\scriptsize 5}{\scriptsize \sqrt{10}} \leq u \leq \bar{X} + {\scriptsize1.96} \times \frac{\scriptsize 5}{\scriptsize \sqrt{10}}
$$
標本平均\(\bar{X}\) = 12.8なので、
$$
\scriptsize 12.8 – {\scriptsize1.96} \times \frac{\scriptsize 5}{\scriptsize \sqrt{10}} \leq u \leq \scriptsize 12.8 + {\scriptsize1.96} \times \frac{\scriptsize 5}{\scriptsize \sqrt{10}}
$$
以上より、母平均uの95%信頼区間は
$$
\scriptsize 9.70 \leq u \leq \scriptsize 15.6
$$
と求めることができました。
