連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第15章では、「F検定」について解説します。
「F検定はいつ使うのか」や「F検定の手順」など、F検定を基本から丁寧に解説しています。
初学者も理解しやすいように丁寧に解説しているので、ぜひ最後までご覧ください。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章：平均・分散などの基本統計量
2章：相関関係
3章：確率の基本
4章：条件付き確率・ベイズの定理
5章：期待値
6章：代表的な確率分布
7章：母集団と標本
8章：標本平均・不偏分散
9章：中心極限定理
10章：母平均の推定(分散既知)
11章：母平均の推定(分散未知)
12章：仮説検定
13章：正規分布を用いた検定
14章：【t検定】母平均を検定
15章：【F検定】分散に差があるか？
16章：ウェルチの検定
17章：カイ2乗検定
18章：分散分析
19章：回帰分析
本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。
F検定とは
F検定は、2つの正規母集団の母分散（ばらつき）が等しいかを検定するときに利用します。
したがって、正規母集団Aの母分散を\({\sigma_A}^{2}\)、正規母集団Bの母分散を\({\sigma_B}^{2}\)とすると、
- 帰無仮説：\({\sigma_A}^{2} = {\sigma_B}^{2} \)
- 対立仮説：\({\sigma_A}^{2} \neq {\sigma_B}^{2} \)
と設定します。
帰無仮説、対立仮説など仮説検定の内容に不安がある方は、こちらの記事から復習をしましょう。
2つの母分散「\({\sigma_A}^{2}\)と\({\sigma_B}^{2}\)が等しいか」を検証する際に、母分散を直接計算することは基本的に不可能です。
そのため、標本データから計算でき、母分散と似た性質を持つ不偏分散を利用して検定します。
不偏分散\({U^2}\)は以下の式で求められます。
$$ U^2 = \frac{\scriptsize 1}{n – \scriptsize1} \sum_{i=1}^n (X_i – \bar{X})^2 $$
不偏分散は以下の記事で詳しく解説しています。
ここで、検定統計量Fを
$$
\begin{align*}
F &= \frac{{U_A}^{2}/{\sigma_A}^{2}}{{U_B}^{2}/{\sigma_B}^{2}}\\
&= \frac{{\sigma_B}^{2}}{{\sigma_A}^{2}} \cdot \frac{{U_A}^{2}}{{U_B}^{2}}
\end{align*}
$$
と設定します。
この検定統計量Fは、帰無仮説が真（\({\sigma_A}^{2} = {\sigma_B}^{2} \)）の場合
$$
F = \frac{{U_A}^2}{{U_B}^2}
$$
となります。
母集団Aの標本数を「m」、母集団Bの標本数を「n」とすると
検定統計量Fが、自由度(m – 1, n – 1)のF分布に従うことを利用して、仮説検定を行います。
F分布については、次の見出しで解説します。
F検定のまとめ：
2つの正規母集団の母分散が等しいかを、 統計検定量\(F = \frac{{U_A}^2}{{U_B}^2}\)を用いて検定する。
- 帰無仮説：\({\sigma_A}^{2} = {\sigma_B}^{2} \)
- 対立仮説：\({\sigma_A}^{2} \neq {\sigma_B}^{2} \)
検定統計量Fが、自由度(m – 1, n – 1)のF分布に従う
F検定には、「標準偏差が等しい正規分布に従う複数の群の平均が等しい」を検定する別のものもあることに注意しましょう。
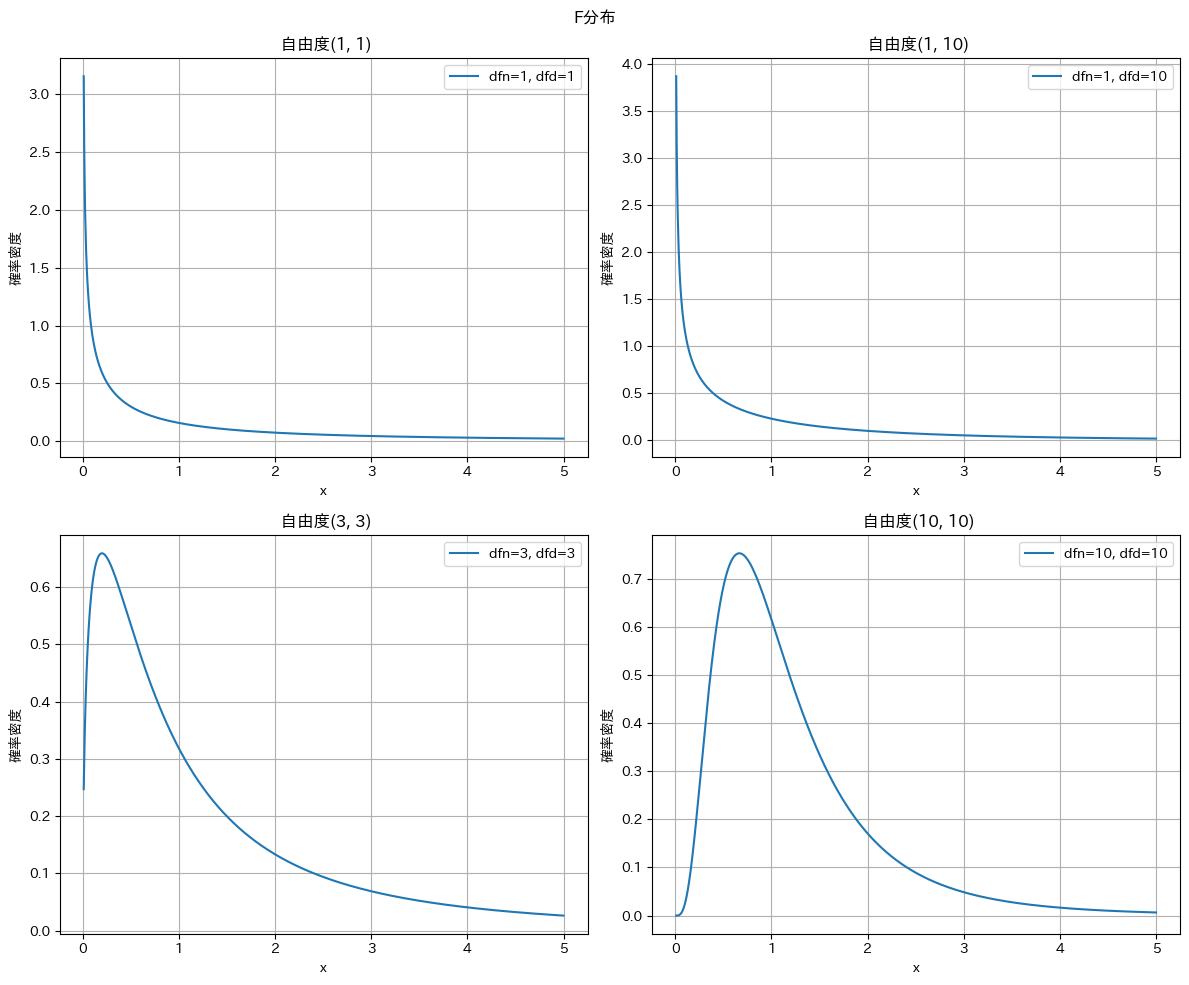
F分布
F分布の特徴について解説していきます。
先ほど学習したように、F分布は2つの母集団の分散が等しいか検定する場合に利用します。
そして、F分布の特徴は
- グラフの概形は左右非対称
- 右に裾が長い
- 2つの自由度から定まる
という特徴を持っています。
F分布のグラフの概形を自由度(1,1)、(1,10)、(3,3)、(10,10)で見てみましょう。
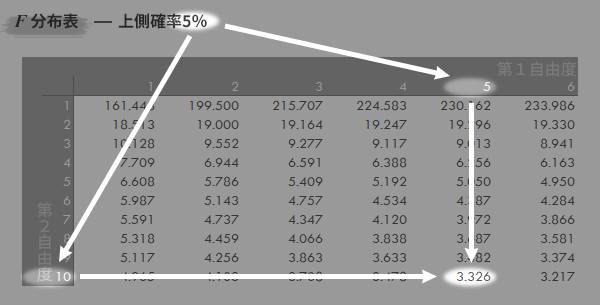
また、上側5%点のF分布表は以下のとおりです。
例として、自由度(5,10)のF分布の上側5%点を読み取っています。
引用：https://bdastyle.net/tools/probability-and-percentile/f-distribution.html
2つの母集団A,Bは自由に設定・入れ替え可能ですが、F分布を利用するときは、
$$ \frac{U_1}{U_2} > 1 $$
となるように\(U_1\)、\(U_2\)を入れ替えましょう。
下側パーセント点の表は与えられていない場合も多いです。
そのため、下側パーセント点はF分布表(上側)において 自由度を入れ替えたFの逆数で求めます。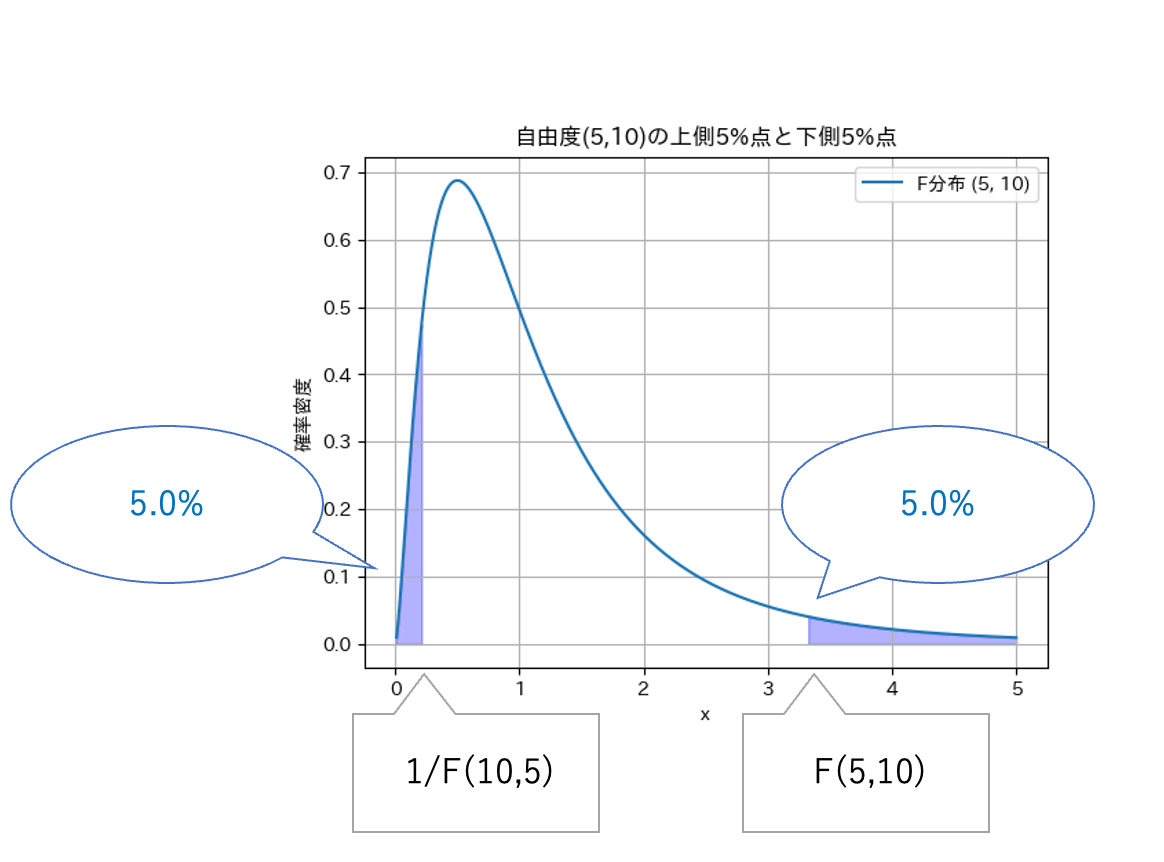 
なお、自由度(m,n)の上側5%点をF(m,n)と表記しています。
必要に応じて、適切なパーセント点の表を用いましょう。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
F検定の練習問題
練習問題
ある薬の効果を検証するために、病院Aと病院Bでそれぞれ治験が行われました。
病院Aでは100人の患者が、病院Bでは120人の患者が治験に参加しました。
病院Aの治験参加者の血圧値の不偏分散は\(20^2\)であり、病院Bの治験参加者の血圧値の不偏分散は\(25^2\)です。
有意水準を0.05として、「病院Aと病院Bの患者の血圧値の分散が等しいかどうか」をF検定を用いて検定してください。
標本データから読み取ると、病院Bの方が分散が大きいと考えられます。
しかし、偶然、病院Bの治験参加者の血圧値の分散が大きくなった可能性もあります。
F検定を用いて、病院Aと病院Bの患者の血圧値の分散が等しいか検定していきましょう。
F検定も仮説検定の1種なので、「仮説検定の手順」にしたがって、検定していきましょう。
仮説検定の手順
- 帰無仮説\(H_0\)、対立仮説\(H_1\)を設定する
- 帰無仮説\(H_0\)を真として、統計量の分布を求める
- 有意水準を決める
- 有意水準と統計量の分布から、棄却域を設定する
- 標本から得られた結果が確率的に起こり得るなら、帰無仮説\(H_0\)を受容・対立仮説\(H_1\)を棄却
- 標本から得られた結果が確率的に起こり得ないなら、帰無仮説\(H_0\)を棄却・対立仮説\(H_1\)を採択
仮説検定について詳しく知りたい方は下記の記事よりご覧ください。
①：帰無仮説\(H_0\)、対立仮説\(H_1\)を設定する
病院Aの患者の血圧値の母分散を\({\sigma_A}^2\)、病院Bの患者の血圧値の母分散を\({\sigma_B}^2\)とします。
また、病院Aの患者の血圧値の不偏分散を\({u_A}^2\)、病院Bの患者の血圧値の不偏分散を\({u_B}^2\)とします。
「病院Aと病院Bの患者の血圧値の分散が等しいか」を検定するので
- 帰無仮説：\({\sigma_A}^{2} = {\sigma_B}^{2} \)
- 対立仮説：\({\sigma_A}^{2} \neq {\sigma_B}^{2} \)
と設定します。
②：帰無仮説\(H_0\)を真として、統計量の分布を求める
帰無仮説を真とするため、
$$ {\sigma_A}^{2} = {\sigma_B}^{2} $$
の元で進めていきます。
先ほど解説した通り、
\({\sigma_A}^{2} = {\sigma_B}^{2} \)の時、
$$
F = \frac{{U_B}^2}{{U_A}^2}
$$
となり、Fが自由度(119,99)のF分布に従います。
$$ \frac{u_B}{u_A} > 1 $$
より、対応する\(U_A\)、\(U_B\)は
$$
F = \frac{{U_B}^2}{{U_A}^2}
$$
と入れ替える。
③：有意水準を決める
今回は問題文で、有意水準αが
$$ \alpha = 0.05 $$
と定められています。
実際の業務や研究で行う場合は、データ数や状況に応じて適切に設定しましょう。
④：有意水準と統計量の分布から、棄却域を設定する
今回は両側5%検定を行うため、上側2.5%点と下側2.5%を求めます。
- 上側2.5%点：\(p_+\)
- 下側2.5%点：\(p_-\)
とします。
そして、F分布の自由度(k,l)の上側2.5%点を
$$ F_{0.025}(k,l) $$
と表します。
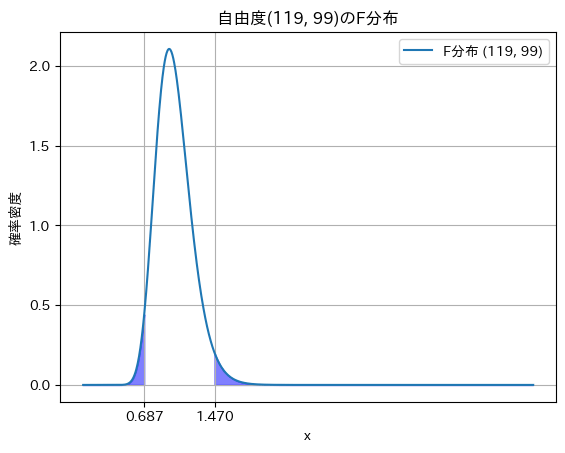
Fが自由度(119,99)のF分布に従うので、計算サイトやf分布表を用いると
$$ p_+ = F_{0.025}(119,99) \simeq 1.47 $$
$$ p_- = \frac{1}{F_{0.025}(99,199)} \simeq 0.687 $$
となります。
よって、棄却域は
$$ F \leq 0.687 \quad 1.47 \leq F $$
⑤：標本から得られた結果が確率的に起こり得るなら、帰無仮説\(H_0\)を受容・対立仮説\(H_1\)を棄却
⑥：標本から得られた結果が確率的に起こり得ないなら、帰無仮説\(H_0\)を棄却・対立仮説\(H_1\)を採択
標本データから得られるFの実現値fは
\begin{align*}
f &= \frac{{u_B}^2}{{u_A}^2} \\
&= \frac{25^2}{20^2} \\
&\simeq 1.56
\end{align*}
と求められます。
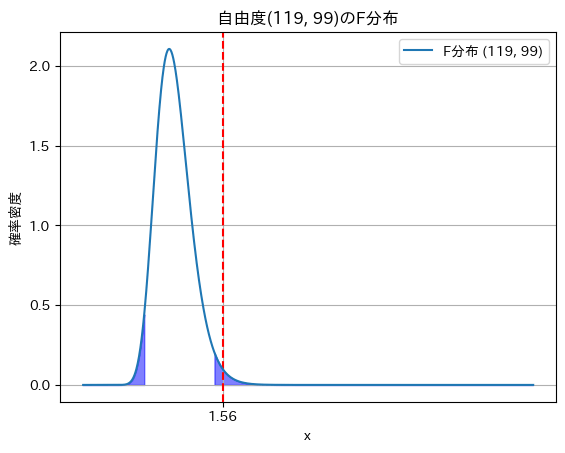
fが、棄却域
$$ F \leq 0.687 \quad 1.47 \leq F $$
内にあるため、「標本から得られた結果が確率的に起こり得ない」と解釈できます。
したがって、帰無仮説\(H_0\)を棄却・対立仮説\(H_1\)を採択します。
すなわち、「病院Aと病院Bの患者の血圧値の分散が等しくない」という結論が得られます。
