本連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第2章では、「相関係数」について説明します。
・相関係数とは何か?
・因果関係との違いは?
について解説します。
「相関の定義や性質」などの基本的な内容から、「擬似相関」などの発展的な内容も扱っています。
またコラムでは「指標に隠された罠」として、データを見るときの注意点を紹介したいと思います。
ぜひ最後までご覧ください。
以下の記事では、エクセルを使って「共分散」「相関係数」を求める方法を解説しています。

本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章:平均・分散などの基本統計量
2章:相関関係
3章:確率の基本
4章:条件付き確率・ベイズの定理
5章:期待値
6章:代表的な確率分布
7章:母集団と標本
8章:標本平均・不偏分散
9章:中心極限定理
10章:母平均の推定(分散既知)
11章:母平均の推定(分散未知)
12章:仮説検定
13章:正規分布を用いた検定
14章:【t検定】母平均を検定
15章:【F検定】分散に差があるか?
16章:ウェルチの検定
17章:カイ2乗検定
18章:分散分析
19章:回帰分析
相関関係とは?
相関関係
「相関関係がある」とは、2つの変数の間に直線関係に近い傾向が見られる状態のことを言います。
特に、一方の変数の増加に伴い、もう一方の変数も増加する場合「正の相関がある」と言います。
例として
- 気温とアイスクリームの売上
- 数学の点数と理科の点数
- 身長と体重
のような事象では正の相関が得られるでしょう。
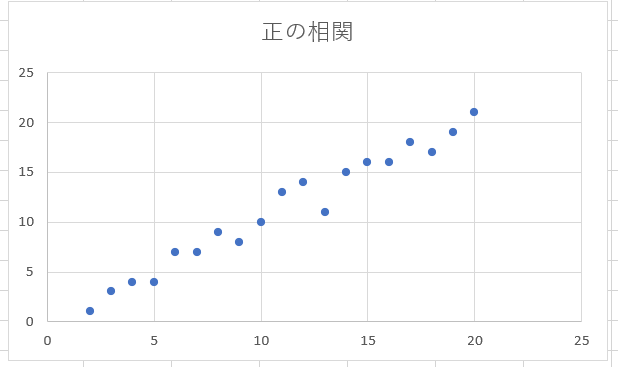
これに対し、一方の変数の増加に伴い、もう一方の変数が減少する場合、「負の相関がある」と言います。
例として
- 気温と暖房の使用量
- 先進国の失業率と実質経済成長率
- 遊ぶ時間とテストの点数
のような事象では負の相関が得られるでしょう。
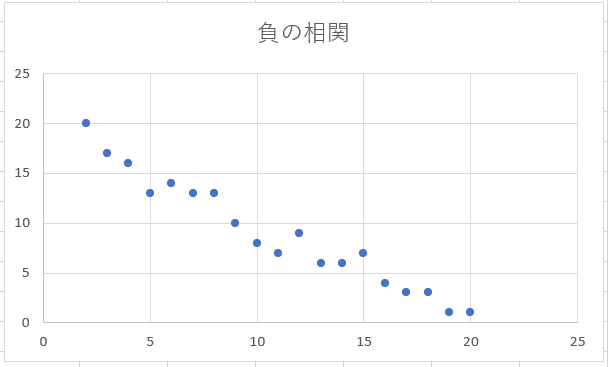
2つの変数間に直線的関係が見られない場合は「無相関である」と言います。
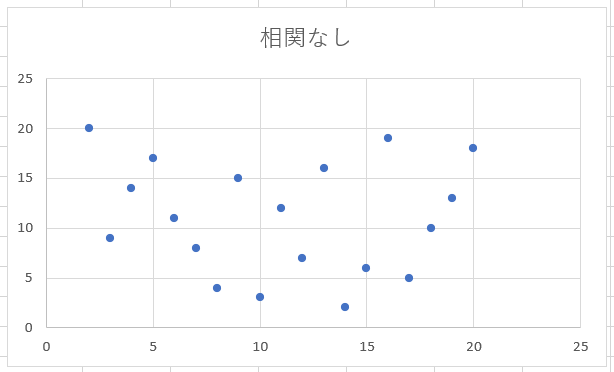
引用:https://www.northdetail.co.jp/blog/689/
相関関係の注意点 (発展)
様々な教材やインターネットの情報で、相関関係とは「2つの変数の間に関係がある」と定義されている場合が多いですが、より正確には「直線的な関係」を意味していることに注意しましょう。
下記画像のデータでは
- 二次関数
- 円
といった関係が読み取れそうですが、相関の強さを表す相関係数を計算すると0に近いです。
そのため「関係はあるが、相関関係は弱い」と言えるでしょう。
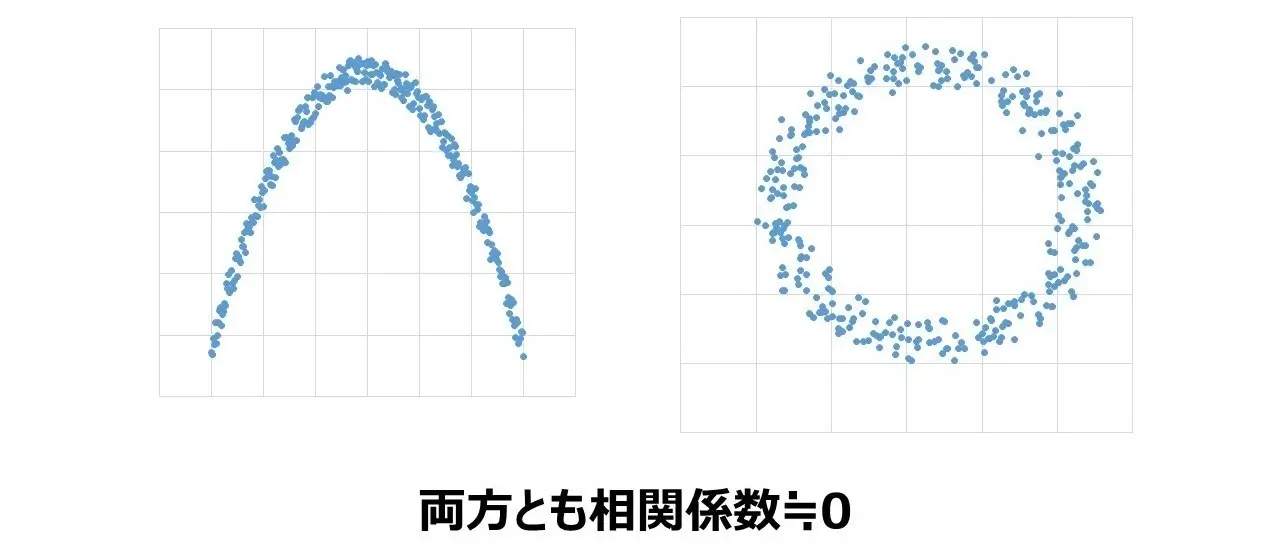
引用:https://www.bewith.net/gemba-driven/article/digital/entry-242.html
相関係数の定義
前述の内容ではグラフを見て、「相関がある」や「正の相関がある」などと判断しています。
しかし、グラフだけでは曖昧にしか相関の強さを判断できません。
そのため、次に数値から「相関関係があるか」を確認するための指標である相関係数を説明します。
共分散
まず相関係数を理解する上で重要な「共分散」について説明します。
共分散とは、二組の対応するデータ間の関係を表す数値を表す指標です。
共分散は下記のように定義されています。
$$ \text{cov(x,y)} = \frac{\scriptsize 1}{n} \sum_{i=1}^n (x_i – \bar{x})(y_i – \bar{y}) $$
Σに慣れていない人は下記の式で理解しましょう。
$$ \text{cov(x,y)} = \frac{(x_1 – \bar{x})(y_1 – \bar{y}) + (x_2 – \bar{x})(y_2 – \bar{y}) + \ldots + (x_n – \bar{x})(y_n – \bar{y}) }{n} $$
次に共分散の式の意味について解説します。
共分散は、「Xの偏差(個々の数値と平均値との差)」と「Yの偏差」の積の平均をとったものなので、「負×負→正」、「正×正→正」、「負×正→負」であることに注意すると
- 共分散が大きい(正)→ 正の相関がある
- 共分散が0に近い → 無相関である
- 共分散が小さい(負)→ 負の相関がある
となります。
下記の練習問題で共分散を求めてみましょう。
練習問題
あるクラスの生徒たちの数学と英語の月間テストの点数データがあります。
以下は、各生徒の数学と英語のテストの点数です。
| 数学の点数 (X) | 英語の点数 (Y) | |
| Aさん | 80 | 85 |
| Bさん | 75 | 70 |
| Cさん | 90 | 95 |
| Dさん | 85 | 80 |
| Eさん | 95 | 90 |
これらのデータを用いて、数学と英語のテストの点数の共分散を計算してください。
まず、Xの平均を求めます。
$$ \bar{x} = \frac{\scriptsize 80 + \scriptsize 75 + \scriptsize 90 + \scriptsize \scriptsize 85 + \scriptsize 95}{\scriptsize 5} = \scriptsize 85 $$
次にYの平均を求めます。
$$ \bar{y} = \frac{\scriptsize 85 + \scriptsize 70 + \scriptsize 95 + \scriptsize \scriptsize 80 + \scriptsize 90}{\scriptsize 5} = \scriptsize 84$$
以下の共分散の定義式を用いて計算する。
$$ \text{cov(x,y)} = \frac{\scriptsize 1}{n} \sum_{i=1}^n (x_i – \bar{x})(y_i – \bar{y}) $$
$$ \text{cov(x,y)} = \frac{(x_1 – \bar{x})(y_1 – \bar{y}) + (x_2 – \bar{x})(y_2 – \bar{y}) + \ldots + (x_n – \bar{x})(y_n – \bar{y}) }{n} $$
\[
\begin{align*}
\text{cov(x,y)} &= \frac{\{\scriptsize 80 – \scriptsize 85)(\scriptsize 85 – \scriptsize 84) + (\scriptsize 75 – \scriptsize 85)(\scriptsize 70 – \scriptsize 84) + \ldots + (\scriptsize 95 – \scriptsize 85)(\scriptsize 90 – \scriptsize 84)\}}{\scriptsize 5}\\
&= \frac{\{\scriptsize -5)(\scriptsize 1) + (\scriptsize -10)(\scriptsize -14) + \ldots + (\scriptsize 10)(\scriptsize 6)\}}{\scriptsize 5}\\
& = \frac{\scriptsize -5 + \scriptsize 140 + \scriptsize 55 + \scriptsize 0 + \scriptsize 60}{\scriptsize 5}\\
&= \scriptsize 50
\end{align*}
\]
共分散の値が「50」より、共分散が大きい(正)→ 正の相関があるということが読み取れます。
相関関係の定義式
先ほど説明した共分散により、二組の対応するデータ間の関係を数値化することができました。
しかし共分散では、データによってスケールが異なるので、「複数のデータ間で、どの相関が強いか・弱いか」比較することができません。
例えば、「100点満点のテスト」と「1000点満点のテスト」の共分散では、「1000点満点のテスト」から算出された共分散の絶対値が大きくなりやすいはずです。
この欠点を補うために相関係数を導入します。
相関係数とは、相関関係の強弱を-1以上・1以下までの数値で表したものです。
相関係数は「1に近いほど強い正の相関」を表し、「-1に近いほど強い負の相関」を表します。
この相関係数により、複数のデータ間で相関関係の強さを比較できるようになります。
相関係数rは下記のように定義されています。
$$ r = \frac{cov(X,Y)}{s_X \cdot s_Y} $$
$$
cov(X,Y):\text{共分散}\\
s_X:Xの 標準偏差\\
s_Y:Yの標準偏差\\
$$
「標準偏差」を忘れてしまった方は以下の記事で確認しましょう。

下記の練習問題で相関係数を求めてみましょう。
練習問題
あるクラスの生徒たちの数学と英語の月間テストの点数データがあります。
以下は、各生徒の数学と英語のテストの点数です。
| 数学の点数 (X) | 英語の点数 (Y) | |
| Aさん | 80 | 85 |
| Bさん | 75 | 70 |
| Cさん | 90 | 95 |
| Dさん | 85 | 80 |
| Eさん | 95 | 90 |
これらのデータを用いて、数学と英語のテストの点数の相関係数を計算してください。
前述の練習問題より
$$ cov(X,Y) = \scriptsize 50 $$
と求められました。
分散の定義式
$$ s^2 = \frac{\scriptsize 1}{n} \sum_{i=1}^n (x_i – \bar{x})^2 $$
より
\begin{align*}
{s_X}^2 &= \frac{(\scriptsize 80 – \scriptsize 85)^2 + (\scriptsize 75 – \scriptsize 85)^2 + \ldots + (\scriptsize 95 – \scriptsize 85)^2}{\scriptsize 5} \\
&= \scriptsize 50
\end{align*}
\begin{align*}
{s_Y}^2 &= \frac{(\scriptsize 85 – \scriptsize 84)^2 + (\scriptsize 70 – \scriptsize 84)^2 + \ldots + (\scriptsize 90 – \scriptsize 84)^2}{\scriptsize 5} \\
&= \scriptsize 74
\end{align*}
よって相関係数rは
\begin{align*}
r &= \frac{\scriptsize 50}{\sqrt{\scriptsize 50} \times \sqrt{\scriptsize 74}}\\
& \simeq \scriptsize 0.822
\end{align*}
相関係数の目安
相関係数は-1以上・1以下の値になり、値の目安として以下のような基準が設けられています。
| 相関係数の絶対値 | 目安 |
|---|---|
| 0 ~ 0.2 | ほとんど無相関 |
| 0.2 ~ 0.4 | 弱い相関 |
| 0.4 ~ 0.7 | 中程度の相関 |
| 0.7 ~ 1 | 強い相関 |
散布図とともに相関係数を確認しましょう。
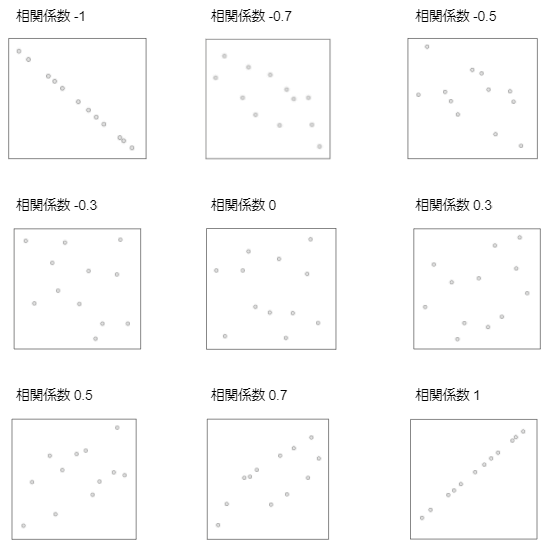
引用:https://data-viz-lab.com/correlation-coefficient
相関係数が利用できない場面
相関係数が計算できない、あるいは計算してもあまり意味のない場合の例について紹介します。
実際に利用するときは、下記の場合に注意しましょう。
直線的でない関係の場合
「相関係数」とは、2つの変数の間に直線関係に近い傾向が見られるか数値で表したものであるため、その他の関係を捉えることはできません。
データ数が少ない場合
データ数が少ない場合、相関係数の誤差は大きくなってしまいます。
十分な量のデータがあるか確認しましょう。
外れ値がある場合
前述で紹介した相関係数は、正しくは「ピアソンの(積率)相関係数」といいます。
ピアソンの相関係数は外れ値に大きな影響を受けるので注意が必要です。
外れ値がある場合は、「スピアマンの順位相関係数」や「ケンドールの順位相関係数」といった相関係数を用いると良いでしょう。
平均や分散が発散する分布の場合
データの集め方によって結果が大きく異なる傾向にあります。
相関関係と因果関係
まず、因果関係の定義について確認します。
因果関係の定義は、「原因とそれによって生じる結果との関係」です。
相関関係と因果関係を簡単に比較すると
- 相関関係:XとYに直線的な関係がある
- 因果関係:XによってYが決まる
となります。
「XによってYが決まる」というのも一つの関係なので、因果関係ならば相関関係となります。
一方、相関関係ならば因果関係は必ずしも成り立つとは限りません。
相関関係はあるが、因果関係ではない例は下記のようなものがあります。

相関関係は定義式通りに相関係数を計算するだけで確かめることができました。
一方、因果関係を判定するのは、上記の例のように様々な要因が複雑に絡み合っている可能性があるため非常に難しいです。
因果関係を証明したい場合は
- ランダム化比較実験
- 傾向スコア分析
と呼ばれる手法を利用します。
興味がある方はぜひ調べてみてください。
最後に、下の図で「相関と因果」の関係を確認しましょう。
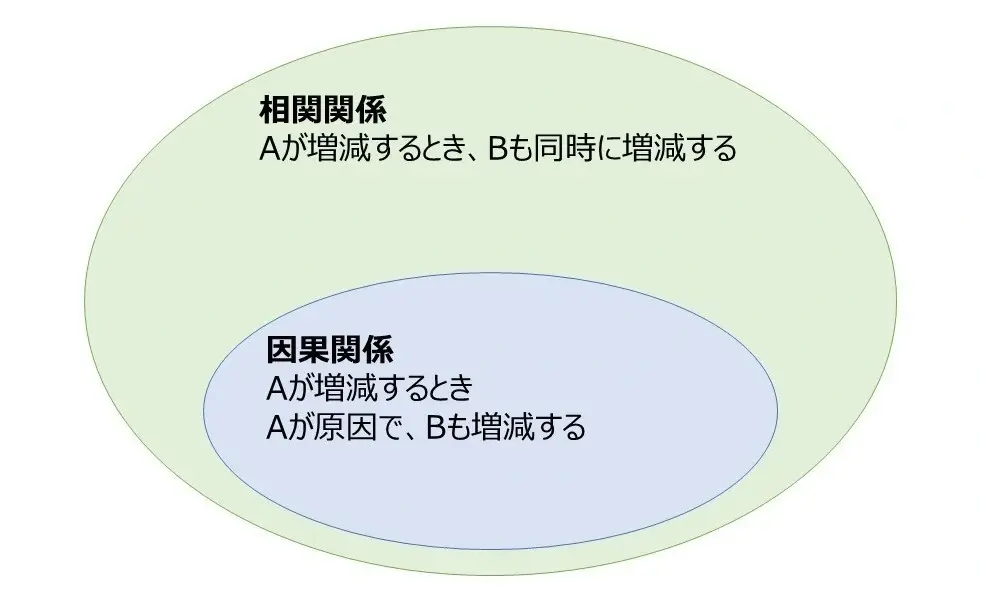
引用:https://www.bewith.net/gemba-driven/article/digital/entry-242.html
擬似相関と編相関係数
擬似相関(見かけの相関)とは
擬似相関とは、対象となる2つの変数と強い相関を持つ第3の変数(共通原因)を間に挟んだ際にみられる相関を意味します。
下記の具体的な問題で、擬似相関の理解を深めましょう。
小学生の「テストの点数」のデータと「身長」のデータから相関係数を求めたところ、相関があることが得られたとします。
この場合、「身長が大きい(体の成長が早い)と頭が良い」と言えるでしょうか?
解答:答えは「No」です。
なぜなら小学生の場合、学年が上がるほど身長も大きくなり、算数の点数も上がる傾向にあるからです。
すなわち
- 学年 → 身長
- 学年 → 算数の点数
と第3の変数の影響により、「身長」と「算数の点数」の間に強い相関関係があるように見えてしまいました。
この場合、「身長」と「算数の点数」の間に擬似相関(見かけの相関)があると言います。
次に発展的な内容として「身長」と「算数の点数」の関係において、「学年」の影響を除いた相関係数を求めたいと思います。
編相関係数の求め方
編相関係数とは、3つの変数があるとき第3の変数の影響を除いた相関係数です。
X,Y,Zの変数の内、Zの影響を除いた編相関係数は以下のように定義されています。
\[
r_{XY \cdot Z} = \frac{\scriptsize r_{XY} – \scriptsize r_{XZ} \cdot \scriptsize r_{YZ}}{\sqrt{(\scriptsize 1 – \scriptsize r_{XZ}^2) \cdot (\scriptsize 1 – \scriptsize r_{YZ}^2})}
\]
$$
r_{XY}:\text{XとYの相関係数}\\
r_{XZ}:\text{XとZの相関係数}\\
r_{YZ}:\text{YとZの相関係数}\\
$$
下記の練習問題で編相関係数を求めてみましょう。
練習問題
小学生のデータにおいて、3つの変数間で以下のような相関係数が得られたする。
- 「算数の点数」と「身長」:r = 0.935
- 「算数の点数」と「学年」:r = 0.815
- 「身長」と「学年」:r = 0.792
このとき、「学年」の影響を除いた編相関係数を求めよ。
X、Yを「算数の点数」、「身長」とし、Zを「学年」とする。
定義式
\[
r_{XY \cdot Z} = \frac{\scriptsize r_{XY} – \scriptsize r_{XZ} \cdot \scriptsize r_{YZ}}{\sqrt{(\scriptsize 1 – \scriptsize r_{XZ}^2) \cdot (\scriptsize 1 – \scriptsize r_{YZ}^2})}
\]
より
$$ r_{XY \cdot Z} \simeq \scriptsize 0.146 $$
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
コラム:指標に隠された罠
前章の「平均・分散とは?基本統計量を分かりやすく解説!」と本章で、平均や分散・相関係数など様々な指標を確認しました。
指標はデータの特性を数値で解析できるため非常に便利なことは間違いありません。
しかし、データを数値だけで判断しないで、グラフで視覚的に確認することも非常に大切です。
以下のグラフは「x,yの平均、分散、相関係数が全て同じ」です。
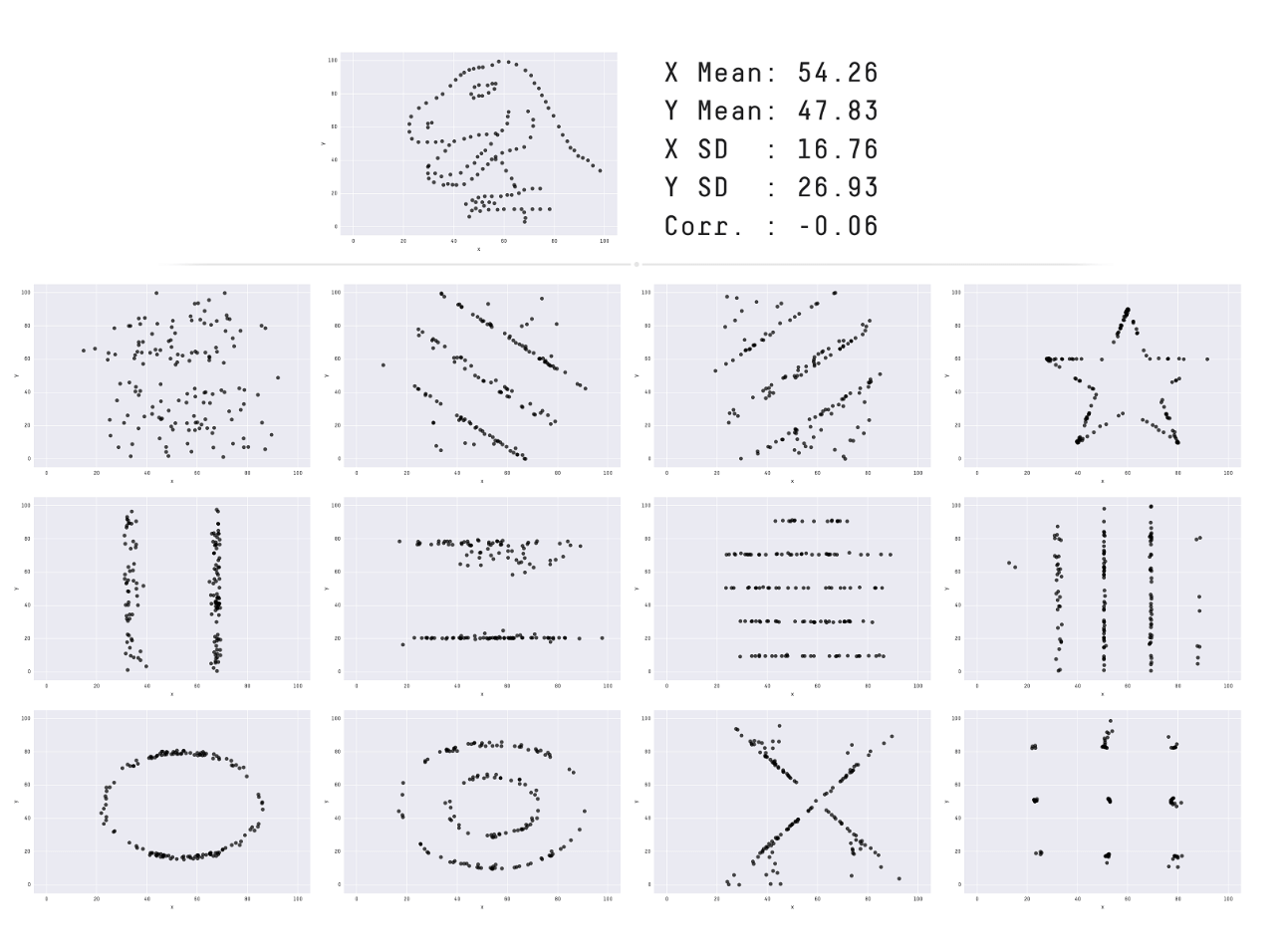
引用:Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing
このように指標は全く同じでも、グラフの概形は異なる場合もあるので視覚による解析も忘れないようにしましょう。










