
本連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
第3章では、「確率の基本」について解説します。
統計学を学ぶ上で「確率」は避けては通れない学問なので、この章で確率の基本をマスターしましょう。
また、コラムでは「イメージと異なる確率」として、私たちの感覚と実際に求めた確率が異なる例について紹介します。
ぜひ、最後までご覧ください。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章:平均・分散などの基本統計量
2章:相関関係
3章:確率の基本
4章:条件付き確率・ベイズの定理
5章:期待値
6章:代表的な確率分布
7章:母集団と標本
8章:標本平均・不偏分散
9章:中心極限定理
10章:母平均の推定(分散既知)
11章:母平均の推定(分散未知)
12章:仮説検定
13章:正規分布を用いた検定
14章:【t検定】母平均を検定
15章:【F検定】分散に差があるか?
16章:ウェルチの検定
17章:カイ2乗検定
18章:分散分析
19章:回帰分析
確率とは
確率の定義
確率とは、ある物事が起こる可能性の度合いを数値で表したものです。
以下の式で確率を求めることができます。

試行とは、ある実験やイベントの一回の実施を指します。
- コインを投げること
- サイコロを振ること
- カードを引くこと
などが試行の例です。
事象とは、試行において発生する可能性のある結果や出来事のことを指します。
- コインを投げた場合の表が出ること
- サイコロを振った場合の特定の目が出ること
- カードを引いた場合の特定のスートや数字が出ること
などが事象の例です。
この場合の数は、同様に確からしい事象を数えなければなりません。
「同様に確からしい」とは、「起こる可能性が同様である」ということです。
例えば、「サイコロを振った時に出る目」は同様に確からしいものとして扱われます。
一方、宝くじで当たる確率について考えます。
全事象は「当たる場合」と「外れる場合」の2通りでありますが、
$$ \frac{\scriptsize 1}{\scriptsize 2} $$
とは言えません。
これは「当たる場合」と「外れる場合」が同様に確からしくないからです。
下記の練習問題で実際に確率を求めてみましょう。
練習問題
6面のサイコロを1回振った時、偶数の目が出る確率を求めよ。
ただし出る目は同様に確からしいとする。
「偶数の目が出る」という事象を事象Aとします。
サイコロの出る目は「1」、「2」、「3」、「4」、「5」、「6」であり、同様に確からしいです。
この内、偶数は「2」、「4」、「6」です。
したがって
- 全ての場合の数:6通り
- 事象Aが起こる場合の数:3通り
以上より求める確率pは、
$$ p = \frac{\scriptsize 3}{\scriptsize 6} = \frac{\scriptsize 1}{\scriptsize 2} $$
事象の演算
確率を考える際には、複数の事象を考慮する必要がある場合もあります、
そのため、確率を学ぶ上で不可欠な基本的な「事象の演算」について解説いたします。
なお、以下では全体集合を「Ω」とします。
和事象
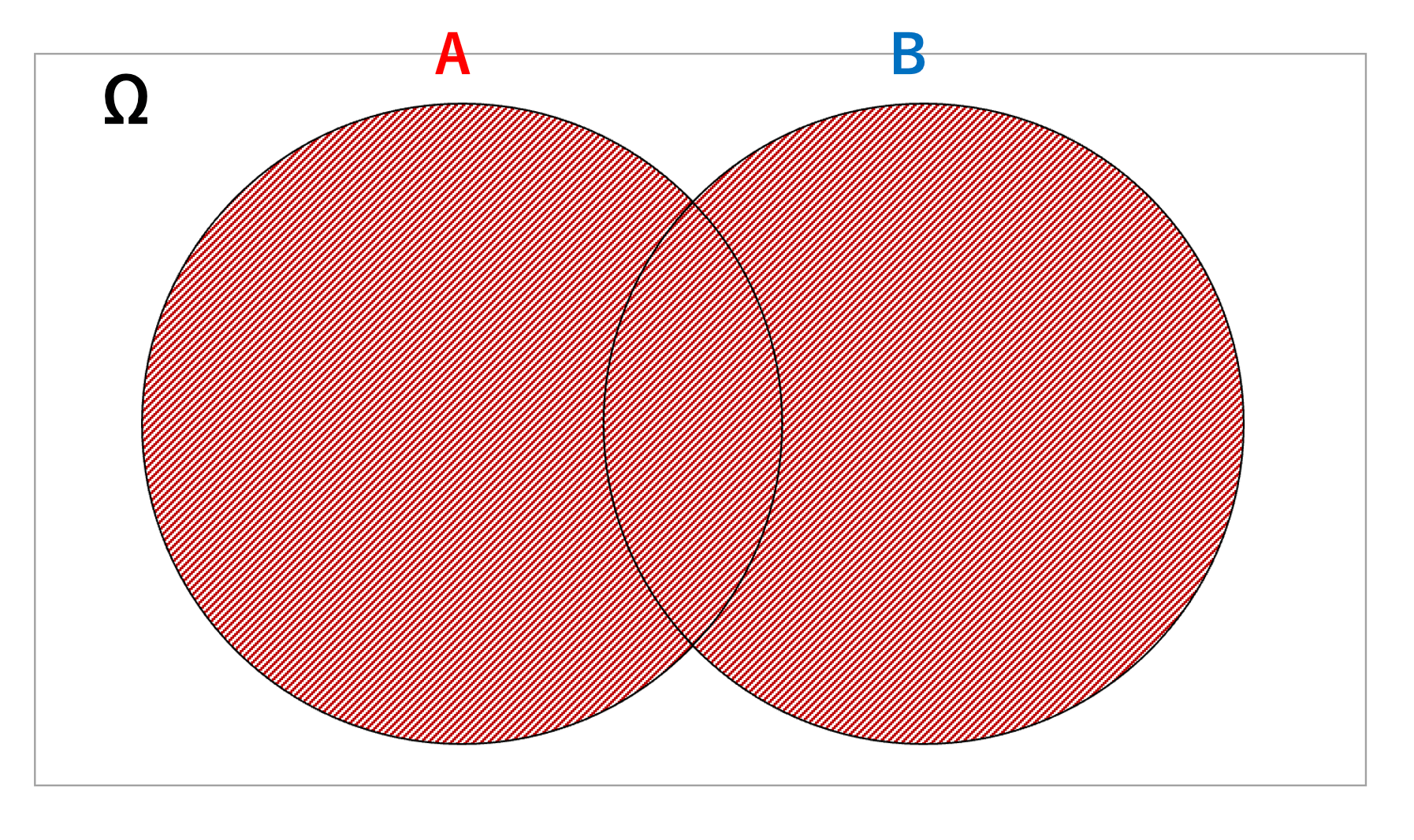
AとBの和事象とは、「AまたはBが起こる」という事象です。
AとBの和事象は以下のように表されます。
$$ A\cup B $$
下記の画像で和事象のイメージを掴んでおきましょう。
積事象
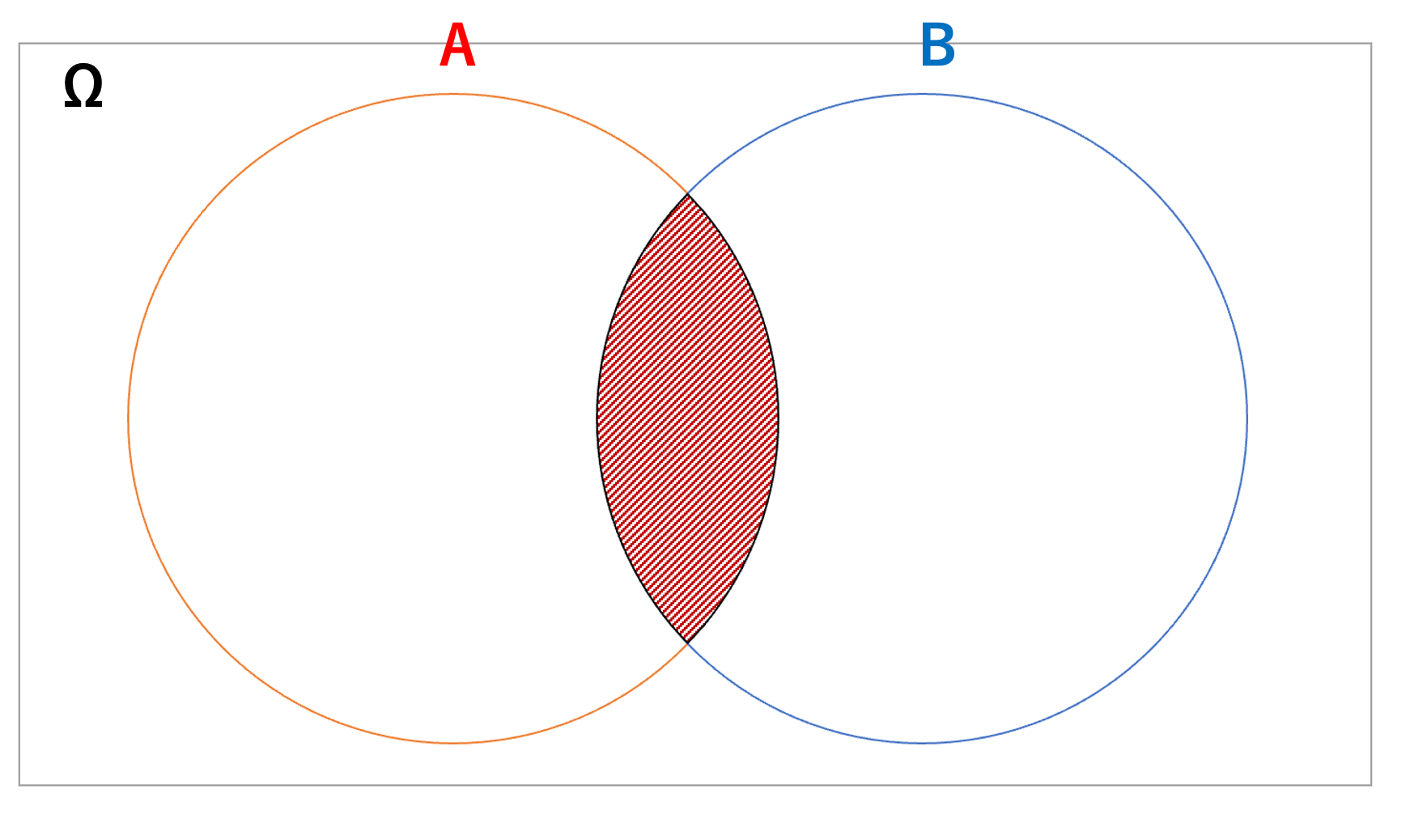
AとBの積事象とは、「AかつBが起こる」という事象です。
AとBの和事象は以下のように表されます。
$$ A\cap B $$
下記の画像で積事象のイメージを掴んでおきましょう。
余事象
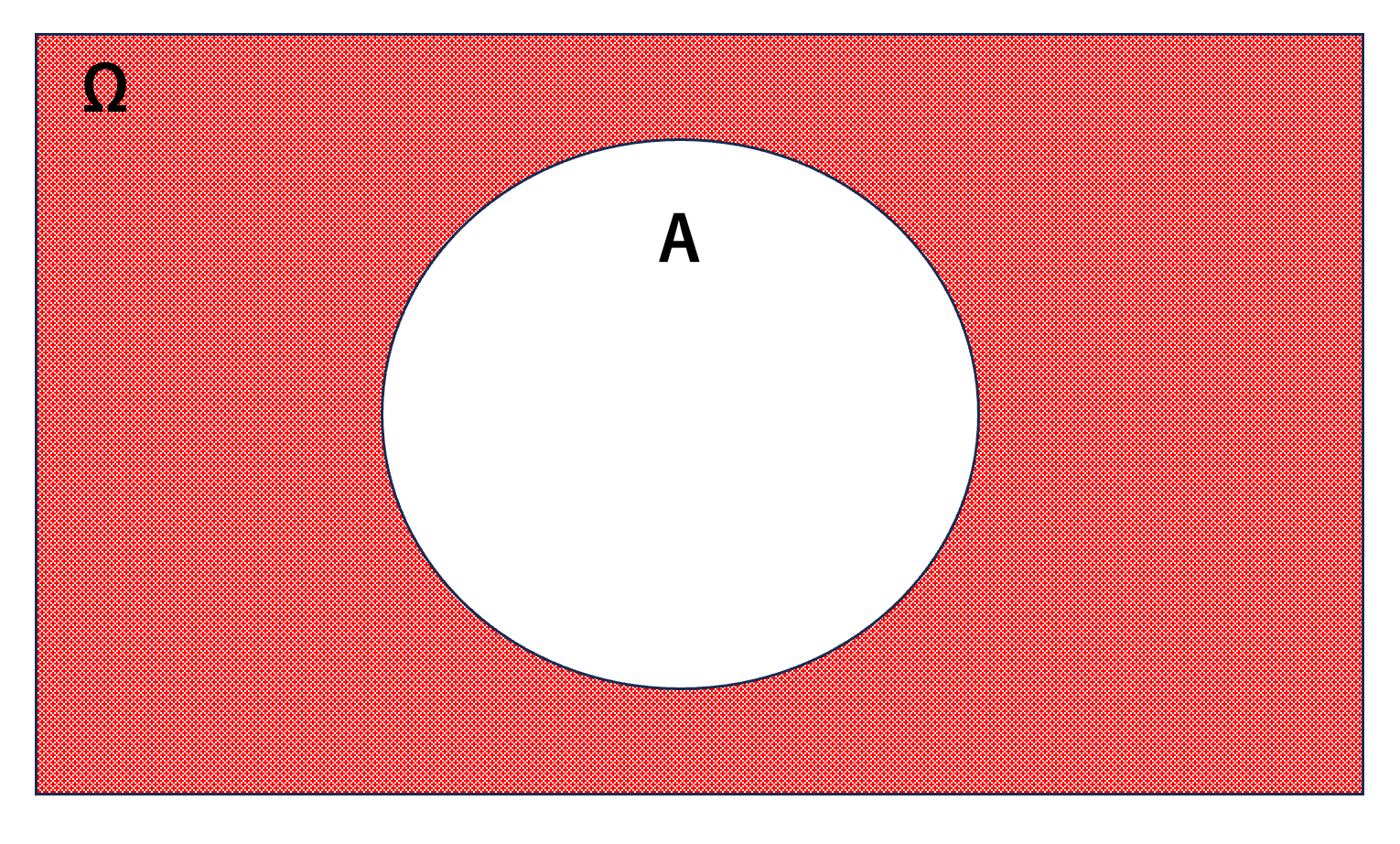
Aの余事象とは、「Aが起こらない」という事象です。
Aの余事象は以下の2通りで表されます。
$$ A^c 、\bar{A} $$
下記の画像で余事象のイメージを掴んでおきましょう。
排反な事象
排反な事象とは、「一方の事象が起きた時、他方の事象が起きない」事象のことを言います。
例えばコインを一回投げた場合、
- コインの表が出る事象
- コインの裏が出る事象
は同時に起きません。
このような事象を「排反である」と言います。
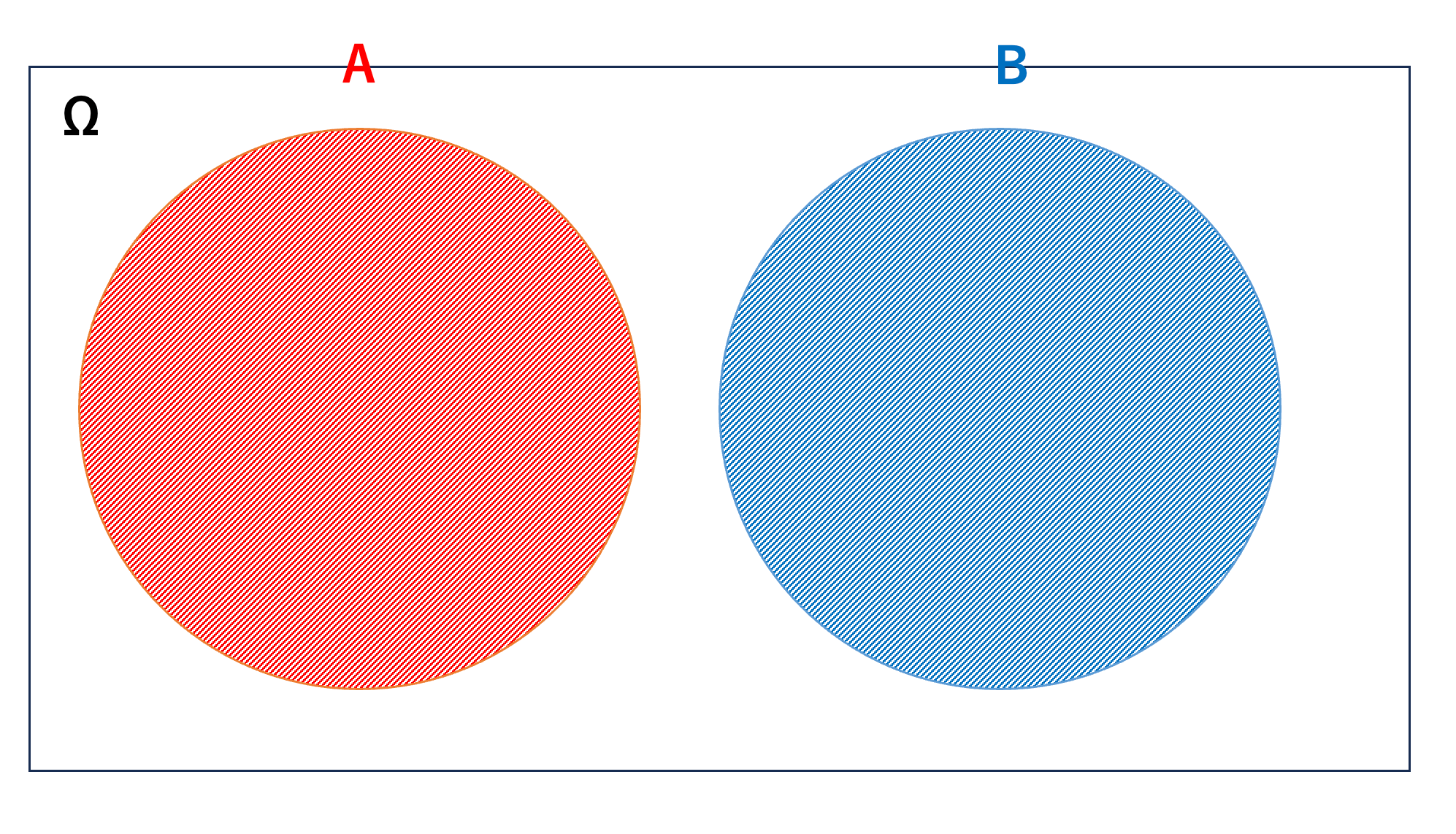
排反な事象は、下記のようにも表現できます。
$$ A\cap B = \phi $$
φは空事象(存在しない事象)を表します。
下記の画像で排反な事象のイメージを掴んでおきましょう。
場合の数の求め方・計算
効率的に場合の数を求める方法を解説します。
下記で解説する内容は基本的な内容であると共に、マスターすると多くの場面の「場合の数・確率」を計算できるようになります。
樹形図
場合の数を考える上で最も大切なものが「樹形図」です。
樹形図とは、「どんな場合が考えられるか考えるために用いる、木構造で表現された図」です。
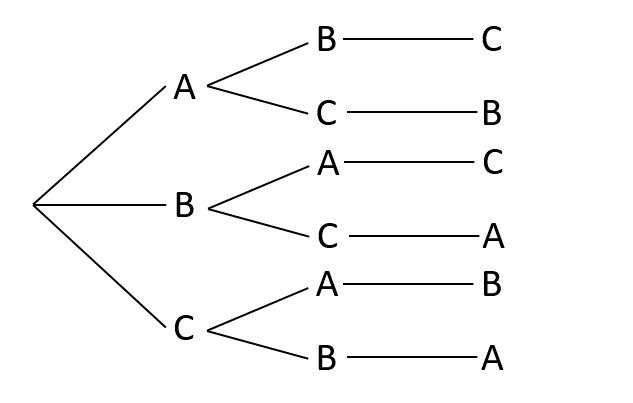
場合の数を学ぶと様々な公式が登場しますが、樹形図が元となって導出されたものが多くあります。
順列
順列とは、「異なるn個からr個選んで1列に並べる時の場合の数」を意味します。
そして順列は以下の式で求めることができます。
$$ {}_n P_r = n \times (n – 1) \times \dots \times (n – r + 1) $$
式を見て理解するのは難しいと思うので、下記の「ポイント」の方法で計算しましょう。
nから始めて「1」ずつ減らしたものをr個掛ける。
例として「A、B、C、Dの4人から2人を選んで一列に並べる」という状況を考えます。
$$ {}_4 P_2 = 4 \times 3 $$
このように「4」→「3」と4(n)から「1」ずつ減らして、2(r)個掛けると順列を計算できます。
この問題を樹形図を用いて考えると下記のようになります。
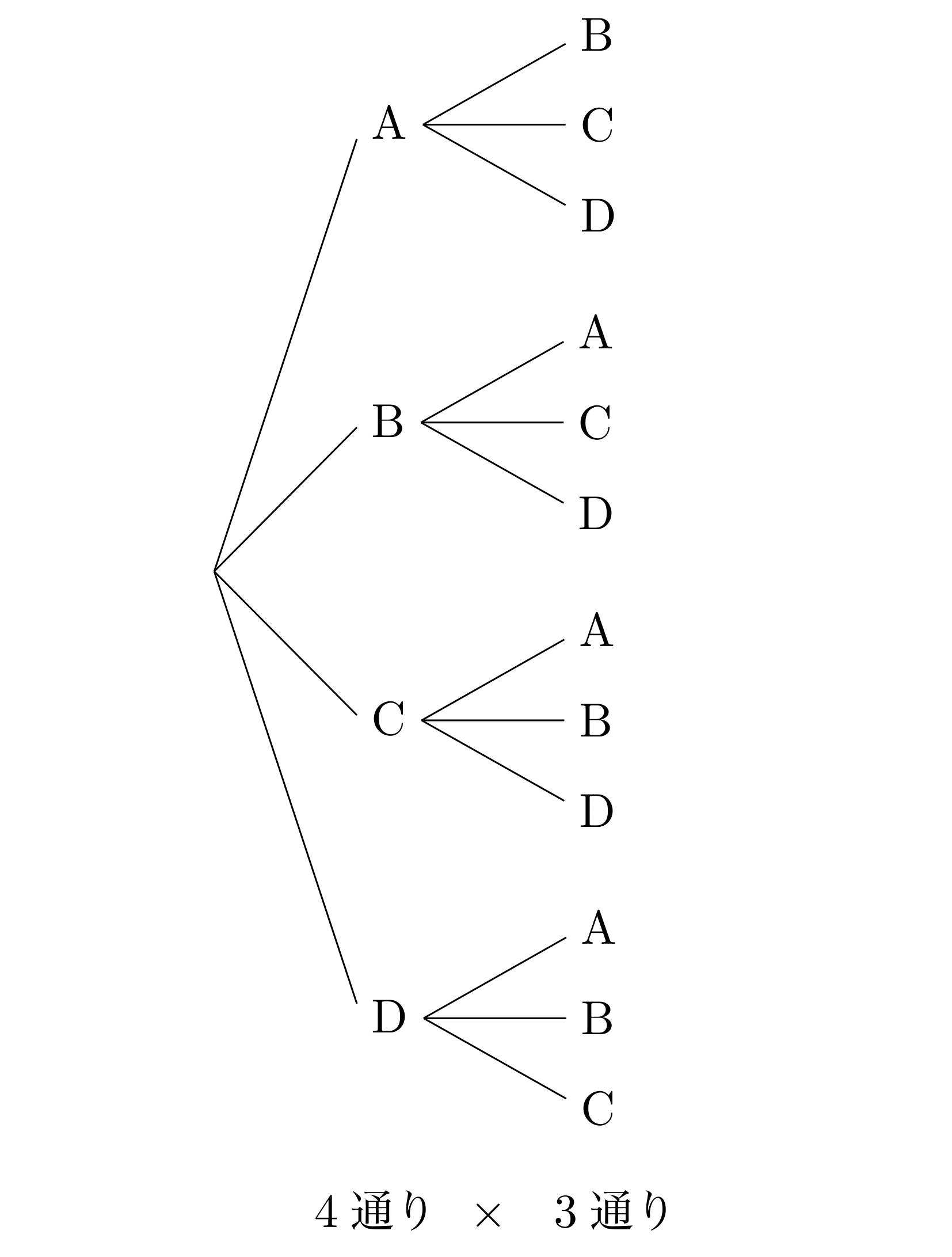
この順列は樹形図からも分かるように
- 1人目は「A ~ D」の4通り
- 2人目は「1人目で選んだ人以外」の3通り
と計算しています。
次に下記のような問題を考えます。
問題
3人を1列に並べる場合の数を求めよ。
解答
順列の定義より下記の式で計算できる。
$$ {}_3 P_3 = \scriptsize 3 \times \scriptsize 2 \times \scriptsize1 $$
このように「異なるn個からn個選んで1列に並べる時の場合の数」を特に「階乗」と言い、下記のように表現します。
$$ {}_n P_n = n! $$
「nのカイジョウ」と読みます。
今回の問題では「3!」と書きます。
組み合わせ
組み合わせとは、「異なるn個からr個選ぶ場合の数」を意味します。
順列との違いは、 「組み合わせ」は1列に並べないという点です。
そして組み合わせは以下の式で求めることができます。
$$ {}_n C_r = \frac{{}_n P_r}{r!} $$
問題
A、B、C、Dの4人から2人選ぶ場合の数を求めよ。
組み合わせの定義通りに計算すると、
\[ {}_4 C_2 = \frac{{{}_4 P_2}}{{\scriptsize 2!}} = \frac{{\scriptsize 4 \times \scriptsize 3}}{{\scriptsize 2 \times \scriptsize 1}} = \scriptsize 6 \]
次に「組み合わせの式」についてより理解するために別の解き方を考えます。
A、B、C、Dの4人から2人選ぶ場合の数をxとする。
「A、B、C、Dの4人から2人選んで一列に並べる場合の数」は「A、B、C、Dの4人から2人選んで、その2人を並べる場合の数」と同値です。
したがって、
$$\begin{align*} x \times \scriptsize 2! &= {}_4 P_2 \\ x &= \frac{{{}_4 P_2}}{{\scriptsize 2!}} \end{align*}$$
このように、「順列」→「組み合わせ」と考えることで、「組み合わせ」の定義式も理解できます。
「順列」と「組み合わせ」の違い
順列と組み合わせの違いは、「1列に並べるか」ですが、実際には臨機応変に対応しなければなりません。
以下の問題を考えてみましょう。
問題
30人のクラスで委員長、副委員長、書記を決める。
この選び方は何通りあるか?
上記の問題を解くとき、用いるのは「順列P」と「組み合わせC」のどちらでしょうか?
正解は「順列P」です。
なぜなら「委員長、副委員長、書記を前から順に並べる」と考えれば、「1列に並べる」という問題に置き換えることができるからです。
したがって、順列と組み合わせの違いは「一列に並べる問題に置き換えられるか」ということになります。
「確率」練習問題
上記で学んだ確率の求め方や場合の数の計算方法を利用して、下記の問題を考えてみましょう。
問題1
「1」「2」「3」「4」と書かれた4枚のカードから3枚選んで、3桁の数字を作る。
作られた数字が偶数となる確率を求めよ。
まず、「4枚のカードから3枚選んで、3桁の数字を作る」場合の数を考えます。
「4枚のカードから3枚選んで、3桁の数字を作る」は「数字を百の位から1列に並べる」という問題に置き換えられます。
そのため、この問題では「順列(P)」を用います。
よって以下のように求められます。
$$ {}_4 P_3 = \scriptsize 4 \times \scriptsize 3 \times \scriptsize 2 = \scriptsize 12 $$
次に、「4枚のカードから3枚選んで、3桁の偶数の数字を作る」場合の数を考えます。
偶数となるのは「1の位が偶数」の時です。
そのため、一の位は「2」と「4」の2通りです。
次に百の位、十の位の場合の数を考えます。
1の位で用いた数字を除いた3つの数字から2つの数字を選んで1列に並べるため、
$$ {}_3 P_2 = \scriptsize 3 \times \scriptsize 2 = \scriptsize 6 $$
以上から「4枚のカードから3枚選んで、3桁の偶数の数字を作る」場合の数は
$$ \scriptsize 6 \times \scriptsize 2 = \scriptsize 12 $$
よって求める確率は
$$ \frac{\scriptsize 12}{\scriptsize 24} = \frac{\scriptsize 1}{\scriptsize 2} $$
問題2
白いボール2個と赤いボール3個があります。
この中から無作為にボールを2つ取り出すとき、赤いボールが少なくとも1つ取り出される確率はいくらでしょうか。
この問題2は「1列に並べる」という問題に置き換えることができないため「組みわせ(C)」を用います。
5つのボールから無作為にボールを2つ取り出す場合の数は
$$ {}_5 C_2 = \frac{{}_5 P_2}{\scriptsize 2!} = \scriptsize 10 $$
「少なくとも~である」は、確率全体から「1回も出ない」を引く と「少なくとも1回は出る確率」を求めることができます。

赤玉が1つも取り出されない場合の数は
$$ {}_2 C_2 = \frac{{}_2 P_2}{\scriptsize 2!} = \scriptsize 1 $$
よって赤玉が1つも取り出されない確率は
$$ \frac{\scriptsize 1}{\scriptsize 10} $$
したがって、求める確率は
$$ \scriptsize 1 – \frac{\scriptsize 1}{\scriptsize 10} = \frac{\scriptsize 9}{\scriptsize 10} $$
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
コラム:イメージと異なる確率
ガチャは思ったより当たらない?
スマートフォのゲーム「ガチャ」などで以下のような経験をした方も多いのではないでしょうか?
1%のガチャを100回引いたのに当たらなかった
そこで今回は以下の問題について考えてみます。
あるガチャで、レアアイテムを引き当てる確率が1%だったとします。
100回引けばどのくらいの確率で、少なくとも1回レアアイテムを引き当てられるでしょうか?
なお、ガチャで引いたもの除外しないものとします。
感覚的に「結構な確率でレアアイテムを引き当てられる」と考えている方も多いと思います。
実際に計算して確かめてみましょう。
一回ガチャを引いて、レアアイテムを引けない確率は
$$ \scriptsize 0.99 $$
そのため、100回連続レアアイテムを引けない確率は
$$ (\scriptsize 0.99)^{\scriptsize 100} $$
したがって、少なくとも1回レアアイテムを引き当てられる確率は
$$ \scriptsize 1 – ( \scriptsize 0.99)^{\scriptsize 100} \approx \scriptsize 0.63 $$
したがって、100回引いて出現確率1%のアイテムが当たる確率は約63%です。
「想像していた確率よりも低い!」と感じたのではないでしょうか?
このように私たちが感覚的に持っている確率と実際に計算した確率が異なることは多々あります。
確率を勉強することで、数値データに騙されにくくなったり、良い意思決定を下すのに役立ったりするでしょう。









