連載講座「0から学ぶ確率統計」では、中学数学の基本的な内容から大学レベルの確率統計を解説しています。
統計やデータサイエンスに興味がある方はぜひご覧ください。
前章までは確率論をメインに学習してきましたが、本章から本格的に統計学の内容に入っていきます。
第7章では、「統計の基本用語」について解説します。
「母集団」や「推測統計学」、「区間推定」など統計において頻繁に登場する用語をわかりやすく解説しています。
本連載講座「0から始める確率・統計講座」では、中学・高校レベルの数学から大学レベルの「確率・統計」を解説しています。
確率・統計を始めて学ぶ方が理解できるよう、丁寧に解説しています。
この講座の内容は「統計検定2級レベルの知識を習得すること」を目標としています。
・中学、高校の数学の内容を覚えてないけど
「確率・統計」を学習したい
・統計検定の対策をしたい
このような考えを持っている方は、Tech Teacherが運営する「0から始める確率・統計講座」を用いて、「確率・統計」の学習をすすめましょう。
<目次>
1章：平均・分散などの基本統計量
2章：相関関係
3章：確率の基本
4章：条件付き確率・ベイズの定理
5章：期待値
6章：代表的な確率分布
7章：母集団と標本
8章：標本平均・不偏分散
9章：中心極限定理
10章：母平均の推定(分散既知)
11章：母平均の推定(分散未知)
12章：仮説検定
13章：正規分布を用いた検定
14章：【t検定】母平均を検定
15章：【F検定】分散に差があるか？
16章：ウェルチの検定
17章：カイ2乗検定
18章：分散分析
19章：回帰分析
本ブログを運営しているTech Teacherは、
プログラミング家庭教師サービスを運営しています。
完全マンツーマン・フルオーダーメイドで
あなたが必要な指導を提供します。
母集団と標本
「母集団」と「標本」の関係を下の図でまとめました。
単語の意味について確認する前に、それぞれの関係のイメージを掴んでおきましょう。
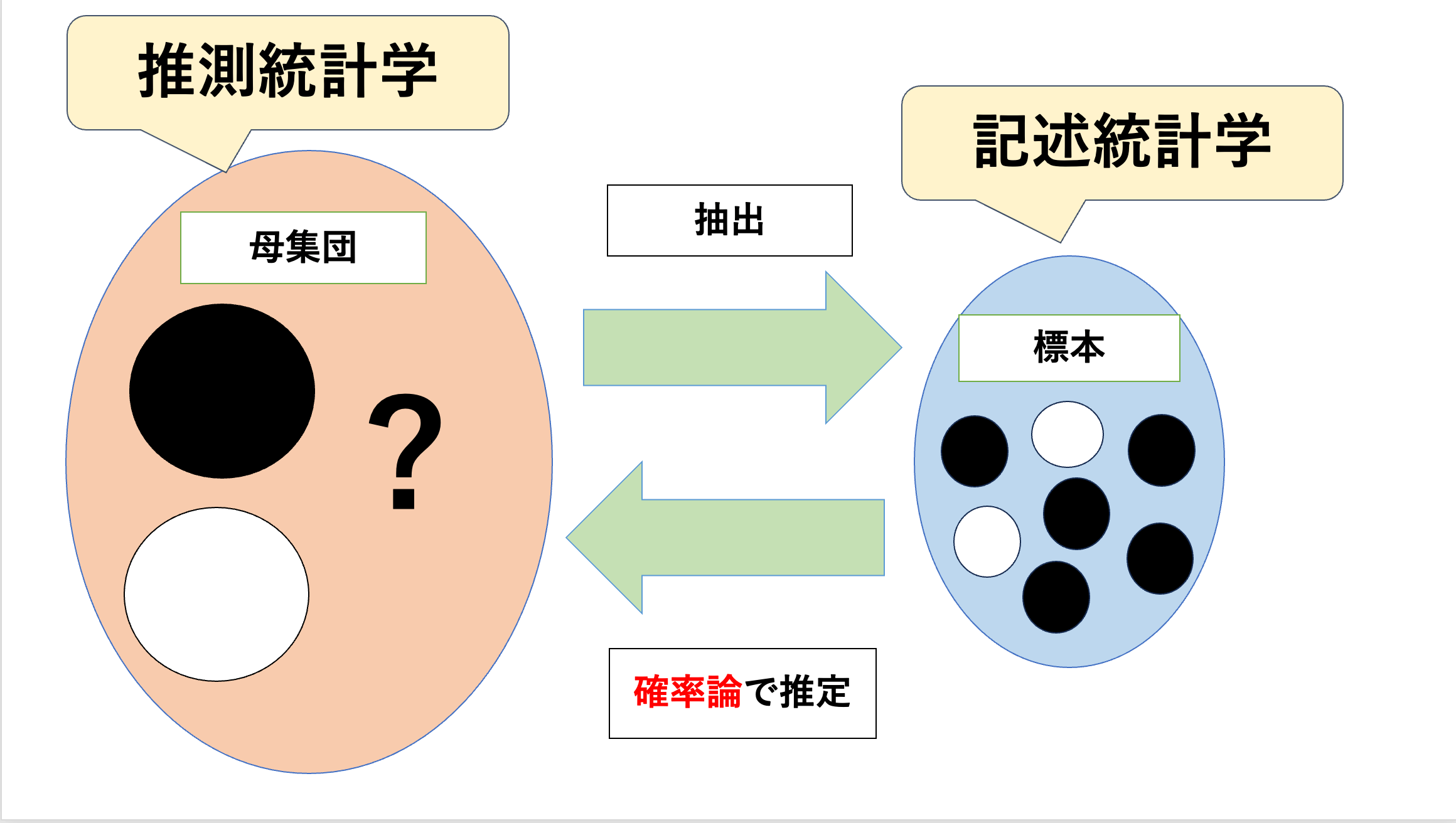
母集団とは、知りたいと思う集団全体を意味します。
例えば、「全国民の身長」を調査する場合、全国民が母集団となります。
分析をする際に、もし母集団全体を調査できれば、正確な情報を取得することができます。
しかし、母集団は通常非常に広範であり、その全体を調査することは一般的に難しいです。
そこで、次に紹介する「標本」を利用して分析を行います。
標本
標本とは、母集団から分析のために選びだされた要素の集団を意味します。
先ほどの例の「全国民の身長」を調査する場合、国民全員を調査することは困難なため、ランダムに選ばれた国民を対象にデータを収集します。
母集団から標本を抽出するときは、無作為に抽出することが大切です。
例えば「全国民の身長」の調査で、被験者の年齢が偏って18歳以上の人しか選んでいなかったり、性別が男性に偏っていたりすると、身長が大きく見積もられ、正しく母集団の性質を反映できなくなってしまいます。
推測統計学
推測統計学とは、収集した一部のデータ(標本)から全体(母集団)の性質や傾向を推測することを意味します。
例えば「全国民の身長」を調査する場合、無作為に1万人ほどの人を選んで身長を測定したとします。
この1万人のデータから、「全国民の身長の平均や分散はどの程度であるか」を確率論を用いて推定するのが推測統計学です。
次の章以降では、この推測統計学について学習していきます。
なお、確率論と聞くと難しいイメージがありますが、本連載講座の推測統計学で必要な知識は「平均や分散、正規分布」といった基本的な内容なのでご安心ください。
「平均や分散、正規分布」が分からない方は、以前の章で丁寧に解説しているのでぜひそちらをご覧ください。
1章：平均・分散などの基本統計量
2章：相関関係
3章：確率の基本
4章：条件付き確率・ベイズの定理
5章：期待値
6章：代表的な確率分布
記述統計学
記述統計学とは、集団の特徴を記述するために、データを集め、得られたデータを整理・要約する方法を意味します。
推測統計学との違いは、推測統計学は母集団を調査対象にしていましたが、記述統計学では集めたデータ(標本)を調査対象にしている点です。
例えば、国勢調査は全国民を対象としデータを集めているので、すべてのデータを把握して用いる記述統計の一例です。
記述統計学では、国勢調査などデータが膨大な場合、データを集めても解釈するのが難しいため、平均や分散を求めたり、グラフで可視化したりしています。
記述統計の分析ツールとして、「Excel」が用いられることが多いです。
本記事を運営する「Tech Teacher」では、Excel未経験の方、自身の無い方でも順を追って学習できる【Excelによる統計解析講座】を用意しているので併せてご覧ください。
『Tech Teacher』3つの魅力
魅力1. オーダーメイドのカリキュラム
『Tech Teacher』では、決められたカリキュラムがなくオーダーメイドでカリキュラムを組んでいます。「質問だけしたい」「相談相手が欲しい」等のご要望も実現できます。
魅力2. 担当教師によるマンツーマン指導
Tech Teacherでは、完全マンツーマン指導で目標達成までサポートします。
東京大学を始めとする難関大学の理系学生・院生・博士の教師がが1対1で、丁寧に指導しています。
そのため、理解できない箇所は何度も分かるまで説明を受けることができます。
魅力3. 3,960円/30分で必要な分だけ受講
Tech Teacherでは、授業を受けた分だけ後払いの「従量課金制」を採用しているので、必要な分だけ授業を受講することができます。また、初期費用は入会金22,000円のみです。一般的なプログラミングスクールとは異なり、多額な初期費用がかからないため、気軽に学習を始めることができます。
まとめ
・魅力1. 担当教師によるマンツーマン指導
・魅力2. オーダーメイドのカリキュラム
・魅力3. 3,960円/30分で必要な分だけ受講
質問のみのお問い合わせも受け付けております。
推定
次に母集団の平均や分散といった値を、標本から推測する手法の概要について紹介します。
推定手法には「点推定」と「区間推定」があります。
それぞれの推定の特徴について確認していきましょう。
点推定
点推定とは、母数「\(\theta \)」をただ一つの値「\(\widehat{\theta} \)」で推定する手法を指します。
「母数」とは、母集団の性質を表す統計量のことです。
例えば、「母平均」や「母集団」が挙げられます。
例えば、ある県知事の本来の支持率を「p」、推定された支持率を「\(\widehat{p}\)」とします。
数百人をインタビューした結果、支持率が「0.60」とします。
このとき、県全体での支持率
$$ \widehat{p} ＝ \scriptsize 0.60 $$
と値を1点のみで推定するのが点推定です。
点推定の主な推定方法として、
- 最尤法
- モーメント法
があります。
区間推定
母数を、1つの値ではなく、入る区間（幅）で推定します。
点推定では、ただ一つの値で推定しましたが、あくまでも推定なので実際にはズレが存在します。
そのため、区間推定では、母数が「90%や95%などのある程度高い確率で存在する区間」を推定することを目的にしています。
先ほどの例と同様に、ある県知事の本来の支持率を数百人にインタビューした結果、支持率が「0.60」であったとします。
本当の支持率は「0.50」であるのに、インタビューした人は賛成寄りが多く、支持率が「0.60」となっている場合もあります。
区間推定では、本当の支持率が95%の確率で的中する区間を求めるという、確率的なズレを組み込んだ推定を行います。
例えば値のイメージとして、支持率は「0.40 ~ 0.80」である確率が95%であるという風に推定します。
